
Достаточные условия существования локальных экстремумов
Пусть функция
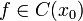 непрерывна
в
непрерывна
в  и
существуют конечные или бесконечные
односторонние производные
и
существуют конечные или бесконечные
односторонние производные  .
Тогда при условии
.
Тогда при условии
![]()
x0 является точкой строгого локального максимума. А если
![]()
то x0 является точкой строгого локального минимума.
Заметим, что при этом функция не дифференцируема в точке x0
Пусть функция f непрерывна и дважды дифференцируема в точке x0. Тогда при условии
![]() и
и ![]()
x0 является точкой локального максимума. А если
и ![]()
то x0 является точкой локального минимума.
ВОПРОС№27: Основные теоремы о дифференцируемых функциях.
Дифференци́руемая фу́нкция—это функция, имеющая дифференциал (линейная часть приращения функции.) . Дифференцируемая функция может быть хорошо приближена линейной функцией. Дифференцируемость является одним из фундаментальных понятий в математике и имеет большое число приложений как внутри неё, так и в естественных науках, широко использующих математический аппарат (на данном отрезке). 1.Теорема Ро́лля (теорема о нуле производной) утверждает, что Если вещественная функция непрерывна на отрезке [a;b] и дифференцируема на интервале (a;b) , принимает на концах этого интервала одинаковые значения, то на этом интервале найдётся хотя бы одна точка, в которой производная функции равна нулю. 2.Теорема Лагранжа Если функция f: [a, b] → R непрерывна на сегменте [a, b] и имеет конечную или бесконечную производную во внутренних точках этого сегмента, то такое, что f(b) - f(a) = f'(ξ)(b - a). 3.Теорема Коши Если каждая из функций f и g непрерывна на [a, b] и имеет конечную или бесконечную производную на ]a, b[ и если, кроме того, производная g'(x) ≠ 0 на ]a, b[, то такое, что справедлива формула Если дополнительно потребовать, чтобы g(a) ≠ g(b), то условие g'(x) ≠ 0 можно заменить менее жестким.
ВОПРОС№30: Точки перегиба и способы их нахождения.
Точка
![]() называется точкой
перегиба
графика функции y = f(x), если в данной
точке существует касательная к графику
функции (она может быть параллельна оси
Оу) и существует такая окрестность точки
, в пределах которой слева и справа от
точки М график функции имеет разные
направления выпуклости.
называется точкой
перегиба
графика функции y = f(x), если в данной
точке существует касательная к графику
функции (она может быть параллельна оси
Оу) и существует такая окрестность точки
, в пределах которой слева и справа от
точки М график функции имеет разные
направления выпуклости.
Другими словами, точка М называется точкой перегиба графика функции, если в этой точке существует касательная и график функции меняет направление выпуклости, проходя через нее.
необходимое
условие перегиба.1.Пусть
график функции y = f(x) имеет перегиб в
точке
и имеет при
![]() непрерывную вторую производную, тогда
выполняется равенство
непрерывную вторую производную, тогда
выполняется равенство
![]() .
.
2.абсциссами
точек перегиба могут быть все
![]() из области определения функции, для
которых
из области определения функции, для
которых![]() и
и![]()
Алгоритм нахождения точек перегиба функции.Находим все абсциссы возможных точек перегиба графика функции ( или и ) и выясняем, проходя через какие вторая производная меняет знак. Такие значения и будут абсциссами точек перегиба, а соответствующие им точки будут точками перегиба графика функции. Алгоритм нахождения точек перегиба функции.
ВОПРОС№31: Формула Тейлора. Разложение некоторых элементарных функций по формуле Тейлора.
Теорема Тейлора. 1) Пусть функция f(x) имеет в точке х = а и некоторой ее окрестности производные порядка до (n+1) включительно.{ Т.е. и все предыдущие до порядка n функции и их производные непрерывны и дифференцируемы в этой окрестности}.
2) Пусть х- любое значение из этой окрестности, но х ¹ а.
Тогда между точками х и а найдется такая точка e, что справедлива формула(формула Тейлора):
![]()
выражение:
![]() называется
остаточным членом в форме Лагранжа.
называется
остаточным членом в форме Лагранжа.
Пусть
функция
![]() имеет
в точке
имеет
в точке
![]() производные всех порядков до n-го
включительно. Тогда для
справедлива
формула Тейлора:
производные всех порядков до n-го
включительно. Тогда для
справедлива
формула Тейлора:
![]()
![]() ,где
,где![]() , называется остаточным членом формулы
Тейлора в форме Пеано;
, называется остаточным членом формулы
Тейлора в форме Пеано;
![]() — бесконечно малая более высокого
порядка малости, чем
— бесконечно малая более высокого
порядка малости, чем![]() .
.
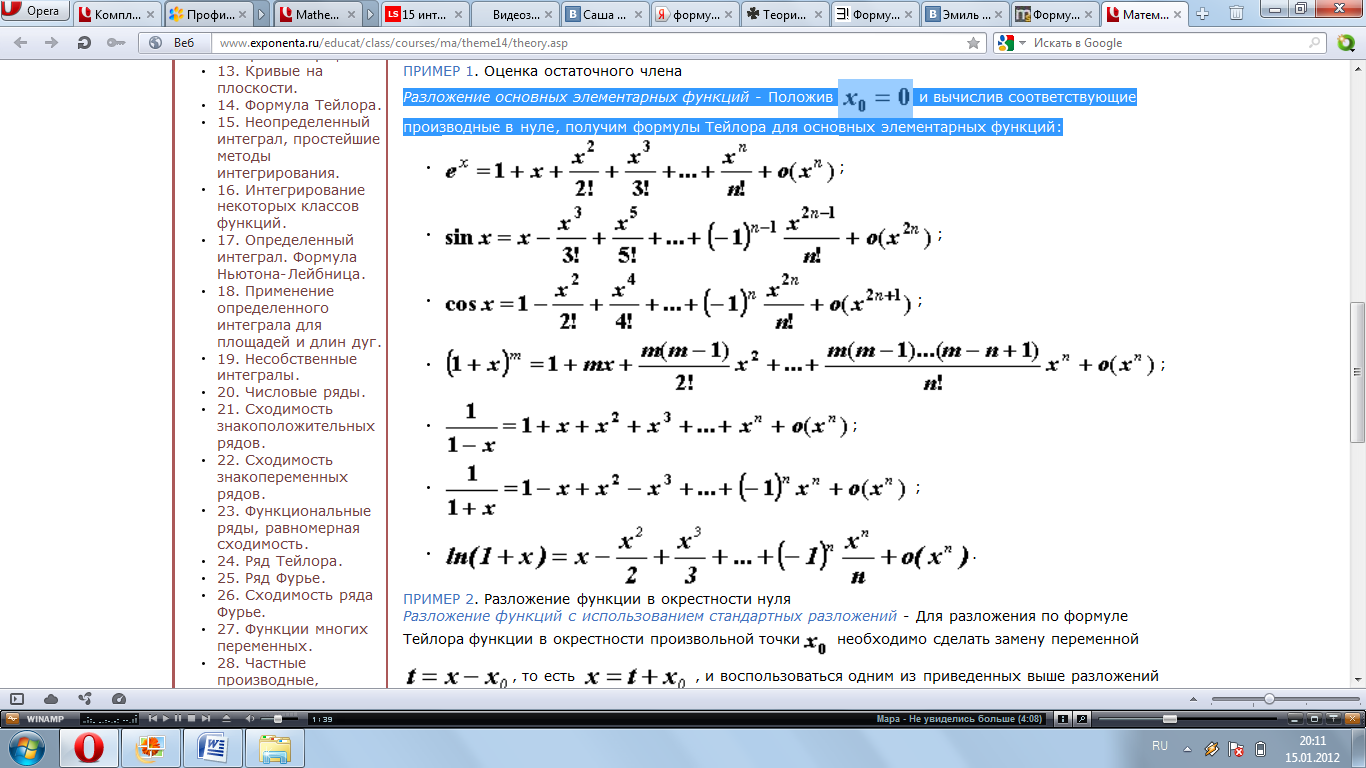
Разложение
основных элементарных функций - Положив![]() и вычислив соответствующие производные
в нуле, получим формулы Тейлора для
основных элементарных функций:
и вычислив соответствующие производные
в нуле, получим формулы Тейлора для
основных элементарных функций:
ВОПРОС№33: основные свойства неопределенного интеграла:
1) Производная неопределенного интеграла равна подынтегральной функции. Дифференциал от неопределенного интеграла равен подынтегральному выражению, т.е. (∫f(x)dx)′=f(x) d∫f(x)dx=f(x)dx
Доказательство:
∫f(x)dx=F(x)+C,
(∫f(x)dx)′=(F(x)+C)′=F′(x)+0=F′(x)=f(x),
d∫f(x)dx=(∫f(x)dx)′dx=f(x)dx
2) Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной, т.е. ∫dF(x)dx=F(x)+C.
Доказательство:
dF(x)=F′(x)dx=f(x)dx,
∫dF(x)dx=∫f(x)dx=F(x)+C.
3) Постоянный множитель можно выносить из под знака интеграла, т.е. ∫kf(x)dx=k∫f(x)dx,k(не равно) 0
Доказательство: Пусть F(x) -- первообразная для функции f(x), тогда
kF(x) -- первообразная для функции kf(x).
(kF(x))′=0+kF′(x)=kF′(x)=kf(x).
Таким образом
∫kf(x)dx=kF(x)+C=k(F(x)+C/k)=k(F(x)+C1)=k∫f(x)dx
4) Неопределенный интеграл от суммы(разности) двух функций равен сумме(разности) интегралов этих функций.
∫[f(x)±g(x)]dx=∫f(x)dx±∫g(x)dx
Распространяется на n слагаемых.
Доказательство:
d[∫f(x)dx±∫g(x)dx]=d∫f(x)dx±d∫g(x)dx=
=f(x)dx±g(x)dx=[f(x)±g(x)]dx.
ВОПРОС№34: Методы интегрирования.
Непосредственное интегрирование.
Пример.Найдите
множество первообразных функции
![]() .
Решение.Запишем
функцию в виде
.
Решение.Запишем
функцию в виде
![]() .
Так
как интеграл суммы функций равен сумме
интегралов, то
.
Так
как интеграл суммы функций равен сумме
интегралов, то
 Числовой
коэффициент можно вынести за знак
интеграла:
Числовой
коэффициент можно вынести за знак
интеграла:
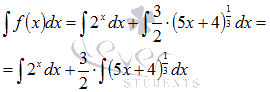 Первый
из интегралов приведен к табличному
виду, поэтому из таблицы первообразных
для показательной функции имеем
Первый
из интегралов приведен к табличному
виду, поэтому из таблицы первообразных
для показательной функции имеем
![]() .
Для
нахождения второго интеграла
.
Для
нахождения второго интеграла
![]() воспользуемся
таблицей первообразных для степенной
функции
воспользуемся
таблицей первообразных для степенной
функции
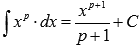 и
правилом
и
правилом
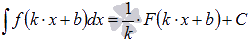 То
есть,
То
есть,
 .
Следовательно,
.
Следовательно,
 где.
где.
Интегрирование по частям.
Интегрирование
по частям основано на представлении
подынтегрального выражения в виде
произведения
![]() и
последующем применении формулы
и
последующем применении формулы
![]() .
Этот метод является очень мощным
инструментом интегрирования. В зависимости
от подынтегральной функции, метод
интегрирования по частям иногда
приходится применять несколько раз
подряд до получения результата. Для
примера найдем множество первообразных
функции арктангенс.
Пример.Вычислить
неопределенный интеграл
.
Этот метод является очень мощным
инструментом интегрирования. В зависимости
от подынтегральной функции, метод
интегрирования по частям иногда
приходится применять несколько раз
подряд до получения результата. Для
примера найдем множество первообразных
функции арктангенс.
Пример.Вычислить
неопределенный интеграл
 .
Решение.Пусть
.
Решение.Пусть
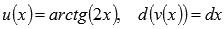 ,
тогда
,
тогда
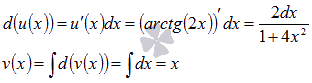 Следует
отметить, что при нахождении функции
v(x)
не прибавляют произвольную постоянную
С.
Теперь
применяем формулу интегрирования по
частям:
Следует
отметить, что при нахождении функции
v(x)
не прибавляют произвольную постоянную
С.
Теперь
применяем формулу интегрирования по
частям:
 Последний
интеграл вычислим по методу подведения
под знак дифференциала.
Так как
Последний
интеграл вычислим по методу подведения
под знак дифференциала.
Так как
![]() ,
то
,
то
![]() .
Поэтому
.
Поэтому
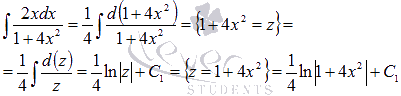 Следовательно,
Следовательно,
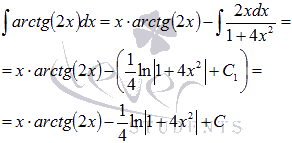 где
где
![]() .
Ответ:
.
Ответ:
![]() .
.
