24.Ортогонализация Грамм-Шмидта

Теорема. В произвольном n-мерном евклидовом пространстве существует ортонормированный базис.

Использованная в доказательстве процедура построения ортонормированного базиса из произвольного базиса :

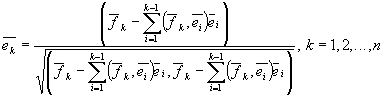
называется процедурой ортогонализации Грамма-Шмидта.

25.Приведение квадратной матрицы к диагональному виду

Матрица А называется подобной матрице В, если найдется такая невырожденная матрица Т, что B=T^-1AT. Характеристи­ческие многочлены подобных матриц совпадают и, значит, подо­бные матрицы имеют одни и те же собственные значения.

Если матрица А подобна диагональной матрице B=T^-1AT, то говорят, что матрица Т приводит матрицу А к диагональному виду. Числа λ₁, λ₂, …, λ_n стоящие на главной диагонали матрицы В, являются собственными значениями матрицы А, а i-й столбец матрицы Т—собственным вектором матрицы А, принадлежа­щим собственному значению λ_i, i=1,2,…,n

Квадратная матрица А порядка n тогда и только тогда приво­дится к диагональному виду, когда у матрицы А имеется n линей­но независимых собственных векторов. Матрица T, столбцами которой служат координаты этих собственных векторов, приво­дит матрицу А к диагональному виду. Этот критерий, в частно­сти, выполняется, когда у матрицы порядка n имеется n различ­ных собственных значений.

Для каждой матрицы А можно построить такую матрицу В, у которой все собственные значения различны, а ее элементы отличаются по абсолютной величине от элементов матрицы А не более чем на ε, где ε — наперед заданное сколь угодно малое положительное число.

Правило построения матрицы Т, приводящей матрицу А порядка n к диагональному виду В.

1)Находят все собственные значения матрицы А.

2)Для каждого собственного значения λ_i ищут фундаменталь­ную систему решений однородной CЛУ

(A - λ_iE)x=0.

3)Строят матрицу Т, столбцами которой являются коор­динаты решений всех найденных фундаментальных систем.

4)Если полученная матрица Т является квадратной, то она приводит матрицу А к диагональному виду. Если же матрица Т не будет квадратной, то матрица А не может быть приведена к диагональному виду.

26.Ортогональные и симметрические матрицы

Для каждой симметрической матрицы существует такая ор­тогональная матрица Q, что

Q^-1AQ— диагональная матрица. Построение этой ортогональной матрицы осуществляется следу­ющим образом:

1.строят невырожденную матрицу Т, которая приводит мат­рицу А к диагональному виду;

2.подвергают столбцы найденной матрицы Т процессу ор­тогонализации, а затем нормируют полученные векторы;

3.строят ортогональную матрицу Q, столбцами которой яв­ляются координаты полученной ортонормированной системы векторов.

27.Понятие квадратичной формы.

Стандартный и канонический вид.

Определение. Квадратичной формой  переменных ,принимающих числовые значения , называется числовая функция вида

  ,где - числа, называемые коэффициентами квадратичной формы.

Определение. Матрицей квадратичной формы  переменных , называется симметрическая матрица порядка , элементы главной диагонали которой совпадают с коэффициентами при квадратах переменных, а каждый недиагональный элемент, расположенный в ой строке ом столбце, равен половине коэфициента при  в квадратичной форме.

Определение. Рангом квадратичной формы называется ранг её матри-цы. Квадратичная форма может быть записана в матричном виде  где матрица квадратичной формы и .

Определение. Квадратичная форма называется канонической (имеет канонический вид), если коэфициенты при , то есть, если матрица квадратичной формы диагональная и следовательно

.,

где не все коэффициенты  равны нулю.

Теорема (Лагранжа). Для всякой квадратичной формы существует такой базис, в котором квадратичная форма имеет канонический вид.

Определение. Нормальным видом квадратичной формы называется такой канонический вид, в котором коэффициенты при квадратах неизвестных (не считая нулевых) равны .

Определение. Квадратичная форма  называется положительно

(отрицательно) определённой, если  при всех

108

 и положительно (отрицательно) полуопределённой,если  при всех .

Теорема (критерий Сильвестра). Для того чтобы квадратичная форма  была положительно определённой, необходимо и достаточно чтобы все угловые миноры матрицы квадратичной формы были положительны,то есть, чтобы

Здесь -угловые миноры матрицы квадратичной формы.

Следствие. Для того чтобы квадратичная форма  была отрицательно определённой, необходимо и достаточно, чтобы знаки угловых миноров матрицы квадратичной формы чередовались следующим образом: