Поверхностные силы

Поверхностные силы – силы, величины которых пропорциональны площади. К ним относят два вида сил. Силы поверхностного натяжения и силы вязкого трения. Последние проявляются только при движении жидкости и не играют никакой роли, когда жидкость находится в покое. Эти силы, как свойство вязкости, были рассмотрены при изучении свойств жидкостей.

Силы поверхностного натяжения

М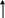 олекулы жидкости притягиваются друг к другу с определённой силой. Причём внутри жидкости силы, действующие на любую молекулу, уравновешиваются, т.к. со всех сторон от неё находятся одинаковые молекулы, расположенные на одинаковом расстоянии. Однако молекулы жидкости, находящиеся на границе (с газом, твердым телом или на границе двух несмешивающихся жидкостей) оказываются в неуравновешенном состоянии т.к. со стороны другого вещества действует притяжение других молекул, расположенных на других расстояниях. Возникает преобладание какой-то силы. Под влиянием этого воздействия поверхность жидкости стремится принять форму, соответствующую наименьшей площади. Если силы внутри жидкости больше наружных сил, то поверхность жидкости стремится к сферической форме. Например, малые массы жидкости в воздухе стремятся к шарообразной форме, образуя капли. Может иметь место и обратное явление, которое наблюдается как явление капиллярности. В трубах малого диаметра (капиллярах) наблюдается искривление свободной поверхности, граничащей с газом или с парами этой же жидкости. Если поверхность трубки смачивается, свободная поверхность жидкости в капилляре вогнутая. Если нет смачивания, свободная поверхность выпуклая, как при каплеобразовании. Во всех этих случаях силы поверхностного натяжения обусловливают дополнительные напряжения p_пов в жидкости. Величина этих напряжений определяется формулой

.

где σ - коэффициент поверхностного натяжения,

r - радиус сферической поверхности, которую принимает жидкость.

Э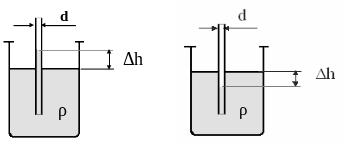 ти дополнительные напряжения легко наблюдать, если в сосуд с жидкостью погрузить капилляр. В этом опыте возможны два варианта. В первом случае жидкость, за счёт поверхностных сил, поднимется по капилляру на некоторую высоту. Тогда говорят о капиллярном поднятии, и наблюдается явление смачивания.

Во втором варианте жидкость опускается в капилляре ниже уровня жидкости в сосуде. Такое явление называют капиллярным опусканием, которое происходит при несмачивании.

В обоих случаях величина пропорциональна дополнительному напряжению, вызванному в жидкости поверхностными силами. Она равна

;

где σ - коэффициент поверхностного натяжения,

d – диаметр капилляра,

k – коэффициент пропорциональности, который выражается следующей формулой

,

и зависит от жидкости. Например, при t = 20 ºC, k спирта составляет 11,5, ртути –10,15 а воды - 30.

Поднятие воды в капиллярах почвы и грунтов является важным фактором в распространении воды. Высота капиллярного поднятия в грунтах изменяется от нуля (галечники) почти до 5 м (глины). При этом с увеличением минерализации воды высота капиллярного поднятия увеличивается.

Поверхностное натяжение и капиллярные эффекты определяют закономерности движения жидкости в условиях невесомости.

К поверхностным силам относятся и силы давления, т.к. они действуют на поверхности жидкости.