Параметры информационной помехи

Огибающая

Увеличим сигнал-шум:

1. Увеличится сигнал – энергетические методы исполнения усилителей;

2. Фильтровый метод – уменьшает полосу пропускания.

Методы борьбы с шумом:

1. Увеличивают отношение «сигнал-шум»: увеличивают сам сигнал – ставят усилители (но увеличивается и шум);

2. Фильтровой метод – уменьшает полосу пропускания (уменьшается скорость передач).

3. Прием по одной из составляющих.

Взаимодействие сигнала с помехой

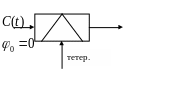
Оценка помехоустойчивости двоичных сигналов

Оценка помехоустойчивости двоичных сигналов – оценивается вероятностью ошибочного приема ( ).

Различают 3 вида помехоустойчивости:

• Статическая – вероятность появления сигнала, когда передатчик молчит;

• Активная помехоустойчивость;

• Пассивная помехоустойчивость.

Статическая помехоустойчивость характеризуется, в основном, в виде сложного сигнала представляемого в кодированном виде. Статическая помехоустойчивость гостирована для всех дискретных систем.

Активная помехоустойчивость – вероятность трансформации единичного сигнала к другой или одного сообщения в другое при его передачи.

Пассивная помехоустойчивость - вероятность обнаружения ошибки при передаче при известных помехах.

Все эти три вида помехоустойчивости должны присутствовать.

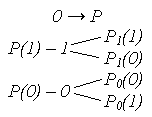
Если канал симметричен P₀(1) = P₁(0)

Канал, у которого P₁(0) + P₁(1)= 1 называют простым.

Вероятность, когда может произойти ошибочный прием, только в случае если есть помеха.

P(σ) -вероятность появления помехи, поэтому вероятность появления ошибочного приема P_ош = P(σ)P₀(0)P₀(1) + P(σ)P₁(1)P₁(0)

P_ош = 0,5P(σ)[P₀(1) +P₁(0)]

Если помеха флуктационная, ошибочный прием: P_ош = 0,5[P₀(1) +P₁(0)], P(σ) = 1.

Для импульсной помехи P(σ) = P₁ = ieⁱ , i = T_б f_сп

где i – интенсивность помехи на базу передаваемого сигнала

Статическая помехоустойчивость для сложного сигнала

0 1 1 1 0 1 0 1 – P⁵_ош – P_стац

P₀(1) = P₁(0) = P_ош (для симметричного канала).

Отсутствие передачи – 0 0 0 0 0 0 0 0. Чем больше единиц, тем выше помехоустойчивость.

Активная помехоустойчивость – вероятность ошибочного приема можно повысить для элементарного сигнала и кодового сообщения за счет повторения передаваемого сигнала (дублирования).

P_1ош = 10^–2

P_ош = P_1ош∙P_2ош =10^–4

Активная помехоустойчивость при передаче кодовых сигналов – применение кодов, исправляющих ошибки.

Пассивная помехоустойчивость – коды, обнаруживающие ошибки.

P_пр = 1 – P_ош – P_пас

P_ош = C^m_n P^m_ош(1 – P_n)^n–m

Оценка элементарного сигнала

S(t) = S_m sinω₀ t, t t_и.

1 – S(t)

0 – 0

Учитывая, что огибающая В имеет закон распределения - закон Релея

P₁(1) = P(C ≥ S₀)

P₁(0) = P(C < S₀)

P₀(0) = P(B < S₀)

P₀(1) = P(B ≥ S₀)

- обобщенный закон Релея

I₀ – коэффициент нулевого порядка Бесселевой функции разложения по аргументу.

P_ош = 0.5[P₁(0)+P₀(1)]

Введем относительные величины:

Если обозначить

Если отыскать минимум этой функции по h, то получим, что при z оптимальном или :

Если h≥3, то

Чем больше h, тем меньше вероятность ошибки.