33.Параболоиды и цилиндрические поверхности.

Параболоиды.

Эллиптический.

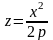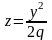При пересечении поверхности координатами плоскостями Oxz и Oyz получается соответственно параболы и . Таким образом, поверхность, определяемая уравнением, имеет вид выпуклой, бесконечно расширяющейся чаши.

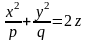
Гиперболический.

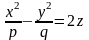
Рассечем поверхность плоскостями z=h. Получим кривую

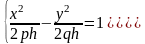
которая при всех h≠0 является гиперболой. При h>0 ее действительные оси параллельны оси Ox, при h<0 – параллельные оси Oy. При h=0 линия пересечения распадается на пару пересекающихся прямых:

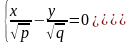
При пересечении поверхности плоскостями, параллельности плоскости Oxz (y=h), будут получаться параболы, ветви которых направлены вверх.

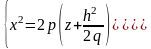
Цилиндр.

Поверхность, образованная движением прямой L, которая перемещается в пространстве, сохраняя постоянное направление и пересекая каждый раз некоторую кривую К, называется цилиндром. При этом кривая К называется направляющей цилиндра, а прямая L – образующая.

- уравнение цилиндра

34.Общее понятия о евклидовой, аффинной и проективной геометриях.

Евклидова геометрия характеризуется такими преобразованиями, при которых:

1. прямая переходит в прямую

2. длины отрезков не меняются

Афинная:

1. прямые переходят в прямые

x=a₁₁x^’+a₁₂y^’

y=a₂₁x^’+a₂₂y^’

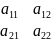≠0

Проективная: Бесконечно удаленная прямая ( )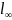

1. Все прямые пересекаются в бесконечно удаленной точке

2. Все линии второго порядка неразличимы

35. Основные понятия неевклидовой геометрии.

Если предположить, что аксиома формулируется определенным образом, то можно получить Евклидову (неевклидову) геометрию.

Если в геометрии Евклида через точки лежащие на прямой провести 1 прямую, не имеющих общих точек с данной, то получим геометрию Евклида.

Если предположить, что таких прямых будет более 1, то получится геометрия Лобачевского.

Если таких прямых не существует – Римана.

36.Многомерное пространство и координаты в нем.

Многомерное пространство, пространство, имеющее число измерений (размерность) более трёх. Обычное евклидово пространство, изучаемое в элементарной геометрии, трёхмерно; плоскости — двумерны, прямые — одномерны. Возникновение понятия  Простейшими Многомерное пространство являются n-мерные евклидовы пространства, где n может быть любым натуральным числом. Подобно тому, как положение точки обычного евклидова пространства определяется заданием трёх её прямоугольных координат, «точка» n-мерного евклидова пространства задаётся n «координатами» x₁, x₂, ..., x_n (которые могут принимать любые действительные значения); расстояние r между двумя точками M(x₁, x₂, ..., x_n) и М"(у₁, y₂, ..., y_n) определяется формулой аналогичной формуле расстояния между двумя точками обычного евклидова пространства. С сохранением такой же аналогии обобщаются на случай n-мерного пространства и другие геометрические понятия. Так, в Многомерное пространство рассматриваются не только двумерные плоскости, но и k-мерные плоскости (k < n), которые, как и в обычном евклидовом пространстве, определяются линейными уравнениями (или системами таких уравнений). Понятие n-мерного евклидова пространства имеет важные применения в теории функций многих переменных, позволяя трактовать функцию n переменных как функцию точки этого пространства и тем самым применять геометрические представления и методы к изучению функций любого числа переменных (а не только одного, двух или трёх). Это и было главным стимулом к оформлению понятия n-мерного евклидова пространства.Вообще n-мерным пространством называется топологическое пространство, которое в каждой своей точке имеет размерность n. В наиболее важных случаях это означает, что каждая точка обладает окрестностью, гомеоморфной открытому шару n-мерного евклидова пространства.