28.Взаимное расположение плоскостей в пространстве.

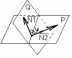
N₁,N₂-нормальные векторы плоскости.

P:A₁x+B₁y+C₁z+D₁=0

Q:A₂x+B₂y+C₂z+D₂=0

P^Q{A₁,B₁,C₁}

Q^N₂{A₂,B₂,C₂}

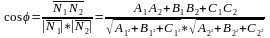
1)Пусть P^Q<=>N₁^N₂

A₁A₂+B₁B₂+C₁C₂=0 условие перпендикулярности P^Q.

2) Пусть P^Q<=> N₁^N₂

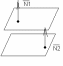
A₁/A₂=B₁/B₂=C₁/C₂- Условие параллельности 2х плоскостей.

A₁/A₂=B₁/B₂=C₁/C₂=D₁/D₂- Условие совпадения 2х плоскостей

29.Нормальное уравнение плоскости.

_{Вектор n0- единичный вектор пл-ти, cosα, cosβ, cosγ; γ,α,β – углы м-ду осями. Вектор n0(cosα, cosβ, cosγ)}

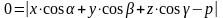
Сумма квадратов косинусов =1.

30.Уравнение пучка плоскостей.

Пучком пл-тей наз-ся мн-во всех пл-тей, проходящ. ч-з линию пересеч-я 2-х данных пл-тей.

A1x+B1y+C1z+D1=0 (1) две не парал. пл-ти.

A2x+B2y+C2z+D2=0 (2)

(3) α(A1x+B1y+C1z+D1)+β(A2x+B2y+C2z+D2)=0 ур-е пучка пл-тей.

Теорема: Ур-е (3) при любых α и β не равных 0, опр-т пл-ть, прохлдящ я-з линю пересеч-я пл-тей (1) и (2) и наборот.

A(x-x0)+B(y-y0)+C(z-z0)=0

31. Канонические уравнения поверхностей второго порядка.

Поверхности второго порядка в пространстве определяются уравнением второй степени.

a₁₁x²+a₂₂y²+a₃₃z²+2a₁₂xy+2a₁₃xz+2a₂₃yz+a₁x+a₂y+a₃z+a₀=0 (1)

Уравнение (1) называется каноническим если a₁₁²+a₂₂²+a₃₃²+a₁₂²+a₁₃²+a₂₃²≠0 и выполняются следующие условия : 1) a_ij=0 если i≠j

2) если a_ii≠0, то a_i=0 3) a₀ =0, +-1

4) только одно из a_i≠0 i=0,1,2,3,4…

32.Эллипсоид, конус и гиперболоиды.

Эллипсоид.

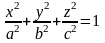
Рассмотрим сечение поверхности с плоскостями, параллельными xOy. Уравнения таких плоскостей z=h, где h – любое число. Линия, получаемая в сечении, определяется двумя уравнениями:

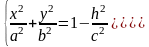
Если |h|>c, c>0, то 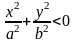точек пересечения поверхности с плоскостями z=h нет.

Если |h|=c, т.е. h=±c, то 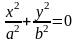. Линия пересечения вырождается в две точки (0;0;с) и (0;0;-с). Плоскости z=c и z=–c касаются поверхности.

Если |h|<c, то уравнения можно переписать в виде:

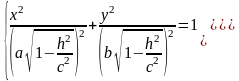
Линия пересечения есть эллипс с полуосями.

Эллипсоид – замкнутая овальная поверхность, где a,b,с – полуоси. Если все они различны, то эллипсоид называется трехосным. Если какие-либо две полуоси равны, то тело называется эллипсоид вращения, если a=b=c, то тело называется сферой x²+y²+z²=R²

Однополостный гиперболоид.

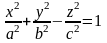
Пересекая поверхность плоскостью z=h, получим линию пересечения, уравнения которой имеют вид.

Полуоси достигают своего наименьшего значения при h=0, a₁=a, b₁=b. При возрастании |h| полуоси будут увеличиваться.

Если пересекать поверхность плоскостями x=h или y=h, то в сечении получим гиперболы. Найдем линию пересечения поверхности с плоскостью Oyx, уравнение которой x=0. Эта линия пересечения описывается уравнениями:

Поверхность имеет форму бесконечно расширяющейся трубки и называется однополостным гиперболоидом.

Двуполостный гиперболоид.

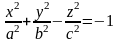
Если поверхность пересечь плоскостями z=h, то линия пересечение уравнениями

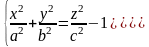
Если |h|<c, то плоскости z=h не пересекаются.

Если |h|=c, то плоскости h=±c касаются данной поверхности соответственно в точках (0;0;с) и (0;0;-с).

Если |h|>c, то уравнения можно переписать в виде:

Эти уравнения определяют эллипс, полуоси которого возрастают с ростом |h|.

У обеих гипербол действительной осью является ось oz. Метод сечения позволяет изобразить поверхность, состоящую из двух полостей, имеющих форму двух неограниченных чаш. Поверхность называется двуполостным гиперболоидом.

Конус.

Поверхность, образованная прямыми линиями, проходящими через данную точку Р и пересекающими данную плоскую линию L (не проходящую через Р) называется конической поверхностью или конусом. При этом линия L называется направляющей конуса, точка Р – ее вершиной, а прямая, описывающая поверхность, называется образующей.

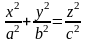- уравнение конуса