8..Смешанное произведение векторов и его свойства.

Смеш-м произведением наз-ся число .

Смысл смешенного произведения: сначала два вектора векторно перемножают, а затем полученный скалярно перемножают с третьим вектором. Смешанное произведение представляет собой число – число. Результат смешанного произведения – объем параллелепипеда, образованного векторами.

Свойства.

1)

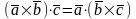
2) Три в-ра компл-ны , если смеш. произв-е =0.

3) а,в,с – правая, если а,в,с>0.

Теорема:

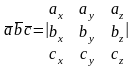
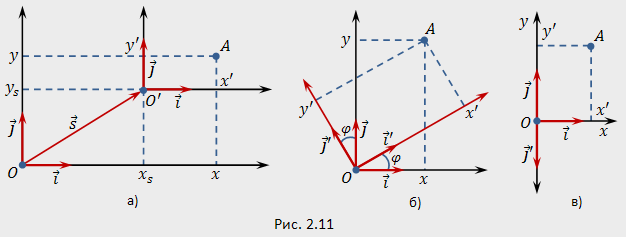
9.Преобразование декартовых прямоугольных координат на плоскости.

Получим формулы, связывающие координаты точки при переходе от одной прямоугольной системы координат к другой прямоугольной системе координат. Рассмотрим три типа преобразований:а) параллельный перенос;б) поворот;

В каждом случае координаты точки в старой и новой системах координат связаны формулой (2.8). Поэтому достаточно найти вектор переноса начала координат и матрицу перехода от базиса к базису .

а) При параллельном переносе системы координат базис не изменяется, поэтому матрица перехода является единичной: . Находим координаты вектора переноса начала координат: . Тогда формулу (2.8) можно записать в виде

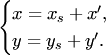б) При повороте системы координат на угол начало новой системы координат совпадает с началом старой, поэтому вектор переноса нулевой: . Разлагая новые базисные векторы по старому базису, получаем , . Составим матрицу перехода, записывая координаты векторов по столбцам: . Тогда формулу (2.8) можно записать в виде

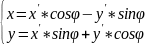
10.Линии на плоскости и их уравнения в координатах. Параметрические уравнения линии.

Уравнением линии l на пл-ти будем называть ур-е F(x;y)=0 (1), если коорд-ты точек линии l удовлетв-т ур-ю(1), а коордю точек линии l, не лежат на линии l неудовл. ур-ю(1)

+ =

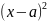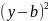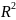
Парам-е ур-е линии: Ур-е вида 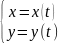, t (a;b) наз-ся параметрическим ур-ем линии l, x,y t,

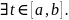
11.Полярные координаты.

Полярная система координат на плоскости — это совокупность точки , называемой полюсом, и полупрямой , называемой полярной осью. Кроме того, задается масштабный отрезок для измерения расстояний от точек плоскости до полюса. Как правило, на полярной оси выбирается вектор , приложенный к точке , длина которого принимается за величину масштабного отрезка, а направление вектора задает положительное направление на полярной оси

П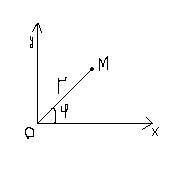 оложение точки в полярной системе координат определяется расстоянием (полярным радиусом) от точки до полюса (т.е. )и углом (полярным углом) между полярной осью и вектором . Полярный радиус и полярный угол составляют полярные координаты точки , что записывается в виде . Полярный угол измеряется в радианах и отсчитывается от полярной оси:

- в положительном направлении (против направления движения часовой стрелки), если значение угла положительное;

- в отрицательном направлении (по направлению движения часовой стрелки), если значение угла отрицательное.

Полярный радиус определен для любой точки плоскости и принимает неотрицательные значения . Полярный угол определен для любой точки плоскости, за исключением полюса , и принимает значения , называемыми главными значениями полярного угла. В некоторых случаях целесообразно считать, что полярный угол определен с точностью до слагаемых , где . В этом

случае значениям полярного угла для всех соответствует одно и то же направление радиус-вектора.

С полярной системой координат можно связать прямоугольную систему координат , начало которой совпадает с полюсом, а ось абсцисс (точнее положительная полуось абсцисс) — с полярной осью. Ось ординат достраивается перпендикулярно оси абсцисс так, чтобы получилась правая прямоугольная система координат Длины базисных векторов определяются масштабным отрезком на полярной оси.

Наоборот, если на плоскости задана правая прямоугольная система координат, то, приняв положительную полуось абсцисс за полярную ось, получим полярную систему координат {связанную с данной прямоугольной).

Выведем формулы, связывающие между собой прямоугольные координаты точки , отличной от точки , и ее полярные координаты . Получаем

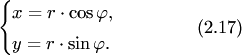
Эти формулы позволяют найти прямоугольные координаты по известным полярным координатам.