
- •1.Направленный отрезок и вектор. Длина отрезка, деление отрезка в данном отношении.
- •2.Векторы и линейные операции над ними.
- •3.Проекция вектора на ось.
- •4.Базис. Координаты вектора.
- •5..Аффинные координаты. Декартовы прямоугольные координаты.
- •6..Скалярное произведение векторов и его свойства.
- •7.. Векторное произведение векторов и его свойства.
- •8..Смешанное произведение векторов и его свойства.
- •9.Преобразование декартовых прямоугольных координат на плоскости.
- •10.Линии на плоскости и их уравнения в координатах. Параметрические уравнения линии.
- •11.Полярные координаты.
- •12.Общее уравнение прямой на плоскости, геометрический смысл его коэффициентов.
- •13.Уравнение прямой с угловым коэффициентом. Уравнение прямой в отрезках.
- •15.Взаимное расположение пары прямых на плоскости и угол между ними.
- •16.Расстояние от точки до прямой.
- •17. Уравнение пучка прямых
- •18.Канонические уравнения линий второго порядка.
- •1 9.Каноническое уравнение эллипса (с выводом уравнения).
- •20.Канонические уравнения гипербола и параболы.
- •21. Эксцентриситет и директрисы линий второго порядка.
- •23. Приведение уравнения второго порядка к каноническому виду.
- •24.Уравнения прямой в пространстве.
- •25.Различные виды уравнений плоскости.
- •26.Взаимное расположение прямой и плоскости в пространстве.
- •27.Взаимное расположение прямых в пространстве.
- •28.Взаимное расположение плоскостей в пространстве.
- •29.Нормальное уравнение плоскости.
- •30.Уравнение пучка плоскостей.
- •32.Эллипсоид, конус и гиперболоиды.
- •33.Параболоиды и цилиндрические поверхности.
- •34.Общее понятия о евклидовой, аффинной и проективной геометриях.
- •35. Основные понятия неевклидовой геометрии.
- •36.Многомерное пространство и координаты в нем.
- •37.Подпространства и выпуклые множества в многомерном пространстве. Выпуклые многогранники.
- •38.Подпространство, заданное системой линейных уравнений. Выпуклые подмножества и системы линейных неравенств.
- •39. Матрицы, виды матриц. Линейные операции над матрицами, их свойства. Умножение матриц, его свойства. Транспонирование матриц.
- •40.Определители матриц 1 и 2 порядков. Миноры и алгебраические дополнения элементов квадратных матриц. Вычисления определителя разложением по элементам строки или столбца.
- •41.Свойства определителей.
- •42. Вычисление определителей с применением свойств определителей.
- •44.Нахождение обратной матрицы методом «прямоугольника».
- •45. Элементарные преобразования матриц.
- •46.Ранг матрицы.
- •47.Метод обратной матрицы для решения слу. Метод обратной матрицы
- •49.Правило Крамера.
- •50. Метод Гаусса, прямой и обратный ход.
- •51. Теорема Кронекера-Капелли
- •52. Системы однородных линейных уравнений, фундаментальная система решений.
- •53. Неоднородные системы линейных уравнений. Структура их решений.
- •54. Системы линейных неравенств и геометрическое представление их решений.
- •56.Модуль и аргумент. Геометрическая интерпретация. Формула Муавра.
- •57. Извлечение корней комплексного числа. Корни из единицы.
- •58. Понятие многочлена и операции над ним.
- •59. Корни многочлена. Основная теорема алгебры Разложение многочлена на простые множители.
- •60. Многочлены с действительными коэффициентами.
25.Различные виды уравнений плоскости.
Уравнение плоскости, проходящей через заданную точку, перпендикулярно данному вектору.
Пусть
плоскость задана точкой M0(x0;y0;z0)
и вектором
 ,
перпендикулярной этой плоскости.
,
перпендикулярной этой плоскости.
Возьмем
произвольную точку M(x;y;z)
и составим вектор
 .
При любом расположении точки М на
плоскости Q
.
При любом расположении точки М на
плоскости Q
 ,
поэтому
,
поэтому
 .
.

Уравнение плоскости, проходящей через три точки
К (х1;у1) М (х2;у2) N (x3;y3)
Возьмем на плоскости точку P (x;y;z).
Составим векторы:

Эти векторы лежат в одной плоскости, следовательно они компланарны:

Параметрические уравнения прямой.



Канонические уравнения прямой.
S(m;n;p)
– направляющий вектор прямой L.
M0(x0;y0;z0)
– точка на прямой.
 соединяет
M0
с произвольной
точкой М.
соединяет
M0
с произвольной
точкой М.

Уравнение прямой в пространстве, проходящей через две точки.
M1(x1;y1;z1) M2(x2;y2;z2)
В
качестве направляющего вектора можно
задать вектор

Следовательно:
 ,
тогда
,
тогда

Общее уравнение прямой.
Уравнение прямой как линию пересечения двух плоскостей. Рассмотрим:



Т.к. прямая перпендикулярна векторам n1 и n2 то направляющий вектор запишется как векторное произведение:

Угол между прямыми.
 ;
;


26.Взаимное расположение прямой и плоскости в пространстве.
Прямая может лежать на данной плоскости, быть параллельна данной плоскости или пересекать ее в одной точке, см. следующие рисунки.

рис.6.

рис.7.

рис.8.
Теорема.
Пусть плоскость
![]() задана
общим уравнением
задана
общим уравнением
![]() ,а
прямая L задана каноническими уравнениям
,а
прямая L задана каноническими уравнениям
 или
параметрическими уравнениями
или
параметрическими уравнениями
 ,
,
![]() ,
в которых
,
в которых
![]() –
координаты
нормального вектора
плоскости
,
–
координаты
нормального вектора
плоскости
,
![]() –
координаты
произвольной фиксированной точки
прямой L,
–
координаты
произвольной фиксированной точки
прямой L, ![]() –
координаты направляющего вектора
прямой L. Тогда: 1) если
–
координаты направляющего вектора
прямой L. Тогда: 1) если
![]() ,
то прямая L пересекает плоскость
в
точке, координаты
которой
,
то прямая L пересекает плоскость
в
точке, координаты
которой
![]() можно
найти из системы
уравнений
можно
найти из системы
уравнений
 ;
(7)
;
(7)
2)
если
![]() и
и
![]() ,
то прямая лежит на плоскости;
,
то прямая лежит на плоскости;
3)
если
и
![]() ,
то прямая параллельна плоскости.
,
то прямая параллельна плоскости.
27.Взаимное расположение прямых в пространстве.
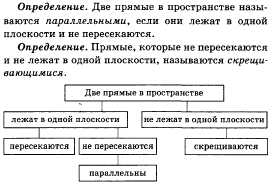
Возможны четыре различных случая расположения двух прямых в пространстве:
– прямые скрещивающиеся, т.е. не лежат в одной плоскости;
– прямые пересекаются, т.е. лежат в одной плоскости и имеют одну общую точку;
– прямые параллельные, т.е. лежат в одной плоскости и не пересекаются;
– прямые совпадают.
точки.
Перечисленным
выше случаям взаимного расположения
прямых
![]() и
и
![]() соответствуют следующие признаки:
соответствуют следующие признаки:
– прямые
и
скрещивающиеся
![]() векторы
векторы
![]() не компланарны;
не компланарны;
– прямые
и
пересекаются
векторы
компланарны,
а векторы
![]() не коллинеарны;
не коллинеарны;
– прямые
и
параллельные
векторы
коллинеарны,
а векторы
![]() не коллинеарны;
не коллинеарны;
– прямые и совпадают векторы коллинеарны.
