21. Эксцентриситет и директрисы линий второго порядка.

Директриссой эллипса (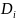 ) соотв. фокусу наз-ся прямая, перепендикулярная большей оси эллипса, расположенной в одной полуплоскости с фокусом и на расстоянии .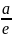

Теорема. Отношение расст-я от любой т. эл-са до соотв. D – есть вел-на постоянная 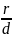=e. =e.

Директриссой гиперболы соотв. фокусу наз-ся прямая, перепендикулярная прямой, соел. фокусы гип-лы и на расст. от центра гип-лы.

Теорема. Отношение расстояния от любой т. гип-лы до фокуса к расстоянию от этой т. до соотв. D – есть вел-на постоянная=e.

Величина e=c/a – называется эксцентриситет, c=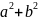

22.Уравнения линий второго порядка в полярных координатах.

Рассмотрим эллипс или параболоид. Выберем реш-я полярную сис-му коорд.так , чтобы ее полюс совпал с левым фокусом, а пол-ю ось направим вдоль большей полуоси эл-са или оси симметрии параболы.

Проведем дирректриссу, QF=p. Возьмем M(r,φ), =e, FM=r

pM=PR+RM=QF=RM=p+r*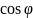

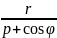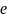= , r=p+e*r*cos ,

r=

r=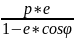 — 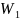правая

→ гипербола.

r=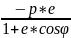 — 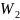левая

23. Приведение уравнения второго порядка к каноническому виду.

Алгоритм. Проверяем, явл-ся линия центральной: решим систему уравнений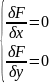 , где F – левая часть ур-я (1). Если сис-ма имеет единств. реш-е, то линия –центральная. Парал-м переносом приведем ур-е линии к виду: A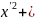 2Bx’y’+ 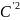+F’=0 (1)

Если линия не центр-я, то следует п.2.Поворотом сис-мы коорд. делаем В’=0. Если линия не центр., выполняем параллельный перенос.

24.Уравнения прямой в пространстве.

Вектор n(А,В,С) – норм. вектор пл-ти, если он препендикулярен этой плоск-ти.

Если задана M₀(x₀;y₀;z₀) на пл-ти, то задание норм. в-ра и точки, ч-з кот-е проходит пл-ть, пл-ть опред-ся однозначно. Возьмем на прямой L точку M(x;y;z).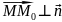 . 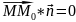— ур-е пл-ти. Обозначим радиус-векторы точек M и M₀ через r и r₀.

_{Вект. ур-е пл-ти:}

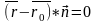
Т.к 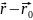=(x-x0;y-y0;z-z0), то в коорд. ф-ме получим ур-е:

A(x-x0)+B(y-y0)+C(z-z0)=0.

Ax+By+Cz+d=0 (1)- общее уравнение пл-ти.

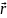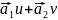= + —векторно-парметрическое ур-е пл-ти.

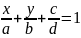— ур-е в отрезках.