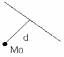
16.Расстояние от точки до прямой.

1. Ax+By+C=0, M₀(x₀,y₀)

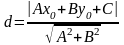
2. Пусть плоскость задана ур-ем Ax+By+Cz+D=0

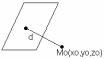
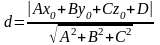
17. Уравнение пучка прямых

Пучком прямых с центром в точке S называют мн-во всех прямых. проходящих ч-з эту точку.

Есть прямые, кот-е не парал-ны и не совп.

α(A1x+B1y+C1) + β(A2x+B2y+C2) = 0.(3)

Теорема: Ур-е (3) опр-т некоторую прямую пучка прямых с центром в точке S при конкретных знач-ях α и β; и наоборот, всякая прямая, проходящ ч-з точку S , задается ур-и (3) при некот-х зн-ях α и β.

18.Канонические уравнения линий второго порядка.

Ур-м 2-го порядка наз-ся ур-е вида A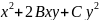 + Dx + Ey + F=0 (1), где

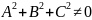
Линией 2-го порядка наз-ся мн-во точек на пл-ти, кот-е удовл-т ур-ю(1) и только ему, т.е. точки не пренадлежащие и не удовлетворяющие ур-ю (1).

Каноническим ур-м линии 2-го порядка наз. ур-е (1), коэффициенты которого удовлетворяют следующим условиям: 1) B=0; 2) A≠0, D=0,C≠0,E=0; 3)F=0,+-1,

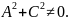
Две пересекающиеся прямые – линни второго порядка.

1 9.Каноническое уравнение эллипса (с выводом уравнения).

Эллипсом называется

геометрическое место всех

точек плоскости, сумма

расстояний от которых до

до фокусов есть величина

постоянная, большая, чем расстояние между фокусами.

Фокусами эл-са явл. точки F₁ (-c;0) и F₂ (c;0), где с=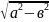

Полуосями наз-ся числа а и в. Если a>b, то а-большая п\ось, а в-меньшая п\ось

Пусть М (х;у) – произвольная точка эллипса.

Т.к. MF₁ + MF₂ = 2a

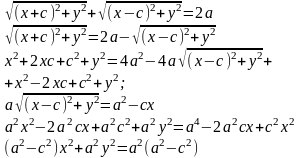
Т.к.

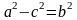
То получаем

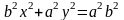
Или

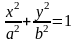
Фокальным радиусом точки М эл-са наз-ся расст-е от т.М до фокусов. 2 равных фок-х радиуса: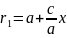 и 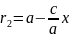. Величина e=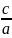 – эксцентреситет эл-са. Центр эл-са-точка, леж-я на сер-не отр-ка F₂F₁

20.Канонические уравнения гипербола и параболы.

Парабола – множество всех точек плоскости, каждая из которых одинаково удалена от фокуса, и директрисы. Расстояние между фокусом и директрисой называется параметром параболы и обозначается через р>0. т. F(p/2;0) – фокус параболы, прямая x =-p/2 –директрисса параболы

Пусть M(x;y) – произвольная

т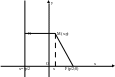 очка M с F. Проведем отрезок

MN перпендикулярно

директрисе. Согласно

определению MF=MN.

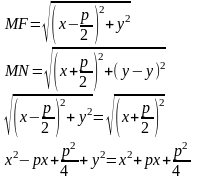
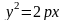
Гиперболой называется множество всех точек плоскости, модуль разности расстояний от каждой из которых до фокусов есть величина постоянная.Числа а и в – действ. и мнимые полуоси.

Пусть M(x;y) – произвольная точка гиперболы. Тогда согласно определению гиперболы |MF₁ – MF₂|=2a или MF₁ – MF₂=±2a,

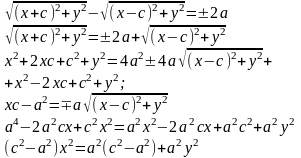
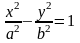
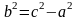
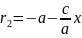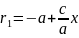A(a,0) и B(-a,0) – Вершины гип-лы. Действ. ось-расст-е от центра гип-лы до вершины. Фокальный радиус: правая ветвь и , левая и