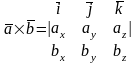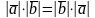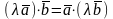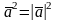- •1.Направленный отрезок и вектор. Длина отрезка, деление отрезка в данном отношении.
- •2.Векторы и линейные операции над ними.
- •3.Проекция вектора на ось.
- •4.Базис. Координаты вектора.
- •5..Аффинные координаты. Декартовы прямоугольные координаты.
- •6..Скалярное произведение векторов и его свойства.
- •7.. Векторное произведение векторов и его свойства.
- •8..Смешанное произведение векторов и его свойства.
- •9.Преобразование декартовых прямоугольных координат на плоскости.
- •10.Линии на плоскости и их уравнения в координатах. Параметрические уравнения линии.
- •11.Полярные координаты.
- •12.Общее уравнение прямой на плоскости, геометрический смысл его коэффициентов.
- •13.Уравнение прямой с угловым коэффициентом. Уравнение прямой в отрезках.
- •15.Взаимное расположение пары прямых на плоскости и угол между ними.
- •16.Расстояние от точки до прямой.
- •17. Уравнение пучка прямых
- •18.Канонические уравнения линий второго порядка.
- •1 9.Каноническое уравнение эллипса (с выводом уравнения).
- •20.Канонические уравнения гипербола и параболы.
- •21. Эксцентриситет и директрисы линий второго порядка.
- •23. Приведение уравнения второго порядка к каноническому виду.
- •24.Уравнения прямой в пространстве.
- •25.Различные виды уравнений плоскости.
- •26.Взаимное расположение прямой и плоскости в пространстве.
- •27.Взаимное расположение прямых в пространстве.
- •28.Взаимное расположение плоскостей в пространстве.
- •29.Нормальное уравнение плоскости.
- •30.Уравнение пучка плоскостей.
- •32.Эллипсоид, конус и гиперболоиды.
- •33.Параболоиды и цилиндрические поверхности.
- •34.Общее понятия о евклидовой, аффинной и проективной геометриях.
- •35. Основные понятия неевклидовой геометрии.
- •36.Многомерное пространство и координаты в нем.
- •37.Подпространства и выпуклые множества в многомерном пространстве. Выпуклые многогранники.
- •38.Подпространство, заданное системой линейных уравнений. Выпуклые подмножества и системы линейных неравенств.
- •39. Матрицы, виды матриц. Линейные операции над матрицами, их свойства. Умножение матриц, его свойства. Транспонирование матриц.
- •40.Определители матриц 1 и 2 порядков. Миноры и алгебраические дополнения элементов квадратных матриц. Вычисления определителя разложением по элементам строки или столбца.
- •41.Свойства определителей.
- •42. Вычисление определителей с применением свойств определителей.
- •44.Нахождение обратной матрицы методом «прямоугольника».
- •45. Элементарные преобразования матриц.
- •46.Ранг матрицы.
- •47.Метод обратной матрицы для решения слу. Метод обратной матрицы
- •49.Правило Крамера.
- •50. Метод Гаусса, прямой и обратный ход.
- •51. Теорема Кронекера-Капелли
- •52. Системы однородных линейных уравнений, фундаментальная система решений.
- •53. Неоднородные системы линейных уравнений. Структура их решений.
- •54. Системы линейных неравенств и геометрическое представление их решений.
- •56.Модуль и аргумент. Геометрическая интерпретация. Формула Муавра.
- •57. Извлечение корней комплексного числа. Корни из единицы.
- •58. Понятие многочлена и операции над ним.
- •59. Корни многочлена. Основная теорема алгебры Разложение многочлена на простые множители.
- •60. Многочлены с действительными коэффициентами.
5..Аффинные координаты. Декартовы прямоугольные координаты.
Пусть
в пространстве фиксирована точка
![]() .
Совокупность точки
и
базиса называется аффинной
(декартовой) системой координат:
.
Совокупность точки
и
базиса называется аффинной
(декартовой) системой координат:
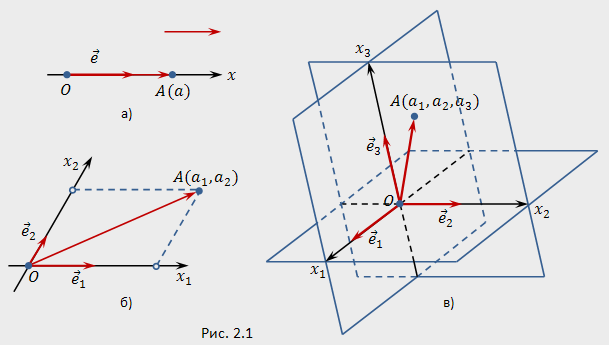
– аффинная
система координат на прямой - это точка
и
ненулевой вектор
![]() на
прямой (базис на прямой);
на
прямой (базис на прямой);
– аффинная
система координат на плоскости - это
точка
и
два неколпинеарных вектора
![]() ,
взятые в определенном порядке (базис
на плоскости);
,
взятые в определенном порядке (базис
на плоскости);
– аффинная
система координат в пространстве - это
точка
и
три некомпланарных вектора
![]() ,
взятые в определенном порядке (базис
в пространстве).
,
взятые в определенном порядке (базис
в пространстве).
Точка
называется началом
координат.
Прямые, проходящие через начало координат
в направлении базисных векторов,
называются координатными
осями:
![]() —
ось абсцисс,
—
ось абсцисс,
![]() —
ось ординат,
—
ось ординат,
![]() —
ось аппликат.
Плоскости, проходящие через две
координатные оси, называются координатными
плоскостями.
—
ось аппликат.
Плоскости, проходящие через две
координатные оси, называются координатными
плоскостями.
Аффинная система координат в пространстве (или на плоскости) называется правой, если ее базис является правым, и левой, если её базис — левый.
Аффинная
система координат называется
прямоугольной,
если ее базис ортонормированный. Выбирая
стандартные базисы получаем:![]() —
прямоугольную
систему координат на прямой
— это точка
и
единичный вектор
—
прямоугольную
систему координат на прямой
— это точка
и
единичный вектор
![]() на
прямой. Точки
и
на
прямой. Точки
и
![]() на координатной оси
на координатной оси
![]() обозначаются
обозначаются
![]() и
и
![]() ;
;
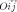
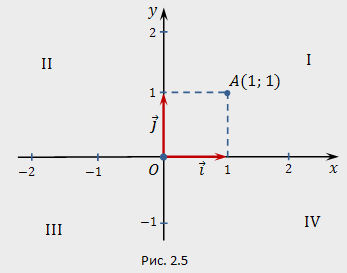
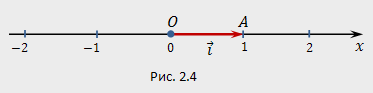 —
прямоугольную
систему координат на плоскости
— это точка
и
два взаимно перпендикулярных единичных
вектора
и
—
прямоугольную
систему координат на плоскости
— это точка
и
два взаимно перпендикулярных единичных
вектора
и
![]() на
плоскости (вектор
—
первый базисный вектор, a
—
второй; пара векторов
на
плоскости (вектор
—
первый базисный вектор, a
—
второй; пара векторов
![]() —
правая). Координатные оси
(абсцисс)
и
—
правая). Координатные оси
(абсцисс)
и
![]() (ординат)
разбивают плоскость на 4 части, называемые
квадрантами
(четвертями).
Точка
(ординат)
разбивают плоскость на 4 части, называемые
квадрантами
(четвертями).
Точка
![]() ,
например, принадлежит
,
например, принадлежит
![]() четверти;
четверти;
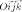 —
прямоугольную
систему координат в пространстве
— это точка
и
три попарно перпендикулярных единичных
вектора
—
прямоугольную
систему координат в пространстве
— это точка
и
три попарно перпендикулярных единичных
вектора
![]() (вектор
—
первый базисный вектор,
—
второй, а
(вектор
—
первый базисный вектор,
—
второй, а
![]() —
третий; тройка векторов
—
правая). Координатные оси обозначаются:
—
ось абсцисс,
—
ось ординат,
—
третий; тройка векторов
—
правая). Координатные оси обозначаются:
—
ось абсцисс,
—
ось ординат,
![]() —
ось аппликат. Координатные плоскости
—
ось аппликат. Координатные плоскости
![]() ,
проходящие через пары координатных
осей, разбивают пространство на 8
октантов.
Точка
,
проходящие через пары координатных
осей, разбивают пространство на 8
октантов.
Точка
![]() ,
например, принадлежит
октанту.Прямоугольные
системы координат обозначают также
указанием начала координат и координатных
осей, например,
,
например, принадлежит
октанту.Прямоугольные
системы координат обозначают также
указанием начала координат и координатных
осей, например,
![]() .
.
6..Скалярное произведение векторов и его свойства.
Скалярным произведением двух ненулевых векторов называется число, равное произведению этих векторов на косинус угла между ними.
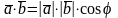
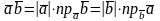
Cв-ва:
3.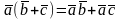
Векторы а и в наз-ся ортогональными, если угол м-ду ними равен 90 градусов.
Теорема: Два ненулевых вектора ортогональны, если их СПВ =0.
а*в=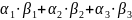
cosφ=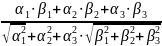
7.. Векторное произведение векторов и его свойства.
Тройка векторов а,в,с наз. правоориентированной (правой), если с конца 3го вектора с кратчайший поворот от 1го ко 2му вектору мы будем видеть против час. стрелки. Если кратчайший поворот от 1го ко 2му по час. стрелки - левая. Векторным произведением 2х векторов а и в наз. такой вектор с, который удовлетворяет условиям: 1) |c|=|a|*|b|*sinj. 2) c^a и c^b. 3) тройка а,в,с-правая.
Св-ва: 1)Вект. произв-е численно равно площади параллепипеда, постр. на этих вект-х.2)а*в=-в*а.3) (α*а)*в=α*(а*в).
Теорема: Два в-ра коллинеарны тогда, когда их вект. произв-е =0.
Теорема: