51. Теорема Кронекера-Капелли

Рассмотрим систему m-линейных уравнений с n-неизвестными.

a₁₁x₁+a₁₂x₂+…+a_1nx_n=b₁

a₂₁x₁+a₂₂x₂+…+a_2nx_n=b₂

a_m1x₁+a_m2x₂+…+a_mnx_n=b_m

A=

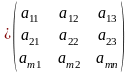
Расширенной матрицей назовем

А (с волной) = a₁₁ a₁₂ … a_1nb₁

a₂₁ a₂₂ … a_2nb₂

a_m1 a_m2 … a_mn b_m

b₁ x₁

B=b₂ X=x₂

b_n x_n

Тогда система будет иметь сл. вид: AX=B

Система называется совместной, если она имеет хотя бы одно решение. Если не имеет решений – несовместной.

Теорема Кронекера-Капелли: Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы, причём система имеет единственное решение, если ранг равен числу неизвестных, и бесконечное множество решений, если ранг меньше числа неизвестных.

Лемма (о базисном миноре): базисные строки (столбцы) матрицы линейно-независимы. Остальные строки (столбцы) выражаются в виде линейных комбинаций базисных

52. Системы однородных линейных уравнений, фундаментальная система решений.

Рассмотрим систему линейных уравнений Ах=0 (1). Такая система называется однородной. Однородная система всегда имеет решение. Такое решение называется тривиальным.

Пусть ранг матрицы А равен r:

1. r=n, n-число неизвестных

m=n – матрица квадратная

m>n – можем выделить базисный минор, который можно разместить в верхней части матрицы и с Леммы о базисном миноре следует, что остальные строки А выражаются в виде линейный комбинаций базисных строк, поэтому последнее m-n-уравнение можно отбросить

2. r<n

Пусть базисный минор А, располагается в верхнем углу. Неизвестные коэффициенты которых образованы базисным минором называются базисными, остальные –свободными.

(свободные члены переносим в правую часть, базисные – в левую)

3. Если ранг меньше числа неизвестных, то однородная система имеет неправильное решение.

Свойства решений однородно системы: 1) если x₁, x₂ решение однородной системы (1), то и х= x₁+ x₂ также решение этой системы.

2)если x₁ решение системы (1), что Х=с* x₁ также решение системы.

3) существует n-r линейно-независимых решений системы (1). Эти решения образуют фундаментальную систему решений однородной системы уравнений.

4) такое решение х системы (1) может быть представлено в виде

Х=с₁Х⁽¹⁾+…+с_n-rX^n-r, где Х⁽¹⁾ ….X^n-r – фундаментальная система решений.

53. Неоднородные системы линейных уравнений. Структура их решений.

Рассмотрим неоднородную линейную систему уравнений. Ax=b b≠0

Такая система называется неоднородной. Столбец b называется неоднородностью системы линейных уравнений (СЛУ)

Будем рассматривать соответствующую систему (1) однородную систему Ax=0

Свойства решений неоднородных СЛУ: 1) разность двух решений системы (1) явл. решением системы (2) 2)сумма некоторого решения системы (1) и системы (2) является решением системы (1) 3) всякое решение неоднородной системы (1) можно представить в виде суммы некоторого фиксированного решения (1) и некоторого решения неоднородной системы (2).

Для того чтобы построить общее решение, т.е. решение, которое содержит все решения неоднородной системы, надо найти некоторое решение однородной системы, которое называется частным решением, а затем найти общее решение соответствующей однородной системы. Сумма этих решений содержит все решения неоднородной системы, а поэтому явл. общим решением.