47.Метод обратной матрицы для решения слу. Метод обратной матрицы

Если det A ≠ 0, то существует обратная матрица . Тогда решение СЛАУ записывается в виде: . Следовательно, решение СЛАУ свелось к умножению известной обратной матрицы на вектор правых частей. Таким образом, задача решения СЛАУ и задача нахождения обратной матрицы связаны между собой, поэтому часто решение СЛАУ называют задачей обращения матрицы. Проблемы использования этого метода те же, что и при использовании метода Крамера: нахождение обратной матрицы – трудоемкая операция.

48.Модель Леонтьева межотраслевого баланса.

Состоит в следующем. Пусть имеется n предприятий, каждое из которых выпускает однородный вид продукции. Пусть Q1 ,Q2…Qn валовый выпуск каждого вида продукции. Каждое предприятие для выпуска своей продукции использует некоторое количество продукции, произведенной другими предприятиями. Обозначим 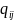- количество продукции i-вида, потребляемое j- пердприятием.

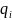– конечный продукт i-предприятия.

Можно составить n неравенств, которые называются балансовыми уравнениями:

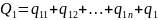
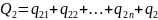
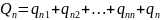
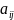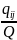= - - величина, показывающая какое количество i-вида продукции необходимо для выпуска единицы j-вида продукции.

Числа называются коэффициентами прямых затрат Матрица А 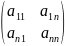называется матрицей коэффициентов прямых затрат.

Поскольку = * 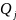(2), то систему (1) можно представить в виде:

Подставим выражение (2) в систему неравенств (1) и получим :

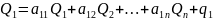
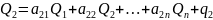(3)

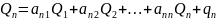
Тогда систему (3) можно переписать в таком виде:

Q = A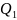 + G

EQ=AQ+G

(E-A)Q=G

Q=(E-A)^-1G

B= (E-A)^-1 – матрица полных затрат

G=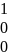 Q=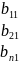

Элементы 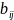показывают какое количество продукции i-вида надо произвести, чтобы получить единицу продукта конечного вида.

49.Правило Крамера.

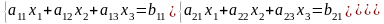
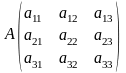
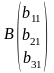
Подсчитать определитель матрицы А.

Затем матрицей B заменить первый столбец матрицы А, подсчитать определитель и разделить его на detA, так мы получим x₁. То же самое проделать со 2-ым и 3-им столбцом.

50. Метод Гаусса, прямой и обратный ход.

Метод Гаусса состоит в приведении матрицы системы одновременно и расширенной матрицы к трапециевидному или ступенчатому виду, применяя для этого элементарные преобразования к строкам матрицы.

После таких преобразований равносильная исходная системе СЛУ будет иметь следующий вид:

a₁₁x₁+a₁₂x₂+…+a_1nx_n=b₁

a_2kx₂+…+a_2nx_n=b₂

a_3px₃+…+a_3nx_n=b₃

…………………………

a_eix_i+…+a_enx_n=b_c

0=b_e+1

…………………………

a₁₁x₁+a_1kx_k+…+a_1ix_i=b₁+…a₁₂x₂

a_2kx_k+…+a_2ix_i=b₂+…

…………………………….

a_eix_i=b_i Придавая свободным переменным (в правой части) произвольные значения мы последовательно найдем все решения этой системы.