1.Направленный отрезок и вектор. Длина отрезка, деление отрезка в данном отношении.

Отрезок, у которого указаны начало и коней наз-ся направленным. Направленный вектор явл-ся связанным. Свободные в-ры характ-ся длиной и направлением.

2 вектора наз. коллинеарными, если они лежат на 1 прямой или ||-ных прямых. Векторы наз. компланарными, если они лежат в 1-ой плоскости или в ||-ных плоскостях. 2 вектора равны, когда они коллинеарны, сонаправленны, и имеют одинак-ую длинну.

2.Векторы и линейные операции над ними.

1 )Умножение на число: произведение вектора А на число l наз. такой вектор В, который обладает след. св-ми: а) А||В. б) l>0, то А­­В, l<0, то А­¯В. в)l>1, то А<В, )l<1, то А>В.

2)Разностью 2-х векторов А-В, наз-ся век-р с=a+(-1)*b

3)Суммой неск-их векторов а и в наз. c=a+b, которые соед. начало а с концом в при условии, что начало в совп. с концом а.Св-ва: а+в=в+а; (а+в)+с=а+(в+с); а+0=а.

Теорема: 2 вектора а и в явл-ся коллинеарными тогда и только тогда, когда сущ-т число α такое, что а=α-в, в

3.Проекция вектора на ось.

Осью наз-ся прямая, у кот-й задано напр-е. Углом м-ду вект. а и осью l наз-ся угол, на который нужно повернуть в-р а, чтобы он по напр-ю совпал с осью.

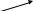
А’B’ – геометр. проекция в-ра AB на ось l.

Длина в-ра A’B’, взятая со зн. «+»,если напр-е в-ра A’B’ и оси совп и со зн «-», не совпадают наз-ся алгебраической проекцией в-ра АВ на ось l.

;

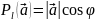
Св-ва проекций: 1)если в-р а=в, то ;2) =α =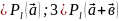

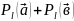
4.Базис. Координаты вектора.

Б азисом на прямой наз-ся некоторый ненулевой вектор. Базисом на плоскости н аз-ся упорядоченная пара ненулевых коллинеарных векторов на пл-ти. Базисом в пространстве наз. упорядоченныю тройку 3х некомпланарных векторов. Векторы наз. компланарными, если они лежат в 1-ой плоскости или в ||-ных плоскостях.

Любой вектор на плоскости может быть разложен по векторам базиса на плоскости. Любой вектор в пространстве может быть разложен по векторам базиса в пространстве.

ОС=OA+OB, OA=x*i, OB=j*y, OC=xi+yj. Числа х,у наз-ся координатами вектора ОС в данном базисе

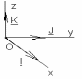
Длиной вектора называется арифметическое значение квадратного корня и скалярного квадрата.

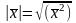
Теорема: Пусть (а,в) – базис на пл-ти, тогда любой в-р с, лежащий на пл-ти можно предст. в виде с=αа+βв.

Теорема: Пусть (а,в,с) – базис в пр-ве, тогда люб. в-р. d модет быть записан в виде: d= αа+βв+γc.

Св-ва коорд. в-ра. 1) Коорд. нул. в-ра в любом базисе = нули. 2) коорд. в-ра в зад. базисе опред-ны однозначно.3) При умн-и в-ра на число, его коорд. умн-ся на это число. 4) При сложении вект. их коорд, заданные в одном и том же базисе, складываются.