10.Сходимость ряда геометрической прогрессии.

В общем случае простой формулы для частичных сумм бесконечного ряда не существует, так что для установления сходимости или расходимости ряда прибегают к специальным методам. Например, если все члены ряда положительны, то можно показать, что ряд сходится, если каждый его член не превосходит соответствующего члена другого ряда, о котором известно, что он сходится. В принятых обозначения это можно записать следующим образом: если a_n і 0 и  сходится, то  сходится, если 0 Ј b_n Ј a_n. Например, так как ряд (4) сходится и

то можно сделать вывод, что ряд (8) тоже сходится. Сравнение представляет собой основной метод, позволяющий устанавливать сходимость многих рядов, сопоставляя их с простейшими сходящимися рядами. Иногда используют более специальные признаки сходимости (их можно найти в литературе по теории рядов.) Приведем еще несколько примеров сходящихся рядов с положительными членами:

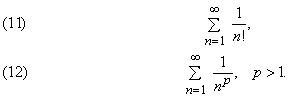
Сравнение можно использовать и для установления расходимости ряда. Если ряд   расходится, то и ряд  также расходится, если 0Ј b_n Ј a_n.

11.Положительные ряды. Необходимое и достаточное условие сходимости.

Положительный ряд сходится тогда и только тогда, когда последовательность его частичных сумм ограничена сверху.

Необходимое условие

Так как ряд сходится, то последовательность частичных сумм имеет предел. Следовательно она ограничена. А значит она ограничена и снизу и сверху. Доказано

Достаточное условие

Дан положительный ряд и последовательность частичных сумм ограничена сверху. Покажем, что наша последовательность(из членов ряда) неубывающая: S(n + 1) − S(n) = a(n + 1) Теперь используем свойство из теоремы о монотонной последовательности и получим, что последовательность частичных сумм сходится (она монотонно неубывает и ограничена сверху), следовательно ряд сходится (по определению).

12.Интегральный признак сходимости. Ряды Дирихле.

Ряд Абелева типа

Ряд  , где   и последовательность {a_n} — положительна и монотонна (начиная с некоторого места, хотя бы в широком смысле слова), называется рядом Абелева типа. Теорема (признак Дирихле сходимости рядов Абелева типа)

Пусть выполнены условия: Последовательность частичных сумм   ограничена, то есть  . . . Тогда ряд   сходится.

Признак Дирихле сходимости рядов Абелева типа является аналогом признака Дирихле о сходимости несобственного интеграла первого рода.

Легко убедиться, что признак Лейбница сходимости знакопеременных рядов является частным случаем этой теоремы, а именно:

сходимость ряда Лейбница на основании признака Дирихле.

Оценка остатка ряда Абелева типа Рассмотрим ряд   и пусть выполнены условия признака Дирихле. Тогда имеет место оценка:  .

13.Первый признак сравнения. Пример.

Пусть имеются два положительных ряда A= и B= , причём члены первого, начиная с некоторого места, не превосходят соответствующих членов второго: , n=m+1,m+2,…( )

Тогда из сходимости ряда B следует сходимость ряда A , а из расходимости ряда A следует расходимость ряда B .

Пример. Определить, сходится или расходится ряд  .

Решение. Воспользуемся признаком сравнения. Заметим, что 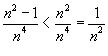  для всех натуральных n. Ряд  является обобщенным гармоническим рядом с p = 2 > 1 и, следовательно, сходится.  Таким образом, исходный ряд сходится по признаку сравнения.