
- •Курсовой проект
- •«Теория автоматического управления»
- •1. Составление динамической структурной схемы системы.
- •2. Составить дифференциальное уравнение и передаточную функцию замкнутой системы в общем виде при наличии и отсутствии кэ.
- •4. При помощи критерия Гурвица построить область устойчивости системы без кэ в плоскости коэффициента усиления разомкнутой системы и постоянной времени двигателя .
- •5. При значении коэффициента разомкнутой системы , найденном в п.3 и постоянной времени , принадлежащей границе устойчивости, построить кривую Михайлова,
- •6. Вводим кэ, так, чтобы радиус заданной области запаса устойчивости
- •7. Построение асимптотического лачх
- •9. Выполнить моделирование динамической структуры системы на эвм. Добиться наилучшего качества переходного процесса, изменяя постоянную времени корректирующего элемента.
5. При значении коэффициента разомкнутой системы , найденном в п.3 и постоянной времени , принадлежащей границе устойчивости, построить кривую Михайлова,
Для получения
аналитического выражения кривой
Михайлова подставим в полином
характеристического уравнения
![]() вместо
вместо
![]() получим:
получим:
 Кривая Михайлова
приведена на рис.4.
Кривая Михайлова
приведена на рис.4.
![]()
![]()
![]()
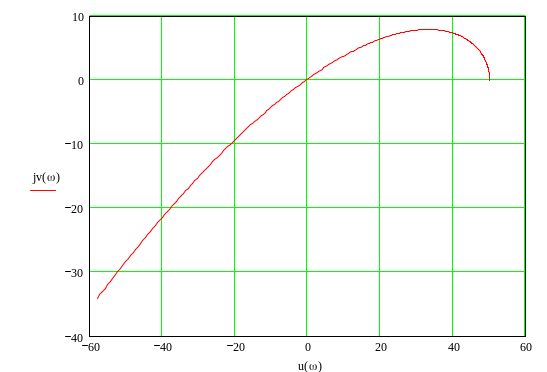
Рис.4. Кривая Михайлова при и постоянной времени , принадлежащей границе устойчивости.
6. Вводим кэ, так, чтобы радиус заданной области запаса устойчивости
Коэффициент статизма замкнутой системы по скорости возмущения с КЭ
![]()
Характеристическое уравнение системы с КЭ имеет вид:
![]()
Подставим числовые данные и получим:
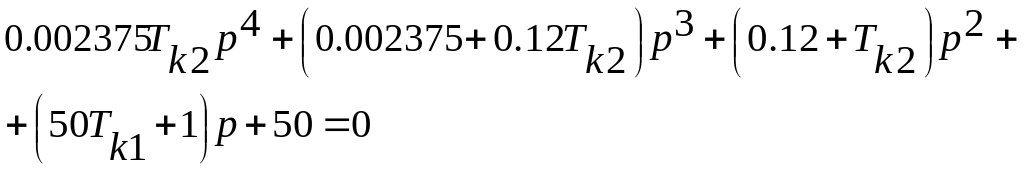
Выражение для кривой Михайлова:


Имеется две
неизвестных, найдем их из системы
уравнений и условия, что
![]() :
:
![]()
Учитывая, что
,
,
,
то
![]() ,
тогда
,
тогда
![]()
Найдем вещественные корни системы уравнения
![]()
![]()
![]()
![]()
![]()
![]()
Находим граничное
значение
![]() с, что является приемлемым значением
для
с, что является приемлемым значением
для
![]() цепочки.
цепочки.
Построим кривую Михайлова для трех случаев:
1).
![]() ;
;

2)
![]() ;
;

3)
![]()

Кривые Михайлова для трех случаев показаны на рис.5.
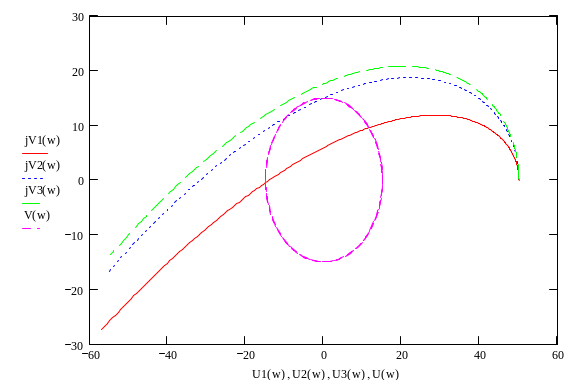
Рис.5. Кривые Михайлова системы с КЭ и область минимальной устойчивости.
Программа вычисления кривых Михайлова для трёх случаев и построение области устойчивости:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Исходя из этого
выбираем
![]() с.
с.
Тогда
![]() с.
с.
7. Построение асимптотического лачх
7.1. Построение асимптотического ЛАЧХ КЭ
Передаточная функция КЭ:
.
Асимптотическая ЛАЧХ образуется путем сложения двух функций:
1).
![]()
2).
![]()
График асимптотической ЛАЧХ корректирующего элемента изображен на рис.6.
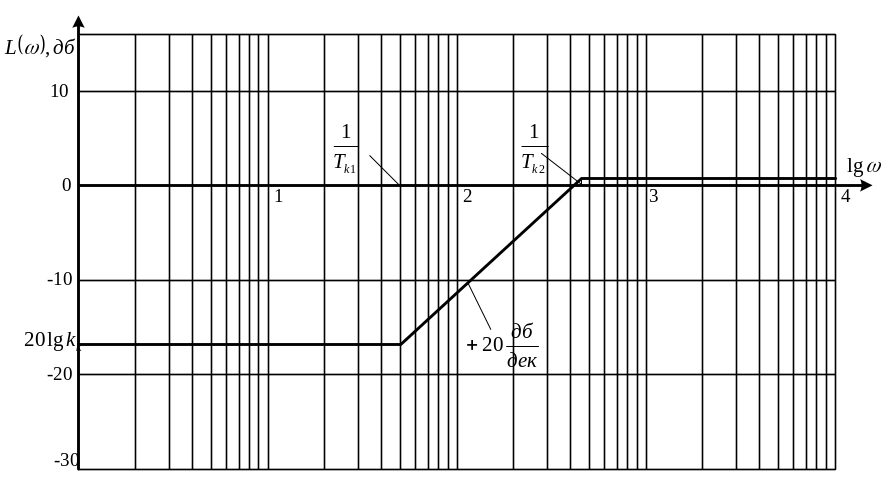 Рис.6.
Асимптотическая ЛАЧХ корректирующего
элемента
Рис.6.
Асимптотическая ЛАЧХ корректирующего
элемента
7.2. Построение асимптотической ЛАЧХ нескорректированной системы
Передаточная функция нескорректированной разомкнутой системы:
![]() .
.
Асимптотическая ЛАЧХ образуется путем сложения трех функций:
1). Апериодическое звено I
![]() .
.
2). Апериодическое звено II
![]() .
.
3). Интегрирующее звено
![]()
График асимптотической ЛАЧХ нескорректированной системы изображен на рис.7.

Рис.7. Асимптотическая ЛАЧХ нескорректированной системы
7.3. Построение асимптотической ЛАЧХ скорректированной системы
Передаточная функция скорректированной разомкнутой системы:
![]() .
.
Асимптотическая ЛАЧХ образуется путем сложения пяти функций:
1). Апериодическое звено I
.
2). Апериодическое звено II
![]() .
.
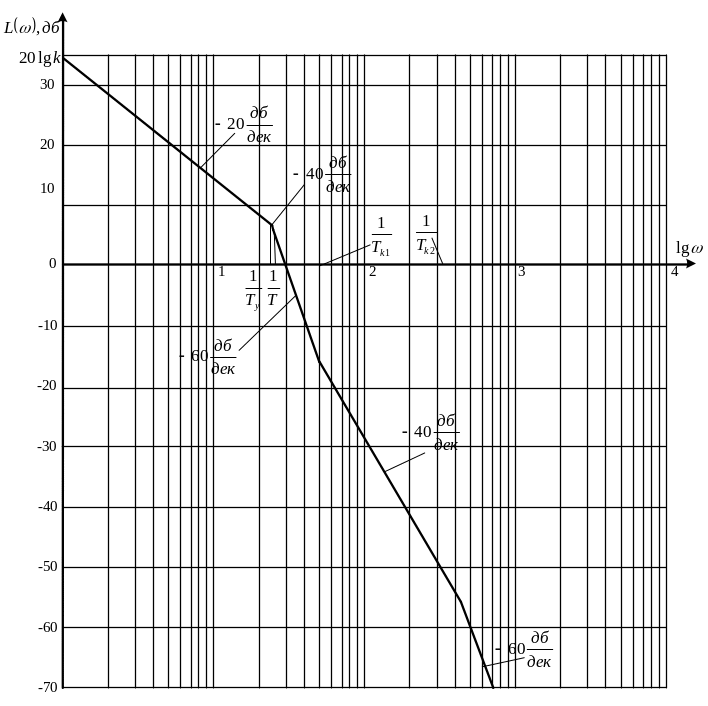
Рис.8. Асимптотическая ЛАЧХ скорректированной системы
3). Апериодическое звено III
![]() .
.
4). Интегрирующее звено
![]()
5). Дифференцирующее звено
![]()
График асимптотической ЛАЧХ скорректированной системы изображен на рис.8.
8. Ввести модель
исполнительного элемента нелинейное
звено (звено с зоной нечувствительности)
с коэффициентом усиления
![]() на линейном участке. Определить при
каких значениях параметра
на линейном участке. Определить при
каких значениях параметра
![]() в системе возникают устойчивые
автоколебания. Оценить влияние этого
параметра на частоту и амплитуду
автоколебаний.
в системе возникают устойчивые
автоколебания. Оценить влияние этого
параметра на частоту и амплитуду
автоколебаний.
Характеристика нелинейного элемента представлена на рис.9.
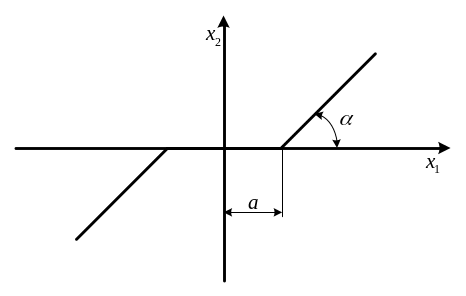
Рис.9. Статическая характеристика нелинейного элемента
|
1 |
2 |
3 |
4 |
5 |
6 |
|
|
2,6 |
2 |
1,6 |
1,5 |
1,4 |
Для определения амплитуды и частоты автоколебаний используем метод Гольдфарба (рис.10).
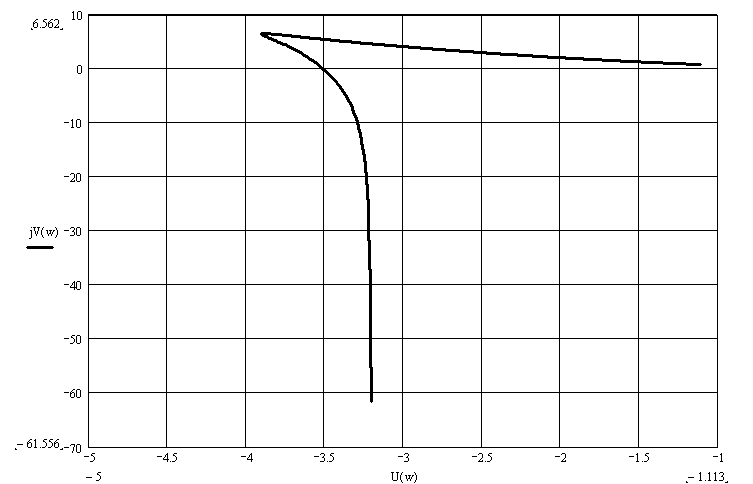
Рис.10. Определение автоколебаний
![]()
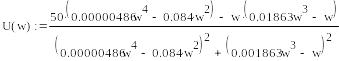
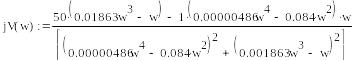
Как видно из рис.10
устойчивых автоколебаний в системе
возникают при
![]() ,
частота
,
частота
![]() =7
рад/с.
=7
рад/с.
