6.3. Непрерывность функций на интервале, полуинтервале, отрезке

Определение 6.4.

Функция f(x) называется непрерывной на интервале (a,b), если она непрерывна в каждой точке этого интервала. Обозначают f(x)∈C(a,b).

Определение 6.5.

Функция f(x) называется непрерывной на полуинтервале [a,b), (или (a,b]), если она непрерывна на интервале (a,b) и непрерывна справа в точке a (или непрерывна слева в точке b). Пишутf(x)∈C[a,b) (или f(x)∈C(a,b]).

Определение 6.6.

Функция f(x) называется непрерывной на отрезке [a,b], если она непрерывна на интервале (a,b),непрерывна справа в точке a и непрерывна слева в точке b. Обозначают f(x)∈C[a,b].

Теорема 6.7. 

Каждая основная элементарная функция непрерывна в области определения.

Д о к а з а т е л ь с т в о.

Доказательство следует из  теоремы 6.4 и  определений 6.4-6.6.

■

6.4. Свойства функций, непрерывных на отрезке

Свойство 6.1. 

Функция, непрерывная на отрезке, ограничена на нём.

Свойство 6.2. 

Функция f(x), непрерывная на отрезке [a,b], принимает на нем наибольшее и наименьшее значения, т.е. существуют такие точки ξ η отрезка [a,b], что f(ξ)=m, f(η)=M, и для всех точек x этого отрезка выполняются неравенства m≤f(x)≤M.

Свойство 6.3. 

Если функция f(x) непрерывна на отрезке [a,b] и f(a)=A, f(b)=B, причем A≠B, то для любогоC такого, что A<C<B, найдется точка ξ∈(a,b) такая, что f(ξ)=C.

Как следствие из  свойства 6.3 получаем: если функция f(x) непрерывна на отрезке [a,b] и принимает на его концах значения разных знаков, то найдётся такая точка ξ∈(a,b), что f(ξ)=0, Точка ξ в которойf(ξ)=0, называется нулём функции f(x).

Теорема 6.8. 

Пусть функция y=f(x) строго монотонна (возрастает или убывает) и непрерывна на отрезке [a,b].Тогда обратная функция x=f−1(y) определена, строго монотонна (возрастает или убывает) и непрерывна на соответствующем отрезке оси Oy.

6.5. Точки разрыва функций и их классификация

Согласно  определению 6.1 для функции f(x), непрерывной в точке x0, должны выполняться три условия непрерывности:

1) функция определена в точке x0 (∃f(x0));

2) функция имеет конечный предел при x→x0 (∃ конечный предел limx→x0f(x));

3) предел функции при x→x0 равен значению функции в самой точке x0 (limx→x0f(x)=f(x0)).

Определение 6.7.

Точка x0 называется точкой разрыва функции f(x), а сама функция разрывной в точке x0, если она не является непрерывной в этой точке, т.е. нарушено хотя бы одно из указанных выше условий: либоx0∉Df, либо не существует конечного предела limx→x0f(x), либо limx→x0f(x)≠f(x0).

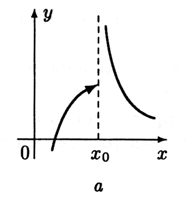
Рассмотрим функции, заданные графически на рис. 6.5. Для всех этих функций x0 — точка разрыва.

Таблица 

Рис. 6.5a

Рис. 6.5b

Рис. 6.5c

В первом случае (рис. 6.5, а) не выполнено условие 1, так как в точке x0 функция не определена.

Во втором случае (рис. 6.5, б) нарушено ксловие 2, так как предел limx→x0f(x) не существует.

В третьем случае (рис. 6.5, в) не выполнено условие 3, так как limx→∞f(x)=A≠f(x0).

Определение 6.8.

Пусть x0 — точка разрыва функции f(x). Точка x0 называется точкой разрыва первого рода, если функция имеет в этой точке пределы справа и слева, т.е.

limx→x+0f(x)=f(x+0)≠∞    и    limx→x−0f(x)=f(x−0)≠∞.

В этом случае либо f(x+0)≠f(x−0), либо f(x+0)=f(x−0)≠f(x0), причем f(x) может быть и не определена в точке x0.

Разность f(x+0)−f(x−0) называют скачком функции f(x) в точке x0.

Определение 6.9.

Точка разрыва первого рода x0, в которой f(x+0)=f(x−0), называется точкой устранимого разрыва.

Рассмотрим функцию f(x)=xsin1x, для которой x=0 есть точка разрыва, так как функция не определена в этой точке. Односторонние пределы функции в этой точке конечны и равны, посколькуf(+0)=limx→+0xsin1x=0, f(−0)=limx→−0xsin1x=0. Следовательно, x=0 — точка устранимого разрыва. Полагая f(0)=f(+0)=f(−0)=0, получим функцию, непрерывную в точке x=0:

ϕ(x)=⎧⎩⎨xsin1x,          0,x≠0;x=0.

Тем самым мы доопределили по непрерывности данную функцию f(x).

Определение 6.10.

Точка разрыва x0, не являющаяся точкой разрыва первого рода, называется точкой разрыва второго рода. В этом случае хотя бы один из односторонних пределов функции в точке x0 не существует или равен бесконечности.

Замечание 6.2.

Принимая во внимание  замечание 6.1 и  определение 6.7, подчеркнем еще раз: для того, чтобы функция f(x) балы непрерывной в точке x0 необходимо и достаточно вполнение условий:

1) функция f(x) определена в точке x0 (∃ f(x0));

2) cуществуют конечные односторонние пределы функции в этой точке(∃f(x+0)≠∞, ∃f(x−0)≠∞);

3) односторонние пределы функции в точке x0 равны значению функции в этой точке(f(x+0)=f(x−0)=f(x0)).

Поэтому при исследовании функции на непрерывность и определении точек разрыва функции рекомендуется придерживаться следующей схемы.

1 Найти область определения функции.

2 Указать промежутки области определения функции, на которых функция непрерывна.

3 Выявить точки, в которых может быть нарушена непрерывность функции.

4 Найти односторонние пределы функции в каждой из указанных точек. Если функция определена в них, то найти значения функции в этих точках.

5 Сравнить в каждой такой точке односторонние пределы и значение функции, если она определена в этой точке, и установить либо непрерывность, либо разрыв функции в каждой из полученных точек.

6 В случае разрыва функции определить тип точки разрыва.

6.6. Типовые примеры

Задача 1.

Найти односторонние пределы в точке x0=1 функции

f(x)={    x+1,3x+2,0≤x<1;1<x<3.

Р е ш е н и е.

 Найдем правый предел f(1+0) функции f(x) в точке x0=1, т.е. при x→1 и x>1. Имеем

f(1+0)=limx→1+0f(x)=limx→1+0(3x+2)=5.

Для левого предела f(1−0) в точке x0=1 (x→1,x<1) получим

f(1−0)=limx→1−0f(x)=limx→1−0(x+1)=2.

■

Задача 2.

Найти точки разрыва функции f(x)=∣∣x∣∣x и определить тип каждой точки разрыва.

Р е ш е н и е.

 Точка x0=0 является точкой разрыва функции, так как в ней функция не определена. Найдем правый и левый пределы функции в этой точке:

f(+0)=limx→+0|x|x=limx→+0xx=1;

f(−0)=limx→−0|x|x=limx→−0−xx=−1.

Односторонние пределы конечны и различны, точка x0=0 — точка разрыва первого рода. На графике (рис. 6.6) виден конечный скачок функции в точке x0=0, равный f(+0)−f(−0)=2.

■

Рис. 6.6

Рис. 6.7

Задача 3.

Найти точки разрыва функции f(x)=sinxx и определить тип каждой точки разрыва.

Р е ш е н и е.

 В точке x0=0 функция не определена, т.е. x0 — точка разрыва функции. Найдем правый и левый пределы функции в этой точке:

f(+0)=limx→+0sinxx=1;

f(−0)=limx→−0sinxx=1.

Так как односторонние пределы конечны и равны, т.е. f(+0)=f(−0), то x0=0 — точка устранимого разрыва данной функции (рис. 6.7). Если положить f(0)=1, то разрыв можно устранить. Тем самым первоначальную функцию доопределим по непрерывности в точкеx0=0. Аналитически новую функцию ϕ(x), непрерывную на всей числовой оси, запишем в виде

ϕ(x)=⎧⎩⎨ sinxx,        1,x≠0;x=0.

■

Задача 4.

Исследовать на непрерывность функцию

f(x)=⎧⎩⎨⎪⎪ x3+2,2,1,x>0;x<0;x=0.

Р е ш е н и е.

 Функции y1=x3+2 и y2=2 непрерывны при любом x. Единственной точкой, в которой функция f(x) может иметь разрыв, является точка x=0. Вычислим односторонние пределы функции f(x) в этой точке:

f(+0)=limx→+0f(x)=limx→+0(x3+2)=2;

f(−0)=limx→−0f(x)=limx→−02=2.

Так как f(0)=1≠f(+0)=f(−0)=2, то x=0 — точка разрыва первого рода данной функции (рис. 6.8).

■

Задача 5.

Исследовать на непрерывность функцию f(x)=sin1x.

Р е ш е н и е.

 Данная функция непрерывна всюду, кроме точки x0=0. Рассмотрим f(+0)=limx→+0sin1x. Так как 1x→+∞ при x→+0 и значения функции f(x) колеблются между −1 и +1, не приближаясь к какому-либо определенному значению, то f(+0) не существует. Аналогично, не существует и f(−0). Следовательно, x=0 — точка разрыва второго рода (рис. 3.11).

■

Задача 6.

Исследовать на непрерывность функцию f(x)=xx2−4.

Р е ш е н и е.

 Данная рациональная функция непрерывна всюду, кроме точек, где знаменатель обращается в ноль. Следовательно, функция терпит разрыв в точках x1=2 и x2=−2. Найдем односторонние пределы данной функции в этих точках:

f(2+0)=limx→2+0xx2−4=+∞;

f(2−0)=limx→2−0xx2−4=−∞;

f(−2+0)=limx→−2+0xx2−4=+∞,

f(−2−0)=limx→−2−0xx2−4=−∞.

Точки x1=2 и x2=−2 — точки разрыва второго рода (рис. 6.9).

■

Рис. 6.8

Рис. 6.9

Рис. 6.10

Задача 7.

Исследовать на непрерывность в точке x0=0 функцию f(x)=∣∣sinx∣∣2x.

Р е ш е н и е.

 В точке x0=0 функция не определена. Следовательно, x0=0 — точка разрыва функции. Найдем односторонние пределы функции в этой точке. Если x→0 и x>0, то ∣∣sinx∣∣2x>0 иf(+0)=limx→+0∣∣sinx∣∣2x=12. Если x→0 и x<0, то ∣∣sinx∣∣2x<0 и f(−0)=limx→−0∣∣sinx∣∣2x=−12. Так как односторонние пределы f(+0) и f(−0) конечны и различны, то x0=0 — точка разрыва первого рода, причем скачок функции в этой точке равен f(+0)−f(−0)=12−(−12)=1(рис. 6.10).

■

Задача 8.

Исследовать на непрерывность функцию

f(x)={x2,2x−1,−1≤x<2;2≤x≤3.

Р е ш е н и е.

 Функция f(x) определена всюду на [−1,3], непрерывна на полуинтервале [−1,2) и на отрезке[2,3]. Единственной точкой, в которой возможен разрыв функции f(x) является точка x0=2.Вычислим односторонние пределы функции f(x) в этой точке

f(2−0)=limx→2−0x2=4,

f(2+0)=limx→2+0(2x−1)=3.

Односторонние пределы f(2−0) и f(2+0) конечны и различны. Следовательно, x0=2 — точка разрыва первого рода. Скачок функции в точке x0=2 равенf(2+0)−f(2−0)=3−4=−1 (рис. 6.11).

■

Рис. 6.11

Рис. 6.12

Задача 9.

Найти и исследовать точки разрыва функции f(x)=sinxx2+2x.

Р е ш е н и е.

 Точками разрыва функции f(x) будут точки x1=0 и x2=−2 в которых функция f(x) не определена (x2+2x=0). Исследуем точку x1=0. При x→0 и x>0 функция sinx>0,sinxx(x+2)>0, f(+0)=limx→+0sinxx2+2x=limx→+0sinxx(x+2)=12. При x→0 и x<0 функция sinx<0,sinxx(x+2)>0, f(−0)=limx→−0sinxx2+2x=limx→−0sinxx(x+2)=12. Односторонние пределы f(+0) иf(−0) в точке x1=0 конечны и равны. Следовательно, x1=0 — точка устранимого разрыва. Разрыв устраняется, если положить f(0)=12. Рассмотрим точку x2=−2. Еслиx→−2 и x>−2, то sinx<0, x<0, x+2>0, sinxx(x+2)>0 иf(−2+0)=limx→−2+0sinxx(x+2)=+∞. Если x→−2 и x<−2, то sinx<0, x<0, x+2<0,sinxx(x+2)<0 и f(−2−0)=limx→−2−0sinxx(x+2)=−∞. Следовательно, x2=−2 — точка разрыва второго рода (рис. 6.12).

■

Задача 10.

Исследовать на непрерывность функцию f(x)=e1x+3.

Р е ш е н и е.

 Данная функция непрерывна всюде, кроме точки x0=−3. Найдем односторонние пределыf(−3+0) и f(−3−0) Если x→−3 и x>−3, то x+3>0, 1x+3→+∞ иf(−3+0)=limx→−3+0e1x+3=+∞ Если x→−3 и x<−3, то x+3<0, 1x+3→−∞ иf(−3−0)=limx→−3−0e1x+3=0. Следовательно, точка x0=−3 — точка разрыва второго рода (рис. 6.13).

■

Рис. 6.13

Рис. 6.14

Задача 11.

Исследовать на непрерывность функцию f(x)=12−21/x.

Р е ш е н и е.

 Данная функция непрерывна всюду, кроме точек x1=0 и x2=1, так как в точке x1=0 не определена дробь 1x в точке x2=1 знаменатель 2−21/x исходной дроби равен нулю. Найдем односторонние пределы данной функции в точках x1 и x2 При x→0 и x>0 дробь 1x→+∞,21/x→+∞ и f(+0)=limx→+012−21/x=0. При x→0 и x<0 дробь 1x→−∞, 21/x→0 иf(−0)=limx→−012−21/x=12. Так как в точке x1=0 односторонние пределы f(+0)=0 иf(−0)=12 конечны и различны, то x1 — точка разрыва первого рода. Найдем f(1+0) иf(1−0). При x→1 и x>1 дробь 1x<1, 21/x<2, разность 2−21/x→0, оставаясь положительной. Поэтому f(1+0)=limx→1+012−21/x=+∞. При x→1 и x<1 дробь 1x>1,21/x>2, разность 2−21/x→0, оставаясь отрицательной, иf(1−0)=limx→1−012−21/x=−∞. Следовательно, x2=1 — точка разрыва второго рода (рис. 6.14).

■