1. Ма́трица — математический объект, записываемый в виде прямоугольной таблицы элементов кольца или поля (например, целых или комплексных чисел), которая представляет собой совокупность строк и столбцов, на пересечении которых находятся её элементы. Количество строк и столбцов матрицы задают размер матрицы. Хотя исторически рассматривались, например, треугольные матрицы, в настоящее время говорят исключительно о матрицах прямоугольной формы, так как они являются наиболее удобными и общими.

Определи́тель — одно из основных понятий линейной алгебры. Определитель матрицы является многочленом от элементов квадратной матрицы (то есть такой, у которой количество строк и столбцов равно). В общем случае матрица может быть определена над любым коммутативным кольцом, в этом случае определитель будет элементом того же кольца.

Минором порядка k матрицы А называется определитель, составленный из элементов, стоящих на пересечении любых k строк и k столбцов данной матрицы.

Алгебраическим дополнением минора матрицы называется его дополнительный минор, умноженный на (-1) в степени, равной сумме номеров строк и номеров столбцов минора матрицы.

2. Свойства определителей

- Если две строки (столбца) матрицы совпадают, то её определитель равен нулю.

- Если две (или несколько) строки (столбца) матрицы линейно зависимы, то её определитель равен нулю.

- Если переставить две строки (столбца) матрицы, то её определитель умножается на (-1).

- Общий множитель элементов какого-либо ряда определителя можно вынести за знак определителя.

- Если хотя бы одна строка (столбец) матрицы нулевая, то определитель равен нулю.

- Сумма произведений всех элементов любой строки на их алгебраические дополнения равна определителю.

- Сумма произведений всех элементов любого ряда на алгебраические дополнения соответствующих элементов параллельного ряда равна нулю.

- Определитель произведения квадратных матриц одинакового порядка равен произведению их определителей формула Бине-Коши).

Правило разложения определителя по строке (столбцу).

Для матрицы первого порядка детерминантом является сам единственный элемент этой матрицы:

Для матрицы детерминант определяется как

Для матрицы определитель задаётся рекурсивно:

, где — дополнительный минор к элементу a1j. Эта формула называется разложением по строке.

В частности, формула вычисления определителя матрицы такова:

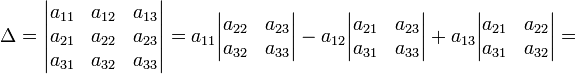
= a11a22a33 − a11a23a32 − a12a21a33 + a12a23a31 + a13a21a32 − a13a22a31

Легко доказать, что при транспонировании определитель матрицы не изменяется (иными словами, аналогичное разложение по первому столбцу также справедливо, то есть даёт такой же результат, как и разложение по первой строке)

3. Системы линейных уравнений

Система m линейных уравнений с n неизвестными (или, линейная система) в линейной алгебре — это система уравнений вида

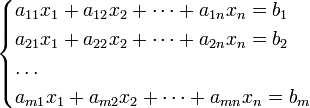
Здесь x1, x2, …, xn — неизвестные, которые надо определить. a11, a12, …, amn — коэффициенты системы — и b1, b2, … bm — свободные члены — предполагаются известными. Индексы коэффициентов (aij) системы обозначают номера уравнения (i) и неизвестного (j), при котором стоит этот коэффициент, соответственно[1].

- Система называется однородной, если все её свободные члены равны нулю (b1 = b2 = … = bm = 0), иначе — неоднородной.

- Система называется квадратной, если число m уравнений равно числу n неизвестных.

- Решение системы — совокупность n чисел c1, c2, …, cn, таких что подстановка каждого ci вместо xi в систему обращает все её уравнения в тождества.

- Система называется совместной, если она имеет хотя бы одно решение, и несовместной, если у неё нет ни одного решения.

- Совместная система вида может иметь одно или более решений.

Решения c1(1), c2(1), …, cn(1) и c1(2), c2(2), …, cn(2) совместной системы вида (1) называются различными, если нарушается хотя бы одно из равенств: c1(1) = c1(2), c2(1) = c2(2), …, cn(1) = cn(2).

- Совместная система вида называется определённой, если она имеет единственное решение; если же у неё есть хотя бы два различных решения, то она называется неопределённой. Если уравнений больше, чем неизвестных, она называется переопределённой.

Обычно ранг матрицы A обозначается ( ) или .

Пример: Делим первую строку на 3.

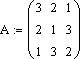
Теперь вычитаем из второго и третьего столбца первый с коэффициентами 2/3 и 1/3 соответственно.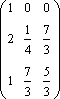

Вычитаем из второй и третьей строки первую с коэффициентами 2 и 1 соответственно.

и т.д. В итоге получим матрицу: 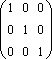Следовательно ранг матрицы равен 3.