П 14. Вычисление площадей плоских фигур

14.1. Вычисление площадей плоских фигур в декартовых координатах

Пусть функция задана на отрезке .

Рассмотрим множество точек ,

которое можно истолковать как криволинейную трапецию .

Необходимо найти площадь этой криволинейной трапеции.

Исходя из определения определенного интеграла и его геометрического смысла, в том случае, когда площадь криволинейной трапеции равна

П р и м е р. Найдите площадь фигуры, ограниченной линиями

Р е ш е н и е. Построим фигуру, ограниченную указанными линиями.

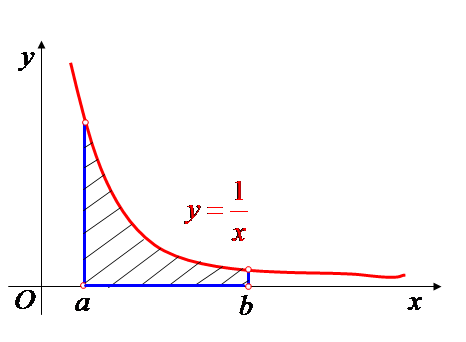
Площадь заданной фигуры вычислим по формуле (1)

Пусть функции и заданы на отрезке . Рассмотрим множество точек ,

которое можно истолковать как фигуру .

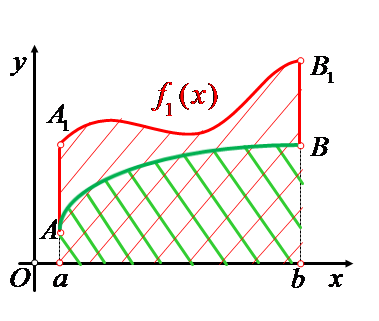
Площадь фигуры можно рассматривать как разность площадей

криволинейной трапеции и криволинейной трапеции

.

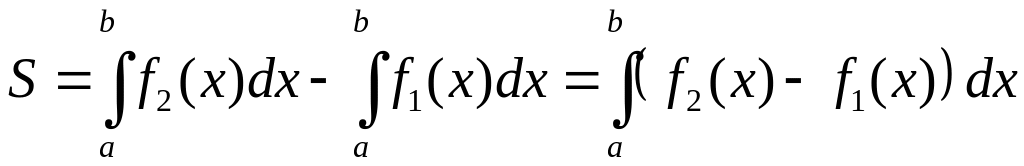14.2. Вычисление площадей плоских фигур в полярных координатах

Пусть положение любой точки на плоскости однозначно определяется двумя числами , где .

Пусть неотрицательная, непрерывная на отрезке функция, .

Рассмотрим множество точек

,

которое можно истолковать как криволинейный треугольник

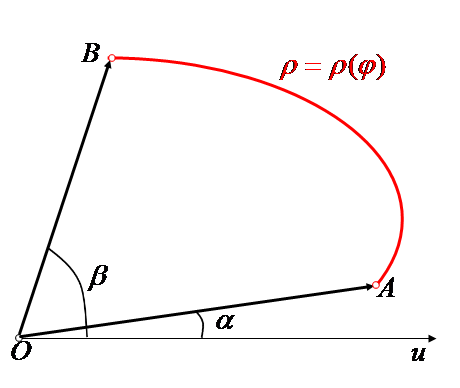
Для вычисления площади криволинейного треугольника разобьём этот треугольник на элементарные криволинейные треугольники.

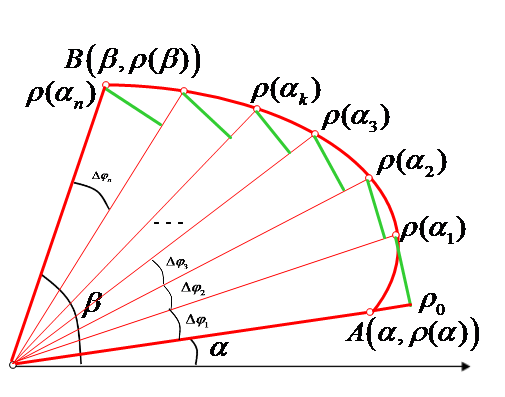
Элементарные криволинейные треугольники заменим прямоугольными треугольниками.

Высоты этих треугольников положим равными ,

а основания соответственно – .

Площадь -го элементарного треугольник очевидно будет равна

.

Площадь криволинейного треугольника будет приближённо равна

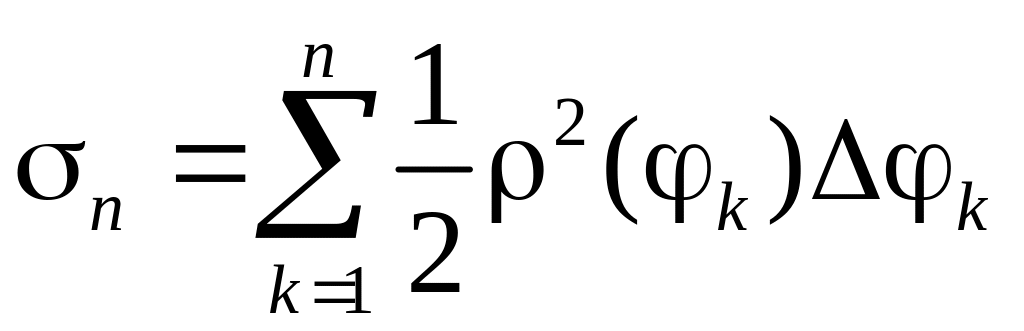. (1)

Выражение (1) можно рассматривать как интегральную сумму для функции на отрезке .

Введём обозначение . – это мелкость

разбиения .

Тогда площадь криволинейного треугольника

получим при переходе в выражении (1) к пределу при

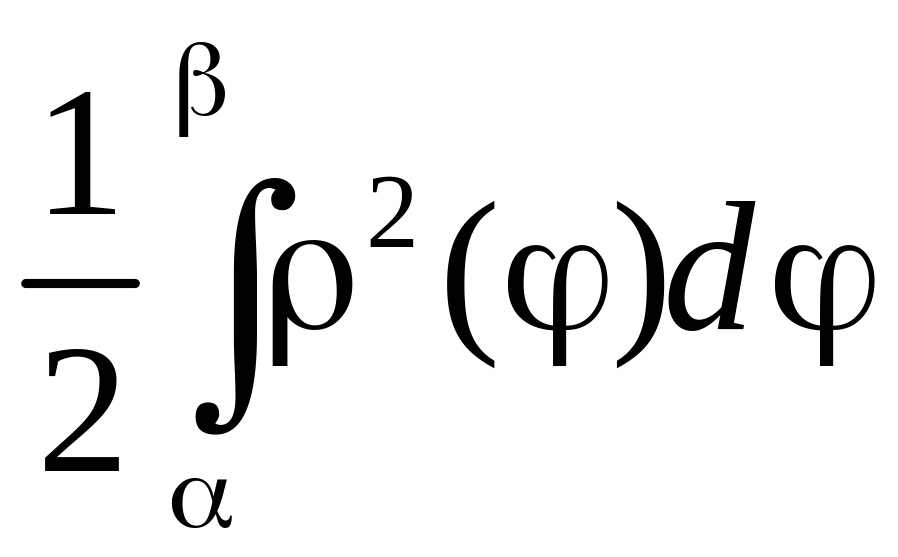= . (2)

Итак, площадь плоской фигуры в полярной системе координат равна

.

П р и м е р. Вычислите площадь фигуры, ограниченной кривой (кардиоидой)

.

Р е ш е н и е. Изобразим график кардиоиды

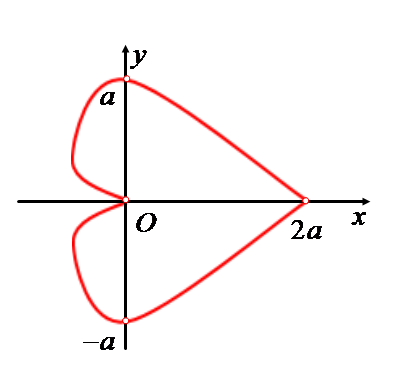
Как видим, кардиоида представляет собой линию, симметричную относительно оси .

Поэтому

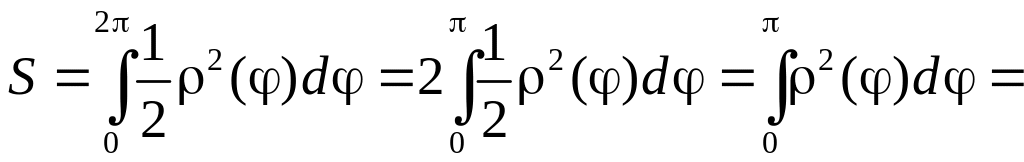
П 15. Вычисление длины кривой

Пусть кривая задана параметрически

, .

Разобьем отрезок на частей точками .

Обозначим через соответствующие точки на кривой . Соединим эти точки прямыми.

Полученную при этом ломанную называют ломанной, вписанной в кривую .

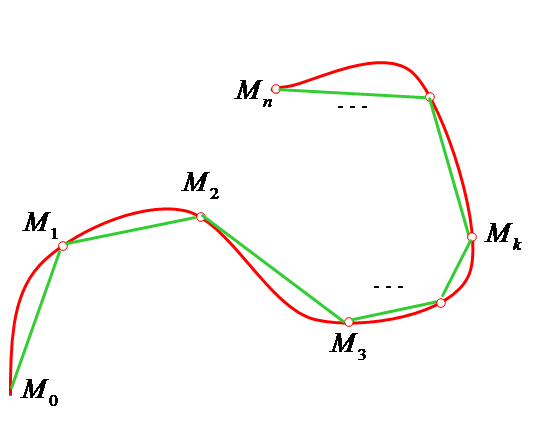
Длину элементарного звена равна

Длина ломанной в таком случае будет равна

. (1)

Обозначим через . Тогда длину кривой получим, перейдя в выражении (1) к пределу при

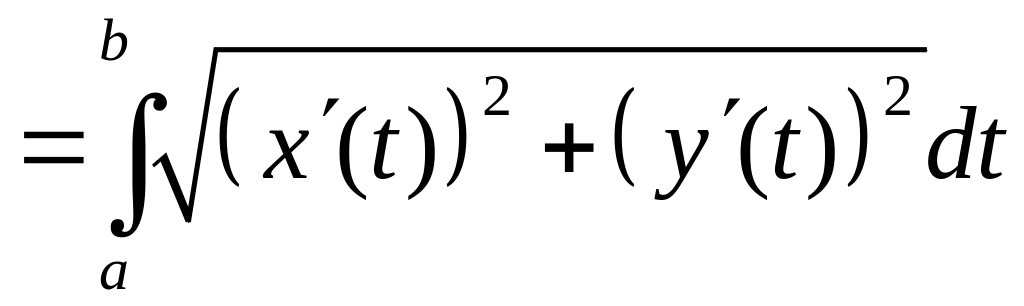. (2)

Итак, длина кривой согласно выражению (2) определяется формулой

. (3)

Длина пространственной кривой , заданной параметрически

, ,

будет равна

.

Если плоская кривая задана в явном виде

, ,

то параметрические уравнения кривой

можно в этом случае представить в виде

, , .

В результате выражении (3) получается в виде

.

П р и м е р. Найти длину кривой, заданной параметрически .

Р е ш е н и е. Построим график заданной кривой

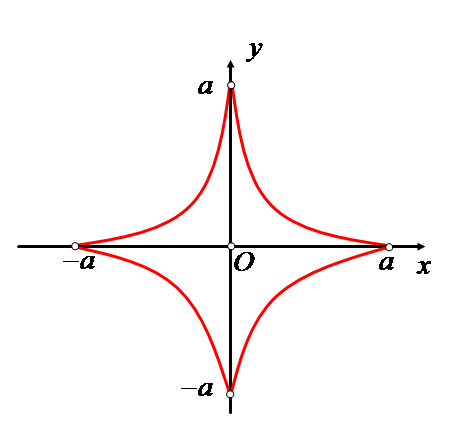
Так как кривая симметрична относительно координатных осей, то достаточно найти .

Поэтому длина кривой будет равна

.
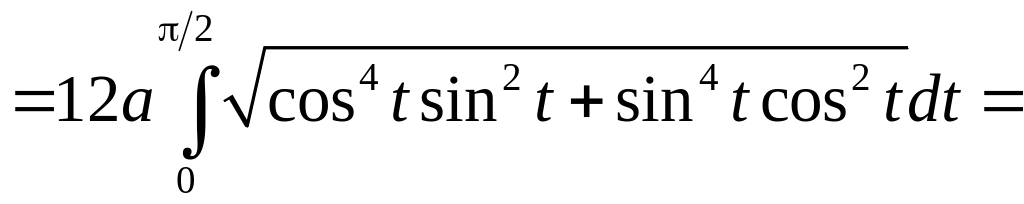
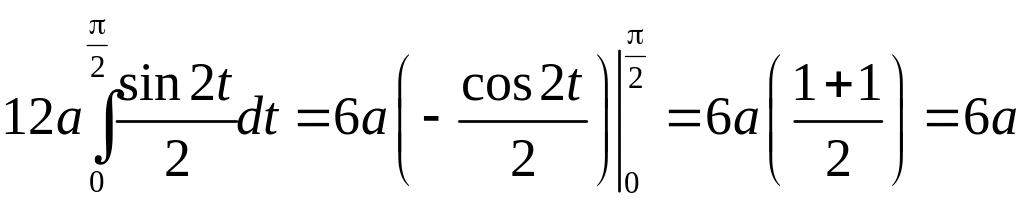