Механизм, предназначенный для передачи вращательного движения от одного вала к другому с помощью находящихся в зацеплении зубчатых зубчатых колес, называют зубчатой передачей. Зубчатые передачи могут быть с внешним и внутренним зацеплением. Наиболее распространены передачи с внешним зацеплением.

Достоинства:

1. Возможность передачи практически любых мощностей ( до 50 000 кВт и более) при весьма широком диапазоне окружных скоростей (от долей м/с до 30…150 м/с). При высоких скоростях применяют передачи с косыми зубьями, изготовленные с высокой точностью и тщательно смонтированные. Обычно для передач с косыми или криволинейными зубьями _мах=30…35 м/с. 2. Постоянство передаточного отношения. 3. Компактность, надежность и высокая усталостная долговечность передачи. 4. Высокий КПД ( =0,97…0,99) при высокой точности изготовления и монтажа, низкой шероховатости рабочей поверхности зубьев, жидкой смазке и передаче полной мощности. 5. Простота обслуживания и ухода. 6. Сравнительно небольшие силы давления на валы и их опоры. 7. Может быть изготовлена из самых разнообразных материалов, металлических и неметаллических.

Недостатки:

1. Ограниченность передаточного отношения. Передаточное число – это не что иное как отношение числа зубьев ведомой шестерни к числу зубьев ведущей (коробка переключения передач или редуктора). На практике это выглядит следующим образом. Если одна (ведомая) шестерня имеет 60 зубьев, а другая (ведущая) – 30, то передаточное число данной пары равно 2 (60:30). Передаточное число – одна из основных характеристик зубчатых передач, которые обеспечивают передачу крутящего момента от двигателя на привод какого-либо другого устройства (узла). При этом данный механизм позволяет увеличивать или уменьшать величину передаваемого момента. Например, изменяя число зубцов на обеих шестернях, можно увеличивать или уменьшать передаваемый от двигателя к «потребителю» крутящий момент. Передаточным отношением называется отношение числа зубьев ведущего колеса к числу зубьев ведомого, обозначается оно буквой i в отличие от передаточного числа, обозначаемого 1/i.

2. Является источником вибрации и шума, особенно при низком качестве изготовления и монтажа и значительных скоростях. 3. При больших перегрузках возможна поломка деталей (пробуксовки исключены). 4. Относительная сложность изготовления высокоточных зубчатых колес.

По применению и распространению в различных областях народного хозяйства зубчатые передачи по праву занимают первое место. В любой отрасли машиностроения, приборостроения, на транспорте, в связи зубчатые передачи находят широкое применение: автомобили, тракторы, самолеты, турбоэлектроды, станки, электронно-вычислительные и счетно-решающие машины, электросчетчики, часы, измерительные приборы и т.д.

Зубчатые передачи классифицируются: а) по конструктивному оформлению: открытые, не имеющие защитного кожуха и масляной ванны; полуоткрытые, имеющие защитный кожух; закрытые, имеющие картер и крышку, хорошо изолирующие передачу от внешней среды;б) по окружной скорости: тихоходные ( _мах=3…4 м/с); среднескоростные ( 4 м/с 15 м/с); высокоскоростные ( 15 м/с); в) по взаимному расположению осей валов: при валах с параллельными осями- цилиндрические ( прямозубые, шевронные, косозубые); при валах с пересекающимися осями- конические( прямозубые и косозубые, или с криволинейными зубьями); при валах со скрещивающимися осями- винтовые, гипоидные.

Цилиндрические зубчатые передачи

Зубчатые колеса для параллельных валов называют цилиндрическими. Одно из двух входящих в зацепление зубчатых колес – передающее движение – является ведущим, другое – ведомым. Если одно из колес значительно меньше другого, оно называется шестерней. Если отношение частот вращения ведущего и ведомого колес равно единице, то оба зубчатых колеса имеют одинаковые размеры. Передаточное отношение равно отношению чисел зубьев двух колес. Например, шестерня с 10 зубьями вращается в 4 раза быстрее сцепленного с ней зубчатого колеса, имеющего 40 зубьев. Зубья могут быть расположены как на наружной, так и на внутренней поверхности колеса. При наружном зацеплении колеса вращаются в противоположных направлениях, при внутреннем – в одном.

Виды цилиндрических зубчатых передач

Цилиндрические зубчатые передачи бывают прямозубые, косозубые и шевронные (рис. 1).

Зубчатые колеса, зубья которых параллельны оси колеса, называются прямозубыми. Для увеличения контактной длины и числа зубьев, находящихся в зацеплении (что необходимо для передачи большего момента и более плавной работы на повышенных частотах вращения), применяют косозубые зубчатые колеса. Серьезным недостатком косозубых колес является осевое усилие, возникающее в контакте зацепленных зубьев. Для его устранения применяются шевронные зубчатые колеса с V-образными (угловыми) косыми зубьями.

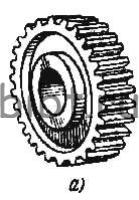
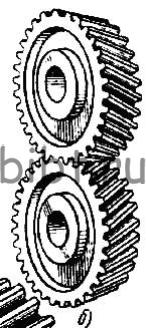
Рис. 1.Цилиндрические зубчатые колеса:а — прямозубое, б — косозубые, в — шевронное

Кинематическая схема и основные геометрические соотношения

Рассмотрим на примере прямозубой цилиндрической зубчатой передачи.

Зубчатая передача, в которой образующие боковых поверхностей зубьев параллельны образующим делительного цилиндра шестерни и колеса, называется прямозубой цилиндрической.

На рис.2 показаны цилиндрические прямозубые передачи внешнего (а) и внутреннего (б) зацепления.

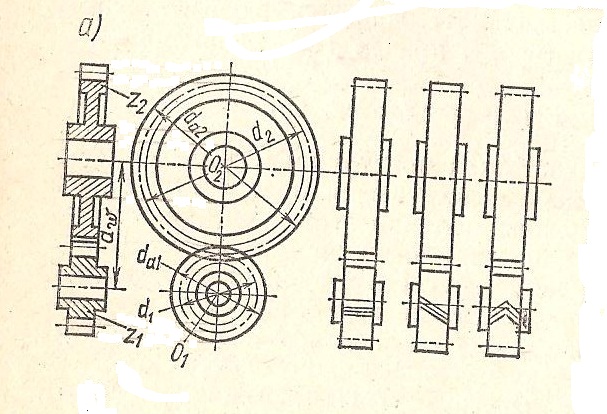
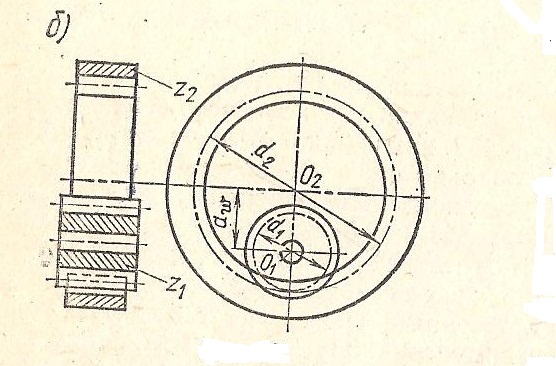
Рис. 2

Основные геометрические соотношения прямозубой цилиндрической передачи следующие (рис.3):

• Делительный диаметр(диаметр окружности, по которой обкатывается инструмент при нарезании) d=mz; является также начальным, т.к. у передач без смещения (при нарезании колес со смещением делительная плоскость рейки(делительная окружность инструмента) смещается к центру или от центра заготовки)начальные и делительные окружности совпадают d =d

• Pасчетный модуль(модуль) m=m_t=p/ =d/z, где р- расчетный шаг(шаг). Расстояние между одноименными профилями двух соседних зубьев, взятое по дуге делительной(основной) окружности, называется окружным шагом по делительной р_t или основной p_b окружностям. Между р_t и p_b существует зависимость p_b= р_tcos .z- число зубьев. -угол профиля зуборезного инструмента равен 20⁰.

m-модуль зацепления является основным параметром для расчета элемента колес, имеет стандартный ряд значений, измеряется в мм, основная характеристика размеров зубьев.

• Коэффициент высоты зуба f= h_a/m=1, где h_a= m, h_f=1,25m, h_f может быть и больше и меньше 1,25m; с=0,25 m- радиальный зазор.

h_a-высота головки зуба(часть профиля зуба, ограниченная делительной окружностью и окружностью выступов), h_f-высота ножки зуба(часть профиля зуба, ограниченная делительной окружностью и окружностью впадин)

полная высота зуба h= h_a+ h_f

• Диаметр вершин зубьев зубчатого колеса или шестерни d_a=d+2h_a=d+2m;

• Диаметр впадин зубчатого колеса или шестерни d_f=d-2h_f=d-2,5m.

• Отношение числа зубьев колеса к числу зубьев шестерни называют передаточным числом u. Учитывая, что передаточное отношение(отношение угловой скорости ведущего вала к угловой скорости ведомого вала) и делительный диаметр d=mz и =0,5 ₁d₁=0,5 ₂d₂, получаем u=z₂/z₁=d₂/d₁= ₁/ ₂=i.

• Межосевое расстояние a_w=0,5(d₁+d₂)=0,5mz =0,5mz₁(u+1). Где z = z₁+ z₂.

• Отношение длины зацепления g_a к окружному шагу p_b по основной окружности называется коэффициентом торцового перекрытия _а : _а= g_a/ p_b. Для непрерывной нормальной работы зубчатой передачи необходимо, чтобы длина зацепления была больше окружного шага р_b : g_a р_b и _а = g_a/ p_{b 1.} Если _{а 1}, то до выхода из зацепления одной пары зубьев к линии зацепления подходит другая пара зубьев- это и обеспечивает непрерывность зацепления и плавность хода передачи. При _а 1 передача нормально работать не будет,т.к. при выходе из зацепления одной пары зубьев другая пара не попадает на линию зацепления и непрерывность вращения зубчатых колес нарушается, т.е. в этом случае произойдет перерыв в зацеплении, относительные окружные скорости зубчатых колес изменятся и зацепление следующей пары будет сопровождаться ударом. При _а=1 передача может работать нормально только теоретически. Значение коэффициента перекрытия показывает, сколько пар зубьев в среднем одновременно находится в зацеплении.