2.5. Цепь переменного тока с последовательным соединением активного, индуктивного и ёмкостного сопротивлений.

При последовательном соединении активного, индуктивного и емкостного сопротивлений через все элементы цепи проходит один и тот же ток (рис. 2.10), мгновенное значение которого описывается уравнением

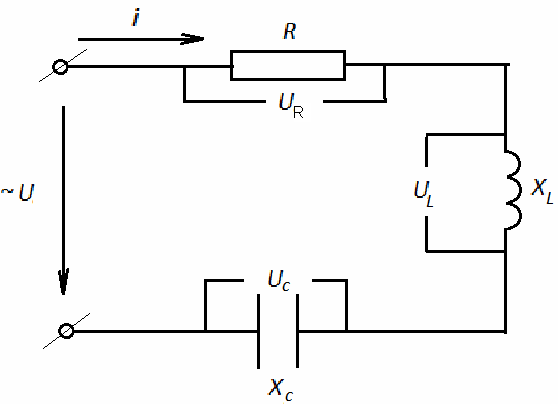
Рис. 2.10 Цепь переменного тока с последовательным соединением активного, индуктивного и ёмкостного сопротивлений.

Ток вызывает соответствующие падения напряжений:

- в активном сопротивлении , активное падение напряжения

– которое совпадает по фазе с током;

- в индуктивном сопротивлении, индуктивное падение напряжения – опережающее ток на угол 90°;

- в емкостном сопротивлении, емкостное падение напряжения – отстающее от тока на 90°.

Составим по второму закону Кирхгофа уравнение равновесия напряжений:

При сложении синусоидальных величин одинаковой частоты получается синусоидальная величина той же частоты с амплитудой равной геометрической сумме амплитуд складываемых величин:

Разделив все члены уравнения на получаем уравнение в действующих значениях напряжений:

На основании этого уравнения построим векторную диаграмму рассматриваемой цепи. При этом в качестве исходного или базисного вектора выбирается вектор тока, т.к. он одинаков для всех элементов цепи. По отношению к этому вектору откладываются вектора напряжений в соответствии с выбранным масштабом (рис 2.11).

Рис. 2.11 Векторная диаграмма цепи переменного тока с последовательным соединением R, X_L, X_C.

Диаграмма построена в предположении, что

Полученный треугольник ОАВ называют треугольником напряжений.

Алгебраическая сумма напряжений называется реактивным напряжением и обозначается через

(1)

Из треугольника ОАВ получим:

(2)

Откуда имеем

(3)

Уравнение (3) представляет собой закон Ома для цепи переменного тока с последовательным соединением активного, индуктивного и емкостного сопротивлений, где

- полное сопротивление цепи

Из треугольника ОАВ (рис. 2.11) можно определить значения активного и реактивного напряжений последовательной цепи переменного тока:

Если все стороны треугольника напряжений разделить на величину тока I получим треугольник сопротивлений.

Откуда

Если все стороны треугольника напряжений умножить на величину тока I , то получим треугольник мощностей.

Где S – полная мощность последовательной цепи [ВА].

– называется коэффициентом мощности цепи, потому что его величина показывает какая часть полной мощности цепи является активной.

2.6. Резонанс напряжений

В последовательной цепи переменного тока с активным, индуктивным и емкостным сопротивлениями, в зависимости от соотношений X_L и X_C, можно выделить три характерных режима ее работы при: X_L >X_C, X_L <X_C и X_L=X_C

Построим векторные диаграммы для всех трех случаев (рис. 2.12)

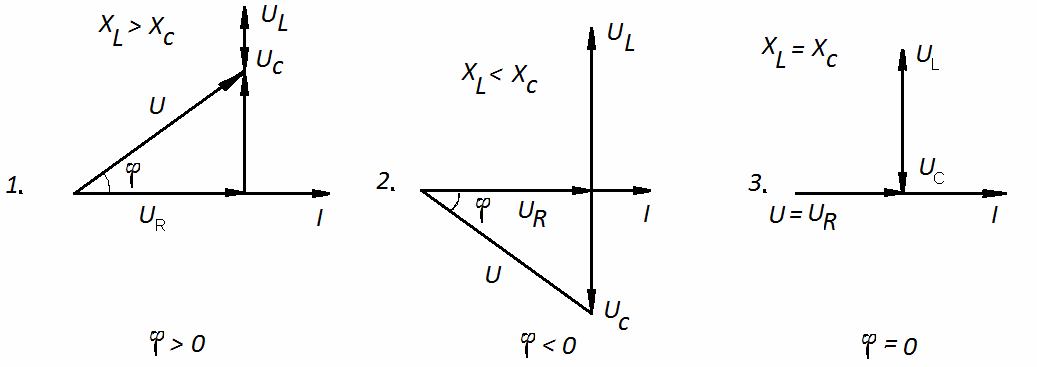
Рис. 2.12 Векторные диаграммы режимов работы последовательной цепи переменного тока.

Третья векторная диаграмма аналогична диаграмме цепи переменного тока с активным сопротивлением на величину тока с активным сопротивлением, в том смысле, что напряжение и ток совпадают друг с другом, угол сдвига фаз между ними . Отсутствие влияния реактивных сопротивлений на величину тока в цепи объясняется тем, что при равенстве между собой X_L и X_C, равные между собой и смещенные относительно друг от друга на 180° U_L и U_C взаимно компенсируются.

Величина тока в цепи при этом определяется активным сопротивлением и достигает максимального значения.

=I _max (4)

Такой режим работы последовательной цепи переменного тока, когда ток достигает наибольшего значения, при , называется резонансом напряжений. Условием достижения резонанса напряжений последовательной цепи является равенство:

Хотя, при резонансе напряжений, напряжения U_L и U_C не оказывают влияния на величину тока в цепи, эти напряжения существуют и могут значительно превышать напряжение, приложенное к зажимам цепи

Действительно

Отсюда видно, что при резонансе напряжений, напряжения на индуктивном или емкостном сопротивлениях во столько раз больше напряжения, приложенного к зажимам цепи, во столько раз индуктивное или емкостное сопротивление больше активного сопротивления цепи.

Резонанс напряжений можно вызвать двумя способами:

а) изменением емкости конденсаторной батареи

б) изменением частоты питающего тока

а) Если постепенно увеличивать емкостное сопротивление от нуля до некоторого конечного значения, то как видно из (3), ток начинает возрастать и достигает наибольшего значения тогда, когда X_С окажется равным X_L. Дальнейшее увеличение емкостного сопротивления приводит к снижению тока. Сказанное можно проиллюстрировать графиком (рис. 2.13).

Рис. 2.13 К определению резонанса напряжений.

б) Как видно из условия резонанса напряжений:

. , откуда

или φ _р , где φ_р– резонансная частота тока

Сказанное иллюстрируется графиком (рис. 2.14).

Рис. 2.14. К определению резонансной частоты питающего тока при резонансе напряжений.