1.7. Расчет сложных электрических цепей постоянного тока.

Универсальным методом расчета токов сложных цепей постоянного тока с несколькими источниками электрической энергии, является метод непосредственного применения I и II законов Кирхгофа.

Рассмотрим применение законов Кирхгофа к расчету сложной электрической цепи, схема которой представлена на рис. 1.10

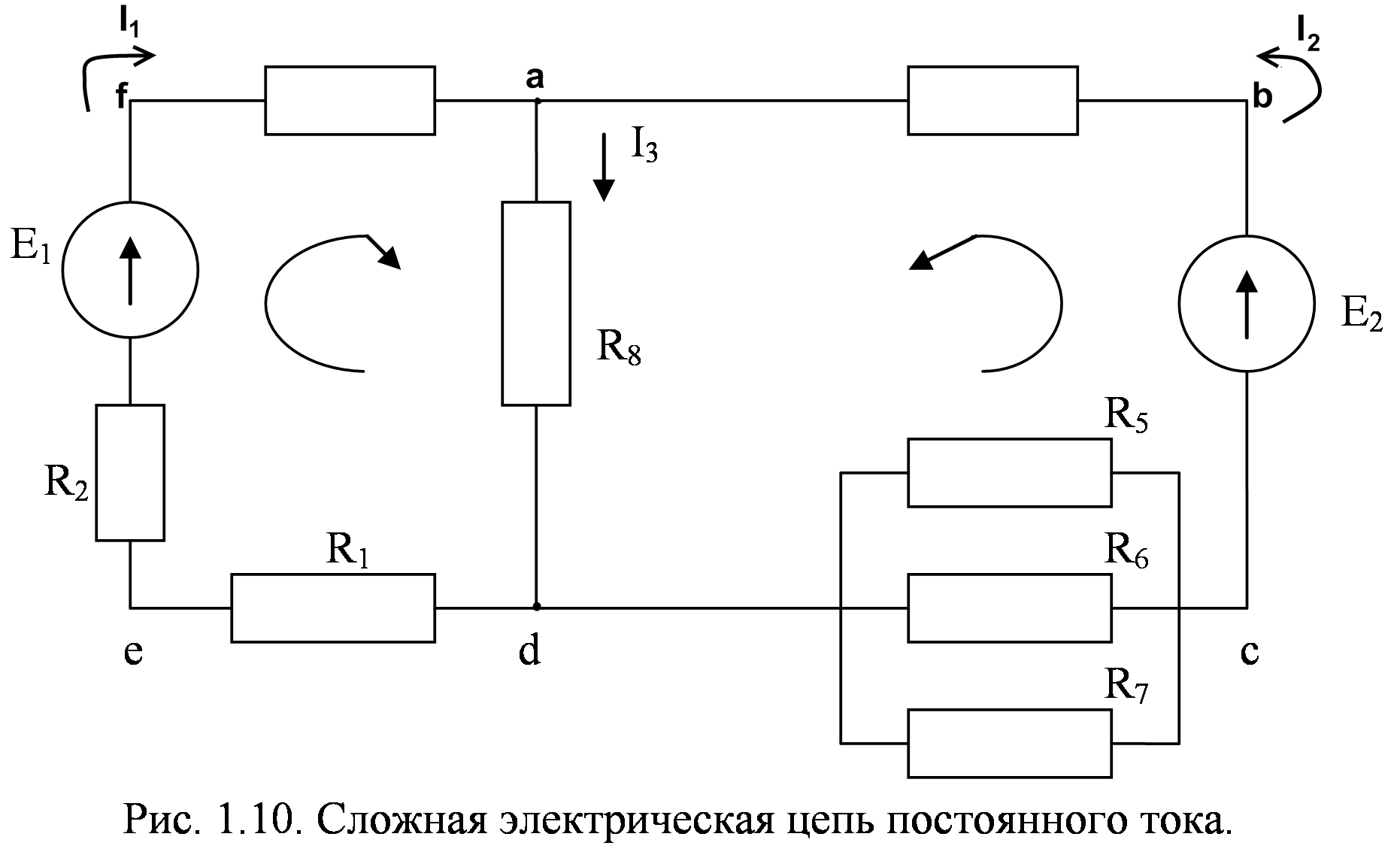
Приведем основные понятия сложной цепи. Несколько последовательно соединенных элементов цепи, по которым проходит один и тот же ток, образуют ветвь. В общем случае в ветви могут находиться как сопротивления, так и ЭДС.

Например, в рассматриваемой цепи имеется три ветви: abcd, ad, afed. Место соединения трех и более ветвей называют узловой точкой или узлом.

Несколько ветвей, образующих замкнутую электрическую цепь называют контуром. В данной схеме два контура: abcda, adefa.

К узловым точкам схемы применяется I закон Кирхгофа, согласно которому сумма токов, притекающих к узлу равна сумме токов уходящих от него, т.е. алгебраическая сумма токов в узле равна нулю. ∑I =0

К контурам применяется II закон Кирхгофа, согласно которому алгебраическая сумма ЭДС, действующих в контуре равна сумме падений напряжения на всех сопротивлениях контура.

∑E = ∑IR

По первому и второму законам Кирхгофа составляют столько уравнений, столько неизвестных токов в цепи. Количество токов в цепи определяется путем подсчета количества ее ветвей. По первому закону Кирхгофа составляют n-1 уравнений, где n – число узлов в цепи. Недостающие уравнения составляют по второму закону Кирхгофа.

Расчет сложной цепи про помощи уравнений Кирхгофа проводят по следующим правилам:

1. По возможности упрощают расчетную схему, заменяя параллельно соединенные сопротивления одним эквивалентным;

2. Для всех ЭДС, входящих в рассчитываемую цепь, устанавливают направления их действия;

3. Определяют количество ветвей в цепи и произвольно задают направления всех искомых токов

4. Определяют количество узлов в цепи и для всех узловых точек, кроме одной составляют уравнения по первому закону Кирхгофа. В рассматриваемой цепи после замены параллельно включенных сопротивлений R₅, R₆, и R₇ эквивалентным сопротивлением R₅₆₇ останутся две узловые точки a и d. Поэтому по первому закону Кирхгофа составляется одно уравнение для узловой точки a.

I₁ + I₂ = I₃ (11)

5. Выбирают произвольное направление обхода контуров по или против часовой стрелки и по второму закону Кирхгофа составляют недостающие уравнения.

В рассматриваемой цепи три ветви, следовательно, и три неизвестных тока. Для их определения необходимо составить три уравнения. Одно уже составили по первому закону Кирхгофа, значит, два других уравнения составляются по второму закону Кирхгофа, для контуров adef и abcd в соответствии с выбранными направлениями их обхода. При этом ЭДС и токи, совпадающие с направлением обхода контура, принимают со знаком плюс, а ЭДС и токи, противоположные этому направлению, со знаком минус. В результате получаем

E₁ = I₁ (R₁+R₂+R₃) + I₃R₈ (12)

E₂ = I₂ (R₅₆₇+R₄) + I₃R₈ (13)

где R₅₆₇ =

Совместно решая полученную систему уравнений (11), (12), (13) определяют неизвестные токи в ветвях. Если какие-то токи при расчете получаются со знаком минус, то это означает, что реальные токи имеют направления противоположные заданным в начале расчета.

Проверку решения задачи осуществляют путем расчета уравнения баланса мощностей: алгебраическая сумма мощностей развиваемых всеми источниками энергии равна алгебраической сумме мощностей всех потребителей. В общем виде уравнение баланса мощностей записывается как

∑EI=∑I²R.

Применительно к рассматриваемой цепи уравнение баланса мощностей принимает вид:

E₁I₁+E₂I₂ = I (R₁+R₂+R₃) + I (R₄+R₅₆₇) +I R₈

Е сли направление ЭДС совпадает с направлением тока в ветви, то их произведение включается в левую часть уравнения со знаком плюс, а если не совпадают, то со знаком минус, т.е. E I (+) и EI (-).

Если левая часть уравнения равна его правой части, значит задача решена правильно.