3.6. Мощность трехфазной системы при соединении треугольником.

Мощность трехфазной системы равна сумме мощностей ее отдельных фаз:

Р=Р_АВ+Р_ВС+Р_СА

Q=Q_AB+Q_BC+Q_CA

При симметричной нагрузке мощности отдельных фаз равны между собой, следовательно,

Р = 3Р_ф = 3 U_фI_Ф cosφ

Q= 3Q_ф = 3 U_фI_Ф sinφ

S = 3 U_фI_Ф

Учитывая, что при соединении треугольником U_л = U_ф и I_Л = получаем

Р = U_ЛI_Л cosφ

Q= U_ЛI_Л sinφ

S = U_ЛI_Л

Таким образом мощности трехфазной цепи при соединении «звездой» и «треугольником» рассчитываются по одинаковым формулам.

3.7. Измерения мощности потребляемой трехфазными электроприемниками.

Измерение активной мощности в трехфазной системе при симметричной нагрузке может быть осуществлено измерением мощности в одной любой фазе с последующим умножением полученного значения на три (рис. 3.10).

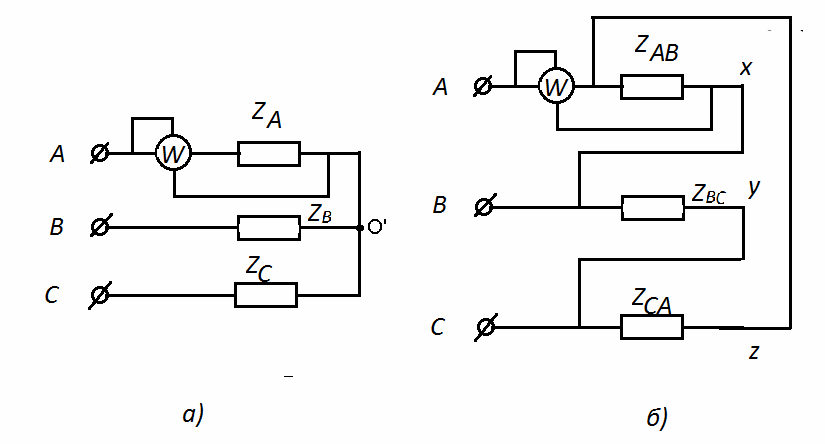
Рис. 3.10 (a,б). Схемы измерения активной мощности в симметричных трехфазных цепях: а) соединение звездой; б) соединение треугольником.

Активная мощность, потребляемая каждой схемой, определятся по формуле:

P=3W, где W – показания ваттметра.

В несимметричной четырехпроводной трехфазной системе, активная мощность определяется методом трех ваттметров (рис. 3.11)

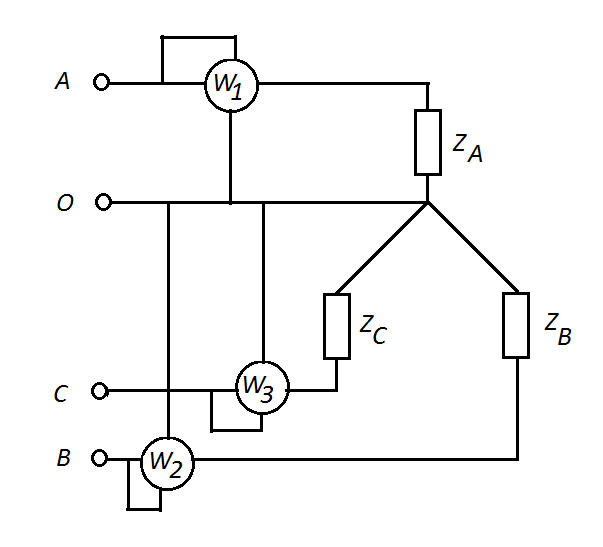
Рис. 3.11 Схема измерения мощности в четырехпроводных цепях трехфазного тока.

Активная мощность, потребляемая цепью, определяется как арифметическая сумма показаний всех ваттметров

P = W₁ + W₂ + W₃

В трехпроводных системах трехфазного тока при любой нагрузке для определения мощности широко применяют схему измерения мощности двумя ваттметрами.

Схема включения ваттметров показана на рис. 3.12.

На схеме токовые обмотки ваттметров включены в линейные провода А и В, а обмотки напряжений включены на линейные напряжения U_AC и U_BC.

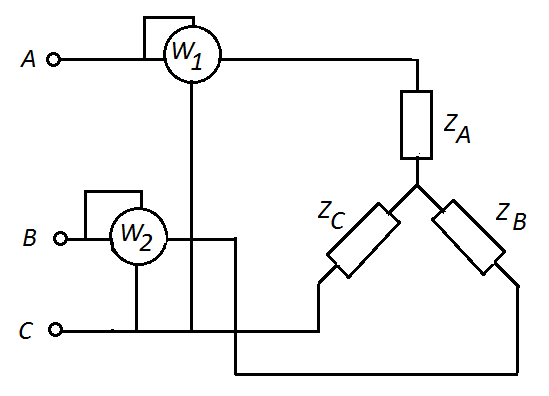
Рис.3.12 Схема измерения мощности в трехпроводных системах двумя ваттметрами

Поясним принцип работы схемы. Известно, что мгновенная мощность системы равна сумме мгновенных мощностей, потребляемых всеми фазами:

р=u_Ai_A+ u_Bi_B + u_Ci_C (1)

Так как сумма мгновенных значений токов в трехпроводной системе

i_A+i_B+i_C = 0, то

i_C = - (i_A+i_B) (2)

Подставляя (2) в (1) получим уравнение:

р = u_Ai_A+ u_Bi_B - u_C( i_A+i_B) = i_A(u_A-u_C) + i_B(u_B-u_C)= i_Au_AC+i_Bu_BC

П ри переходе от мгновенных значений токов и напряжений к их действующим значениям уравнение (2) принимает вид:

Р = I_AU_AC cos( I_AU_AC) + I_BU_BC cos (I_AU_BC) = W₁+W₂

При симметричной нагрузке линейные токи I_A, I_B и I_C равны между собой, также равны между собой и линейные напряжения U_AC и U_BC.

С помощью векторной диаграммы покажем, что действительно Р = W₁+W_2.

Построим векторную диаграмму токов и напряжений при симметричной нагрузке электроприемника, исходя из равенств:

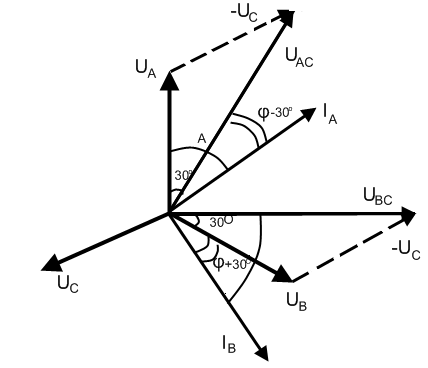
Рис. 3.13. Векторная диаграмма при соединении потребителей звездой.

Т аким образом, показания первого и второго ваттметров равны:

W ₁=I_AU_ACcos = I_ЛU_Л cos (φ-30^o)

W₂=I_ВU_ВСcos = I_ЛU_Л cos (φ+30^o).

W₁ + W₂ = I_ЛU_Л cos (φ-30^o) + I_ЛU_Л cos (φ+30^o) = I_ЛU_Л (cosφ cos30^о + sinφ sin30^o + cosφ cos30^{о -} sinφ sin30^o) = 2 I_ЛU_Л cosφ cos30^о = cosφ = P (см. разделы 3.4, 3.6).

По разности показаний ваттметров можно определить реактивную мощность трехфазной системы. Действительно

W₁-W₂ = I_ЛU_Лcos(φ-30^o) - I_ЛU_Лcos(φ+30^o) = I_ЛU_Л (cosφ cos30^о+ sinφsin30^o - cosφ cos30^о+ sinφ sin30^o) = 2 I_ЛU_Л sinφsin30^o) = I_ЛU_Лsinφ, (3)

Выше было получено выражение для определения реактивной мощности Q трехфазной цепи. Независимо от вида соединения фаз

Q= U_Л I_Л sinφ (4)

Сравнивая (3) и (4) получаем

Q= (W₁-W₂)

при φ = ±60 один из ваттметров будет показывать нулевое значение мощности. Вся мощность трехфазной системы, при этом, определяется по показаниям второго ваттметра.

при φ = >60 один из ваттметров покажет отрицательное значение мощности. Для снятия показаний ваттметров, в этом случае, необходимо изменить направление тока в токовой обмотке ваттметра и полученное показание взять в расчет со знаком минус.

48