3.3 Соединение звездой. Трехпроводная система трехфазного тока.

При симметричной нагрузке в четырехпроводной системе трехфазного тока, включенной по схеме звезда, ток в нейтральном проводе равен нулю, следовательно, в этом случае от нейтрального провода можно отказаться, и четырехпроводная система при этом превращается в трехпроводную систему трехфазного тока (рис. 3.6.)

Рис. 3.6 Трехпроводная система трехфазного тока при соединении звездой.

Векторная диаграмма, токов и напряжений в трехпроводной системе «звезда» при симметричной нагрузке представлена на рис. 3.7.

Рис. 3.7. Векторная диаграмма трехфазной системы «звезда» при симметричной нагрузке.

Электрические сети выполняются трехпроводными только для питания таких потребителей, которые обеспечивают симметричную нагрузку всех трех фаз (например, электрические двигатели).

Напряжения между линейными проводами остаются равными по величине (U_AB = U_BC = U_CA) и взаимно сдвинутыми по фазе на 120^о как при симметричной, так и при несимметричной нагрузке фаз. Фазные же напряжения в трехпроводной сети одинаковы по величине только в случае симметричной нагрузки фаз. При нарушении симметричности нагрузки напряжения между линейными проводами и нулевой точкой, т.е. фазные напряжения потребителей U_А, U_В и U_C будут неодинаковы. Поэтому соотношение U_Л= U_ф в трехпроводной сети справедливо только при симметричной нагрузке фаз.

3.4. Мощность трехфазной цепи при соединении звездой.

Активные и реактивные мощности в каждой из фаз трехфазной системы можно найти по следующим формулам:

Р_A=U_AI_A сosφ_A, Р_A=U_BI_B cosφ_B, Р_C=U_CI_C cosφ_C

Q_A=U_AI_A sinφ_A, Q_B=U_BI_B sinφ_B, Q_C=U_CI_C sinφ_C

Активная и реактивная мощности трехфазной системы равна сумме активных и реактивных мощностей фаз соответственно

Р=Р_А + Р_В + Р_С,

Q = Q_A + Q_B + Q_C

При симметричной нагрузке P_A = P_B = P_C = P_Ф; Q_A = Q_B = Q_C = Q_Ф;

φ_{А =} φ_{В =} φ_{С =} φ;

Тогда

P = 3P_ф = 3 U_фI_ф Cosφ,

Q = 3Q_ф = 3 U_фI_ф Sinφ,

S=3U_фI_ф.

Для линейных величин тока и напряжения, учитывая, что при соединении звездой I_Л = I_Ф и U_Л = U_ф, получим:

P = U_ЛI_Л Cosφ,

Q = U_ЛI_Л Sinφ,

S = U_ЛI_Л.

3.5. Соединение по схеме «треугольник.

Если конец первой фазы трехфазного генератора соединить с началом второй, конец второй фазы с началом третьей, конец третьей фазы с началом первой, то получится соединение треугольником. По такому принципу могут быть соединены и сопротивления нагрузки. Одноименные вершины фаз генератора и фаз нагрузки соединяются между собой линиями передач (рис. 3.8)

По сопротивлениям нагрузки проходят фазные токи I_AB, I_BC и I_AC, а по линейным проводам линейные I_A, I_B и I_C. Принятые положительные направления фазных и линейных токов обозначены стрелками. Напряжения, приложенные к сопротивлениям нагрузки Z_AB, Z_BC и Z_СА называются фазными напряжениями.

Таким образом, при соединении потребителей трехфазного тока треугольником фазные напряжения равны линейным.

U_ф= U_Л

Рис.3.8 Трехпроводная система трехфазного тока при соединении треугольником.

С оставим для узловых точек А, В, и С уравнения мгновенных значений токов:

А. i_A + i_CA = i_AB;

B. i_B + i_AB = i_BC;

С. i_C + i_BC = i_CA.

Откуда мгновенные значения линейных токов:

i_A = i_AB – i_CA

i_B=i_BC – i_AB (1)

i_C=i_CA-i_BC

В действующих значениях токов система (1) справедлива в векторной форме:

_A = _AB – _CA

_B= _BC – _AB (2)

_C= _CA- _BC

Из системы уравнений (2) следует:

1. Каждый линейный ток в трехфазной цепи при соединении треугольником равен геометрической разности двух прилегающих к узловой точке фазных токов;

2. При любых значениях фазных токов геометрическая сумма линейных токов равна нулю, как при симметричной, так и при несимметричной нагрузке.

На основании системы уравнений (2) построим векторную диаграмму фазных и линейных токов при соединении потребителей трехфазного тока треугольником (рис. 3.9) для симметричной нагрузки.

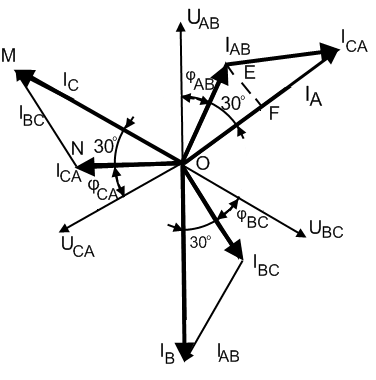
Рис. 3.9. Векторная диаграмма трехпроводной системы «треугольник» при симметричной нагрузке.

Из треугольника OEC определим, применив рассуждения, аналогичные рассмотренным для напряжений при соединении звездой, (см. раздел 3.2) получаем

I_Л= .

Таким образом, при симметричной нагрузке системы, соединенной в треугольник, линейные токи больше фазных в раз, а линейные напряжения равны фазным.