3.2. Соединения трехфазного тока.
А. Соединение звездой, четырехпроводная система.
Если объединить
между собой три конца обмоток генератора
х, у, z
и три вывода сопротивлений нагрузки
ZA,
ZB,
ZC
в общие точки О и
,
а свободные начала обмоток генератора
АВС и выводы сопротивлений нагрузки,
соединив соответственно между собой,
то получится соединение звездой.
Если общие точки О и также соединить между собой, то получится четырехпроводная трехфазная система переменного тока (рис. 3.4) называемая также соединение звездой с нулевым проводом. Обмотки генератора ОА, ОВ и ОС называются фазами генератора, а сопротивления ZA, ZB, ZC – фазами нагрузки.
Рис. 3.4. Четырехпроводная система трехфазного тока.
Точки О и O’ называются соответственно нулевой точкой генератора и нулевой точкой нагрузки, а провод ОO’ называется нулевым или нейтральным проводом.
Провода АА, ВВ и СС называются линейными проводами.
Напряжение между линейным и нулевым проводами называют фазным напряжением и обозначают через UA, UB и UC. Напряжение между двумя линейными проводами называют линейным напряжением и обозначают через UAB, UBC и UCA.
Как видно на рис. 3.4 к сопротивлениям нагрузки ZA, ZB и ZC подведены фазные напряжения. В трехфазных цепях переменного тока различают линейные Iл и фазные Iф токи. Линейными называют токи IА IВ и IС, проходящие по линейным проводам. Токи, проходящие по обмоткам генератора или по сопротивлениям нагрузки – называются фазными токами.
При соединении звездой каждая фаза генератора, линейный провод и фаза нагрузки, соединены между собой последовательно, и через них проходит один и тот же ток. Следовательно, при соединении звездой линейный ток равен фазному, т.е.
Iл = Iф
В трехфазных цепях при соединении звездой фазные токи вызываются только фазными напряжениями и между ними существуют соотношения, определяемые законом Ома:
IА
=
IВ
=
IС=
Сдвиг по фазе между фазным током и фазным напряжениям определяется по формулам:
Сos
φА=
;
Сos
φВ=
Сos
С=
Величину тока, протекающего по нулевому проводу, определяют как геометрическую сумму фазных токов:
В трехфазных цепях различают симметричные и несимметричные нагрузки. Нагрузка называется симметричной, если сопротивления и углы сдвига между током и напряжением всех фаз нагрузки одинаковы, т.е.
ZA = ZB = ZC
φA=φB=φC (1)
Если хотя бы одно из условий (1) не выполняется, нагрузка трехфазной системы называется несимметричной.
На рис. 3.4 стрелками указаны положительные направления фазных напряжений: UA, UB и UC.
Для определения мгновенных значений линейных напряжений составим систему уравнений:
uAB=uA + (-uB)
uBC=uB + (-uC) (2)
uCA=uC + (-uA)
В действующих значениях линейных напряжений система (2) будет справедлива в векторной форме
AB= A - B
BC= B - C (3)
CA= C - A
На основе уравнений (3.13) построим векторную диаграмму фазных и линейных напряжений (рис. 3.5)
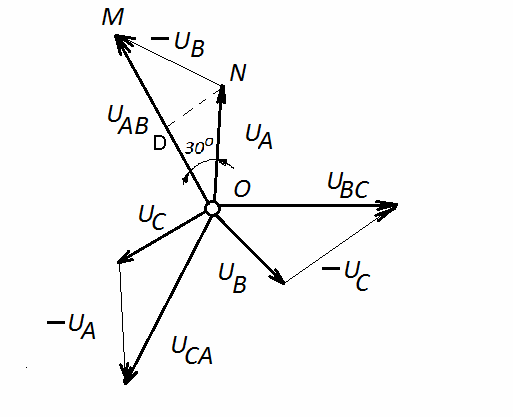
Рис. 3.5 Векторная диаграмма напряжений трехфазной цепи при соединении звездой с нулевым проводом.
ИЗ диаграммы (рис.3.5) видно, что все три линейных напряжения равны между собой и смещены друг от друга на 120о.
Из равнобедренного треугольника OMN находим:
OM = 2OD
OD
=
Т.к. Uл
=UAB=OM,
U
ф=
UA=
ON,
а ND
= ONsin30o=
то окончательно получаем
Uл=2
(4)
Таким образом, при
соединении трехфазного тока звездой с
нейтральным проводом линейное напряжение
в
раз
больше фазного напряжения.
Четырехпроводная система трехфазного тока звездой применяется для питания несимметричной нагрузки, например, осветительной, где симметричность нагрузки нарушается при отключении ламп накаливания, включаемых в одну из фаз.
Анализ работы четырехпроводной системы трехфазного тока, включенной по схеме звезда, позволяет сделать следующие выводы:
1. Линейные токи равны фазным.
2. Все линейные напряжения равны между собой и смещены друг от друга на 120о.
3. Все фазные напряжения равны между собой и в раз меньше линейных напряжений, независимо от симметричности нагрузки.
4. При несимметричной нагрузке ток в нулевом проводе определяется как геометрическая сумма фазных токов ( ), при симметричной нагрузке ток в нулевом проводе равен нулю ( =0).