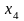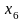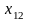- •Вопрос 26.
- •Центральной симметрией относительно начала координат,
- •Двуполостный гиперболоид.
- •Центральной симметрией относительно начала координат,
- •Цилиндрические поверхности
- •Вопрос 27. Переменные и постоянные величины.
- •Функция. Способы ее задания
- •Вопрос 28. Предел функции. Свойства пределов
- •Свойства пределов
- •Замечательные пределы
- •Вопрос 29. Непрерывность функции
- •Свойства непрерывных функций
Вопрос 28. Предел функции. Свойства пределов
Если при вычислении
предела последовательности всегда
 ,
то, вычисляя предел функции
,
то, вычисляя предел функции
 ,
следует оговаривать, к чему стремится
ее аргумент. Рассмотрим, в чем различие
между пределами последовательности
,
следует оговаривать, к чему стремится
ее аргумент. Рассмотрим, в чем различие
между пределами последовательности
 и функции
и функции
 .
Если в последовательности
возрастает, принимая только значения
из множества натуральных чисел, то
может возрастать, принимая любые
вещественные значения. Пределы
последовательности и функции в этом
случае равны нулю. В то же время имеет
смысл рассмотреть предел
.
Если в последовательности
возрастает, принимая только значения
из множества натуральных чисел, то
может возрастать, принимая любые
вещественные значения. Пределы
последовательности и функции в этом
случае равны нулю. В то же время имеет
смысл рассмотреть предел
 .
Стоящая под знаком предела функция
увеличивается с приближением ее аргумента
к нулю, оставаясь положительной, причем,
при
сколь угодно близких к нулю, ее значение
становится все большим и большим. Ясно,
что
.
Стоящая под знаком предела функция
увеличивается с приближением ее аргумента
к нулю, оставаясь положительной, причем,
при
сколь угодно близких к нулю, ее значение
становится все большим и большим. Ясно,
что
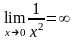 .
Поскольку при
.
Поскольку при
 рассматриваемая функция не существует,
этот ее предел дает важнейшую информацию
– показывает поведение функции в
окрестности предельной точки. При
подходе к этой точке она уходит в
бесконечность. Можно рассматривать
предел этой функции и при
,
стремящемуся к любому другому значению,
например
рассматриваемая функция не существует,
этот ее предел дает важнейшую информацию
– показывает поведение функции в
окрестности предельной точки. При
подходе к этой точке она уходит в
бесконечность. Можно рассматривать
предел этой функции и при
,
стремящемуся к любому другому значению,
например
 ,
но этот предел вычислять не имеет
смысла, поскольку известно значение
функции, как в самой точке, так и в ее
окрестности.
,
но этот предел вычислять не имеет
смысла, поскольку известно значение
функции, как в самой точке, так и в ее
окрестности.
Основной вывод. Если предел последовательности вычисляется всегда при , то предел функции зависит от того, к какому значению стремится ее аргумент.
Определение 1.
Число
 называется пределом функции
при
называется пределом функции
при
 ,
если для любой последовательности
значений аргумента
,
если для любой последовательности
значений аргумента
 ,
стремящейся к
,
стремящейся к
 ,
соответствующая ей функциональная
последовательность
,
соответствующая ей функциональная
последовательность
 сходится к
.
сходится к
.
Определение 1а.
Число
называется пределом функции
при
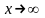 ,
если для любой последовательности
значений аргумента
,
если для любой последовательности
значений аргумента
 соответствующая ей функциональная
последовательность
соответствующая ей функциональная
последовательность
 сходится к
.
сходится к
.
Обозначение
предела функции
 .
На рисунке изображены
три последовательности
,
стремящиеся к a.
.
На рисунке изображены
три последовательности
,
стремящиеся к a.
![]()

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В первой все ее члены больше a, и мы подходим к точке a справа, во второй все элементы меньше предельного значения аргумента, подходим к точке a слева, в третьей элементы последовательности расположены как слева, так и справа от предельного значения a. Соответствующие им функциональные последовательности во всех трех случаях стремятся к b. Если для любой другой последовательности , стремящиеся к a, последовательность также стремится к b, то предел функции равен этому числу, что видно из рисунка.
Определение 2.
Число
называется пределом функции
при
,
если
 .
.
С ловесная
формулировка приведенной фразы такова:
число
называется пределом функции
при
,
если для любого положительного
ловесная
формулировка приведенной фразы такова:
число
называется пределом функции
при
,
если для любого положительного
 существует такое
существует такое
 ,
что при выполнении неравенства
,
что при выполнении неравенства
 выполняется неравенство
выполняется неравенство
 .
.
О пределение
2а. Число
называется пределом функции
при
,
если
пределение
2а. Число
называется пределом функции
при
,
если

Доказана эквивалентность этих двух определений, то есть из 1 следует 2, и наоборот.
Пример.
Покажем, что

Из определения 2 предела функции следует, что
если
 ,
то
,
то
З начит,
если для любого значения
начит,
если для любого значения
![]() мы
найдем соответствующие
мы
найдем соответствующие
![]() ,
то мы докажем, что
,
то мы докажем, что
Возьмем круг радиуса 1, обозначим радиальную меру угла MOB через x. Рассмотрим случай x > 0. Очевидно, что

Рассмотрим
треугольник
 и сектор
и сектор


 ,
т.е.
,
т.е.
 .
.
Очевидно,
что при x
< 0 будет
 .
.
Так
как
 ,
то
,
то
 - мы нашли. Значит, из определения предела
функции следует, что
- мы нашли. Значит, из определения предела
функции следует, что
К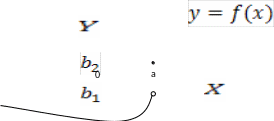 ак
мы уже говорили, в определении предела
функции
считается, что x
стремится к a
любым способом. Бывают случаи, когда
способ приближения аргумента
x
к a
существенно влияет на значение предела
функции, поэтому вводятся понятия
односторонних пределов.
ак
мы уже говорили, в определении предела
функции
считается, что x
стремится к a
любым способом. Бывают случаи, когда
способ приближения аргумента
x
к a
существенно влияет на значение предела
функции, поэтому вводятся понятия
односторонних пределов.
Определение 3.
Число
 называется левым пределом функции
при
(пределом слева),
если
называется левым пределом функции
при
(пределом слева),
если
 .
.
Обозначение
 .
.
Определение 4.
Число
 называется правым пределом функции
при
(пределом справа),
если
называется правым пределом функции
при
(пределом справа),
если
 .
.
Обозначение
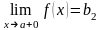 .
.
Очевидно, что
 если
если
 и
,
причем
и
,
причем
 .
.
Пример.
 Вычислим
Вычислим
 .
Поскольку
.
Поскольку
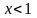 ,
показатель степени отрицательный,
следовательно,
,
показатель степени отрицательный,
следовательно,
 .
Теперь показатель степени положительный
и при
.
Теперь показатель степени положительный
и при
 стремится к
стремится к
 ,
ясно, что левый предел этой функции при
равен нулю. В то же время правый предел
,
ясно, что левый предел этой функции при
равен нулю. В то же время правый предел
 ,
так как показатель степени положителен
и стремится к
.
,
так как показатель степени положителен
и стремится к
.
Очевидно,
 не существует, так как при подходе к
предельному значению аргумента слева
и справа получаем разные значения, и
определение 1 не выполняется.
не существует, так как при подходе к
предельному значению аргумента слева
и справа получаем разные значения, и
определение 1 не выполняется.