Геометрическая интерпретация

Геометрически это означает замену графика функции f прямой, проходящей через точки (x₀,f(x₀)) и (x₁,f(x₁)).

График: пример линейной интерполяции

Уравнение такой прямой имеет вид:

отсюда для

Это и есть формула линейной интерполяции, при этом

где R₁(x) — погрешность формулы:

Справедлива оценка

11. Интерполяция полиномом и сплайны

Интерполяция полиномом

+)матрица сист всегда невырождена (определ <>0); гладкость ф-ции

-) неустойчивость метода

Метод Лагранжа +) позволяет не решать с-му у-ний; -)неустойчивость

Сплайны +) нет проблемы неустойчивости (осцеляции отсутствуют, т.к. маленький порядок); функция гладкая; не нужно больших массивов; -) немного больше вычислений

На практике вместо глобальной интерполяции чаще используют кусочно-полиномиальную интерполяцию: исходный отрезок разбивается на части и на каждом отрезке малой длины исходная функция заменяется многочленом невысокой степени. Система MatLab предоставляет возможность аппроксимации двумя важными классами функций: кусочно-линейной (или сплайнами первой степени) и сплайнами более высоких степеней.

Пусть - разбиение отрезка [a,b]. , - заданные значения. Функцию назовем полиномиальным сплайном степени дефекта с узлами , если

1. на ;

2. .

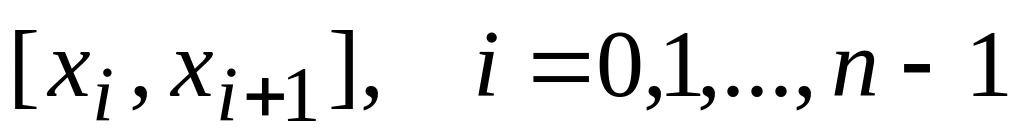Узлы называют узлами сплайна, -я производная разрывна.

Таким образом, сплайн можно представить в виде функции:

Где каждая функция является полиномом порядка m.

Линейная сплайн интерполяция

Сплайном первой степени называется :непрерывная на отрезке [a,b], линейная на каждом частичном промежутке функция. Это простейшая форма сплайна и она эквивалентна линейной интерполяции. Результирующий сплайн называется также полигон. График линейного интерполяционного сплайна - это ломаная, проходящая через заданные точки.

Убедитесь самостоятельно, что сплайн является интерполяционным.

Остаточный член : .

Оценка остаточного члена зависит от дифференцируемых свойств функции .

Пусть . Обозначим - колебание функции на отрезке . Тогда .

С улучшением гладкости функции оценка погрешности ее интерполяции линейными сплайнами также улучшается. А именно, если , то , где .

Для можно получить оценку .

Дальнейшее увеличение гладкости функции не дает повышения порядка аппроксимации. Происходит насыщение алгоритма.

Сходимость. Пусть на задана последовательность сеток , , которая удовлетворяют условию при . Для строится интерполяционный сплайн . Интерполяционный процесс сходится, если при для любой функции из некоторого класса. Отсюда вытекает возможность интерполяции с наперед заданной точностью:

Преимущество по сравнению с интерполяционными многочленами: из оценки погрешности следует сходимость.

Пусть . По доказанной теореме .

По определению при , поэтому процесс интерполяции линейными сплайнами сходится на множестве непрерывных функций по произвольной последовательности сеток . Если , то . Сходимость порядка .