1 Уравнения 2-го порядка с частными производными. Классификация. Приведение к каноническому виду.

Уравнения 2-го порядка с частными производными имеют вид

F(x,y,U,U_x,U_y,U_xx,U_xy,U_yy)=0

Уравнение называется линейным относительно производных, если оно имеет вид:

a₁₁U_xx+2a₁₂U_xy+a₂₂U_yy+f(x,y,U,U_x,U_y)=0 , где a₁₁,a₁₂,a₂₂ – функции от x и y.

a₁₁U_xx+2a₁₂U_xy+a₂₂U_yy+b₁U_x+b₂U_y+cU+φ(x,y)=0 - линейное уравнение.

Если a_ij≠ a_ij(x.y), то уравнение называется уравнением с постоянными коэффициентами.

Канонический вид – вид при котором остаются только смешанные(???) производные. В зависимости от знака выражения a₁₂^2­-a₁₁a₂₂ имеют место следующие канонические формы:

D>0 (гиперболический вид) U_αα-U_ββ=4Ф U_ξη=Ф

D<0 (эллиптический вид) U_αα+U_ββ=4Ф

D=0 (параболический вид) U_αα=4Ф

2.Основные физические задачи, приводящие к уравнениям гиперболического типа. Волновое уравнение. Уравнение колебаний струны.

К уравнениям гиперболического типа приводят задачи, состоящие в описании распространения упругих волн (звуковых) в однородной (непрерывной) среде, состоящие в нахождении характеристик движения жидкости, задач гидродинамики и акустики и многое другое.

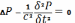волновое уравнение в пространстве для упругих (акустических) волн.

Если взять уравнение не в пространстве, а по оси X то получится уравнение, описывающие распространение волн в струне.

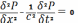U_tt=a²U_xx

3. Постановка краевых задач. Предельные случаи.

В случае обыкновенного дифференциального уравнения 2-го порядка решение может быть определено начальными условиями.

Рассмотрим простейшую задачу о поперечных колебаниях струны.

U(x,t) – отклонение струны от оси X

Тогда начальные условия имеют вид:

U(x,0)=φ(x) – отклонение струны в нулевой отрезок времени

U_t(x,0) – скорость точек струны в начальный момент времени.

Встречаются и другие формы дополнительных условий. Различают граничные условия 1.2и3 рода в зависимости от физической постановки задачи.

1. U(0,t)=α(t)

U(l,t)=β(t)

2. U_x(0,t)=µ(t)

U_x(l,t)=ν(t)

3. Все остальные

Уравнение +начальные условия + граничные = краевая задача.

Допустим нас интересуют колебания струны вблизи левого конца. Вблизи правого конца колебания малы и мы их не учитываем. Тогда одно из указанных условий уходит и мы получаем полубесконечную струну (0≤x<∞). Если нас интересует и 2е граничные условия, то получаем бесконечную струну(-∞<x<+∞). Мы можем пренебречь и начальными условиями, если система стационарна, т.е. не зависит от того, как была возбуждена система.

4 Бесконечная струна. Метод распространяющихся волн. Формула Даламбера.

Решим задачу для бесконечной струны

U_tt=a²U_xx

-∞<x<+∞ t≥0

U(x,0)=φ(x)

U_t(x,0)=ψ(x)

Общее решение задачи о колебании струны представляет собой сумму двух бегущих волн, распространяющихся влево и вправо соответственно

U(x,t)=f₁(x+at)+f₂(x-at)

Удовлетворив начальные условия мы найдем сами функции

Самостоятельно получим

U(x,0)=f₁(x)+f₂(x)=φ(x)

U_t(x,0)= af₁^/(x)+af₂^/(x)=ψ(x)

Интегрируем 2-е равенство

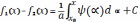
Из него и из первого находим f₁(x) f₂(x) :

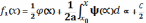
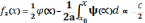
подставим в начало и получим:

- формула Даламбера

Таким образом волна разбивается на 2 волны.

5.Метод разделения переменных для уравнений гиперболического типа

Изучение метода приведено для задачи о колебании струны

U_tt=a²U_xx

U(0,t)=0 U(l,t)=0

U(x,0)=φ (x) U_t(x,0)=ψ (x)

Уравнение линейно и однородно, поэтому сумма частных решений также является решением этого уравнения. Имея достаточно большое число частных решений можно попытаться при помощи суммирования их с несколькими коэффициентами найти искомое решение.

Попытаемся найти частное решение уравнения в виде произведения 2х функций одно их которых зависит от x а другое от t.

U(x,t)=X(x)T(t)

Это равенство должно удовлетворятся тождественно.

Граничные условия дают Х(0)=X(l)=0

Задача состоит в исключении нетривиального решения

X⁽²⁾+λX=0

Такие значения параметра λ называются собственными значениями, а соответствующие нетривиальные решения собственными функциями