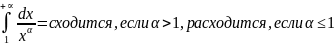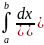- •Теорема о связи первообразной и функции. Понятие неопределенного интеграла
- •Свойства неопределенного интеграла. Интегрирование по частям. Круговой интеграл
- •1. Линейность:
- •2. Инвариантность формы интеграла:
- •3. Интегрирование по частям:
- •Интегрирование рациональных функций (1 теорема Остроградского).
- •Интегрирование иррациональных функций (подстановка Эйлера)
- •Интегрирование тригонометрических функций (универсальная тригонометрическая подстановка).
- •Вычисление площади криволинейной трапеции.
- •7) Замена переменной в определенном интеграле.
- •7)Понятие определенного интеграла
- •10. Вычисление длины дуги графика функции
- •11) Вычисление объема тела вращения
- •12) Несобственные интегралы, теорема сравнения
- •13. Теорема Коши, формулировка для дифференциального уравнения первого порядка.
- •14)Однородные дифференциальные уравнения первого порядка.
- •Дифференциальные уравнения с разделяющимися переменными
- •Дифференциальные уравнения в полных дифференциалах
- •Неполные дифференциальные уравнения, допускающие понижения порядка
- •Ду, не зависящие явно от у
- •2)Ду, не зависящие явно от х
- •Линейные дифференциальные уравнения с постоянными коэффициентами. Характеристическое уравнение
- •Линейная независимость решений ду. Определитель Вронского
- •Структура общего решения неоднородного линейного ду
- •21)Метод вариации произвольных постоянных
- •22) Линейные ду с квазимногочленом в правой части
- •23) Преобразования Лапласа. Изображения тождественной, единичной и показательной функции
- •24) Теорема линейности, подобия. Теорема затухания-смещения
- •25) Теорема о дифференцировании оригинала
- •26)Теорема о Дифференцировании изображения. Изображение свертки
11) Вычисление объема тела вращения
Пусть
тело Т находится между двумя плоскостями
х=а и х=b,
тогда его объем
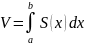 ,
где S(x)
площадь сечения плоскостью х=с,
перпендикулярной оси Ох и проходящей
через точку с, принадлежащую [a;b]
на этой оси.
,
где S(x)
площадь сечения плоскостью х=с,
перпендикулярной оси Ох и проходящей
через точку с, принадлежащую [a;b]
на этой оси.
Объем
тела вращения.
Объем тела, полученного, при вращении
вокруг оси Ох криволинейной трапеции,
ограниченной кривыми y=y(x),
x=a,x=b,y=0
находится по формуле
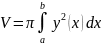 .
.
Объем
тела, полученного, при вращении вокруг
оси Оy
криволинейной трапеции, ограниченной
кривыми x=x(y),
y=c,y=d,x=0
находится по формуле
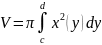 .
.
12) Несобственные интегралы, теорема сравнения
Если существует конечный
предел
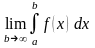 ,
то этот предел называется несобственным
интегралом с бесконечным пределом от
функции
,
то этот предел называется несобственным
интегралом с бесконечным пределом от
функции
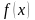 и обозначается
и обозначается
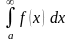 .
.
Итак, по определению
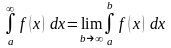 .
В этом и заключается метод вычисления
таких интегралов. Очевидно, что поскольку
данное вычисление связано с нахождением
предела, то ответ может существовать
или нет.
.
В этом и заключается метод вычисления
таких интегралов. Очевидно, что поскольку
данное вычисление связано с нахождением
предела, то ответ может существовать
или нет.
Определение 2. Если в несобственном интеграле предел существует, то интеграл называется сходящимся, если предел не существует или равен бесконечности, то интеграл называется расходящимся.
Очевидно, с геометрической
точки зрения несобственный интеграл с
бесконечными пределами равен площади
неограниченной области, лежащей между
осью
 ,
кривой
,
кривой
 и прямой
и прямой
 .
.
Аналогичным образом определяются несобственные интегралы и для других бесконечных интервалов:
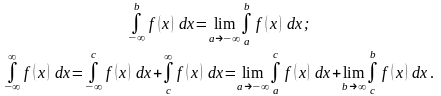
Следует подчеркнуть, что
интеграл
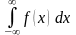 существует только тогда, когда существует
каждый из интегралов
существует только тогда, когда существует
каждый из интегралов
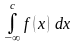 и
и
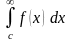 .
.
Из сказанного выше следует, что несобственный интеграл это не предел интегральной суммы, а предел определенного интеграла с переменным верхним пределом интегрирования.
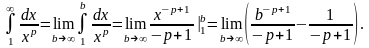
Если
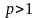 ,
то
,
то
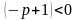 ,
поэтому
,
поэтому
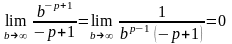 .
Следовательно, в этом случае
.
Следовательно, в этом случае
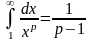 .
.
Если
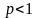 ,
то
,
то
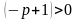 ,
поэтому
,
поэтому
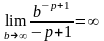 и
и
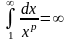 .
Аналогично, если
.
Аналогично, если
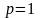 ,
то
,
то
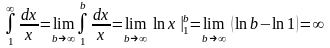 .
.
Таким образом,
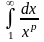 сходится, если
и расходится, если
сходится, если
и расходится, если
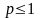 .
.
Если существует конечный
предел
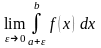 ,
то этот предел называется несобственным
интегралом от разрывной функции
и обозначается
,
то этот предел называется несобственным
интегралом от разрывной функции
и обозначается
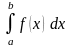 .
.
Следовательно, вычисление несобственного интеграла от разрывной функции связано с нахождением предела:
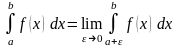 .
если этот предел существует, то интеграл
называется сходящимся, если не существует
или равен бесконечности, то – расходящимся.
.
если этот предел существует, то интеграл
называется сходящимся, если не существует
или равен бесконечности, то – расходящимся.
С геометрической точки зрения несобственный интеграл от разрывной функции равен площади криволинейной трапеции, у которой в какой-то точке высота равна бесконечности.
Если функция
терпит разрыв в точке
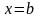 ,
то
,
то
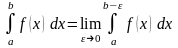 .
.
Если же разрыв происходит
в точке
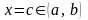 ,
то есть внутри
,
то есть внутри
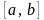 ,
то в этом случае
,
то в этом случае
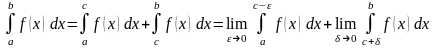 .
.
В последнем случае несобственный интеграл существует (или сходится), если сходятся оба интеграла.
Так же как и несобственный
интеграл с бесконечными пределами,
данный интеграл тоже не является пределом
 -ой
интегральной суммы, а пределом
определенного интеграла.
-ой
интегральной суммы, а пределом
определенного интеграла.
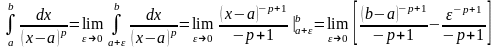
Если в этом интеграле
,
то
и поэтому
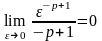 .
Следовательно, в этом случае
.
Следовательно, в этом случае
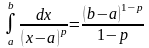 .
.
Если
,
то
.
В этом случае
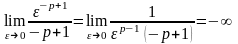 и интеграл
и интеграл
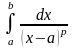 расходится. Аналогичный результат
получается и в том случае, когда
.
Действительно,
расходится. Аналогичный результат
получается и в том случае, когда
.
Действительно,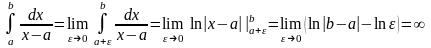 .
.
Таким образом, рассмотренный
интеграл расходится при
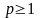 и сходится при
.
и сходится при
.
Теоремы о сходимости:
Теорема 1. Пусть функции
и
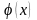 непрерывны на промежутке
непрерывны на промежутке
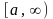 и удовлетворяют неравенствам
и удовлетворяют неравенствам
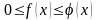 .
Тогда,
.
Тогда,
1) если интеграл
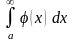 сходится, то сходится и интеграл
;
сходится, то сходится и интеграл
;
2) если интеграл расходится, то расходится и интеграл .
Теорема 2. Пусть
функции
и
непрерывны на промежутке
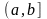 ,
удовлетворяют неравенствам
и в точке
одновременно терпят разрыв второго
рода. Тогда,
,
удовлетворяют неравенствам
и в точке
одновременно терпят разрыв второго
рода. Тогда,
1) если
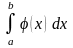 сходится, то
сходится также;
сходится, то
сходится также;
2) если расходится, то расходится и .
Теорема 3. Если
на промежутке
функция
меняет свой знак, то если
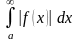 сходится, то сходится и
,
при этом второй интеграл называется
абсолютно сходящимся.
сходится, то сходится и
,
при этом второй интеграл называется
абсолютно сходящимся.
Теорема 4. Если
положительные функции
и
непрерывны на промежутке
и при этом
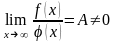 ,
то оба несобственных интеграла
и
ведут себя одинаково.
,
то оба несобственных интеграла
и
ведут себя одинаково.