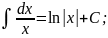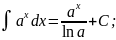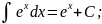Теорема о связи первообразной и функции. Понятие неопределенного интеграла …….2
Свойства неопределенного интеграла. Интегрирование по частям. Круговой интеграл…….3
Интегрирование рациональных функций (1 теорема Остроградского) …….…….4
Интегрирование иррациональных функций (подстановка Эйлера) …….…….5
Интегрирование тригонометрических функций (универсальная тригонометрическая подстановка)5
Вычисление площади криволинейной трапеции…….…….…….6
Понятие определенного интеграла. Теорема о существовании, формулировка…….6
Замена переменных интегрирования по частям в определенном интеграле…….7
Вычисление площади криволинейного сектора в полярных координатах…….8
Вычисление длины дуги графика функции…….…….…….8
Вычисление объема тела вращения…….…….8
Несобственные интегралы, теорема сравнения…….…….8.9
Теорема Коши, формулировка для дифференциального уравнения первого порядка…….12
Однородные дифференциальные уравнения первого порядка…….12.13
Дифференциальные уравнения с разделяющимися переменными…….13
Дифференциальные уравнения в полных дифференциалах…….…….14
Неполные дифференциальные уравнения, допускающие понижения порядка…….14
Линейные дифференциальные уравнения с постоянными коэффициентами. Характеристическое уравнение…….…….…….15
Линейная независимость решений ДУ. Определитель Вронского…….…….16
Структура общего решения неоднородного линейного ДУ…….…….16
Метод вариации постоянных для нахождения частного решения неоднородного линейного ДУ…….…….…….…….…….…….…….…….…….17
Линейные ДУ с квазимногочленом в правой части…….…….17
Преобразования Лапласа. Изображения тождественной, единичной и показательной функции…….…….…….…….…….…….…….…….…….…….19
Теорема линейности, подобия. Теорема затухания смещения…….20
Теорема о дифференцировании оригинала…….20
Теорема о дифференцировании изображений. Изображение свертки…….21
Теорема о связи первообразной и функции. Понятие неопределенного интеграла
Первообразной функции f(x) на некотором (конечном или бесконечном) интервале называется дифференцируемая функция F(x), производная которой равна f(x) во всех точках интервала, т.е. F’(x)=f(x).
Пусть F(x) – первообразная для f(x). Если С – постоянная, то функция F(x)+C также является первообразной для f(x). Наоборот, любая первообразная функции f(x) может быть представлена в виде F(x)+C, где С – некоторая постоянная. Таким образом, множество всех первообразных функции f(x) – это множество всех первообразных функций {F(x)+C}, т.е. для описания всех первообразных функции f(x) надо найти одну из них F(x), а затем прибавлять к ней произвольные постоянные.
Неопределённым интегралом
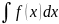функции f(x) называется множество всех
её первообразных. Следовательно,
(1), где F(x) – одна из первообразных,
а С – произвольная постоянная.
Для проверки формулы (1) достаточно найти производную функции F(x) и убедиться в том, что она равно подынтегральной функции f(x).
Отыскание неопределённого интеграла называется интегрированием функции. Будет доказано, что любая непрерывная функция имеет первообразную. Однако интеграл элементарной функции может не быть элементарной функцией (такие интегралы называются «неберущимися»).
Непосредственное интегрирование – это
интегрирование с помощью выполнения
алгебраических преобразований,
использования свойства линейности
неопределённого интеграла
и таблицы интегралов.
Таблица интегралов:
Интеграл 10 из этой таблицы принято называть высоким логарифмом, а интеграл 12 – длинным логарифмом.
Свойства неопределенного интеграла. Интегрирование по частям. Круговой интеграл
0.
,
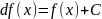1. Линейность:
2. Инвариантность формы интеграла:
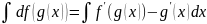
- способ интегрирования с помощью
подстановки.
Если
-
непрерывно дифференцируемая функция,
то
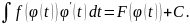(1)
Проверка формулы (1) следует из правила
дифференцирования сложной функции.
Формально формула (1) получается из
формулы
подстановкой везде вместо х функции
.
Метод замены переменной основан на
формуле (1) и состоит в следующем. Пусть
требуется найти
,
то есть найти первообразную F(x). Пусть
мы нашли такую функцию
,
что интеграл
мы можем вычислить. Тогда функция
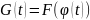получается из функции F(x)
заменой переменной
.
Поэтому для того, чтобы найти F(x) по
функции G(t), нужно в G(t) сделать обратную
замену переменной
.
Итак, метод замены переменной при вычислении состоит в следующем:
1) ищем замену , упрощающую интеграл;
2) вычисляем ;
3) делаем обратную замену
:
.
Как найти функцию , в общем случае неизвестно (и, кстати, не всегда возможно). В этом и состоит искусство вычисления интегралов. Для некоторых типов интегралов подстановки известны.
Замечание. Методы введения под знак дифференциала и замены переменной являются «двойственными» друг другу. Многие интегралы можно вычислять любым из них.
3. Интегрирование по частям:
,
,
,
(*),
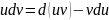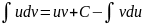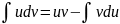где u=u(x) и v=v(x) – дифференцируемые функции.
Формула (*) позволяет свести вычисление
интеграла
к вычислению интеграла
,
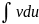который может оказаться проще. Для
применения формулы (*) к вычислению
интеграла
мы разбиваем подынтегральное выражение
на две части
и
.
Затем находим
и применяем формулу (*). Промежуточные
вычисления можно оформлять в фигурных
скобках, не прерывая вычисления интеграла.
Круговой интеграл. В интегральном исчислении, эллиптический интеграл появился в связи с задачей вычисления длины дуги эллипса и был впервые исследован Джулио Фаньяно и Леонардом Эйлером.
В современном представлении, эллиптический интеграл — это некоторая функция f, которая может быть представлена в следующем виде:
,
где R — рациональная функция двух аргументов, P — квадратный корень из многочлена 3 или 4 степени с несовпадающими корнями, c — константа.
В общем случае, эллиптический интеграл не может быть выражен в элементарных функциях; исключением являются случаи, когда P имеет повторяющиеся корни или когда R(x,y) не содержит нечетных степеней y. Однако для каждого эллиптического интеграла существует механизм приведения его к сумме элементарных функций и трёх нормальных эллиптических интегралов (то есть эллиптических интегралов первого, второго и третьего рода).