
- •Лекция 6.
- •1. Основные понятия и теоремы.
- •2. Повторные независимые испытания.
- •2. 1. Биномиальный закон распределения вероятностей.
- •2. 2. Локальная теорема Лапласа.
- •2. 3. Теорема Пуассона.
- •2. 4. Интегральная теорема Лапласа.
- •3. Дискретные случайные величины и их характеристики.
- •4. Непрерывные случайные величины и их характеристики.
- •5. Закон больших чисел.
5. Закон больших чисел.
Закон больших чисел включает в себя неравенство Чебышева, теоре-мы Чебышева и Бернулли.
Сущность закона больших чисел состоит в следующем: при большом числе испытаний случайная величина утрачивает свой случайный характер и становится закономерной величиной.
Неравенство
Чебышева:
Вероятность того, что отклонение
случай-ной величины Х
от ее математического ожидания М(Х)
= а
по абсолютной величине меньше
положительного числа ε,
не меньше чем
![]() ,
то есть
,
то есть
![]() .
.
Основной теоремой закона больших чисел является теорема Чебышева:
Если последовательность попарно независимых случайных величин
![]() имеет конечные
математические ожидания и дисперсии
этих величин равномерно ограничены (
не превышают числа С ), то среднее
арифметическое случайных величин
сходится по вероятности к среднему
арифметическому их математических
ожиданий, то есть для любого малого
положительного числа ε выполняется
неравенство
имеет конечные
математические ожидания и дисперсии
этих величин равномерно ограничены (
не превышают числа С ), то среднее
арифметическое случайных величин
сходится по вероятности к среднему
арифметическому их математических
ожиданий, то есть для любого малого
положительного числа ε выполняется
неравенство
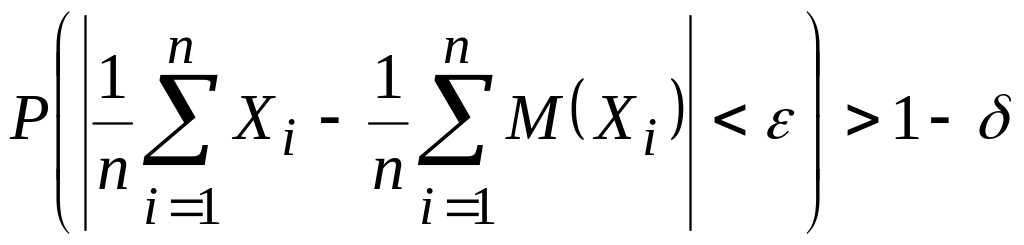
Здесь
![]() ,
где
,
где
![]() -
дисперсия случайной величины Х.
-
дисперсия случайной величины Х.
Теорема Бернулли: При неограниченном увеличении числа испыта-ний частота случайного события сходится по вероятности к вероятности события, то есть
![]() ,
,
где
![]() ,
вероятность р в каждом испытании
постоянна, а
.
,
вероятность р в каждом испытании
постоянна, а
.
Пример 1. В некоторой местности всхожесть семян пшеницы состав-ляет 90 %. Требуется: 1) оценить вероятность того, что при посеве 2000 семян абсолютная величина отклонения частости взошедших семян от ве-роятности их всхожести будет меньше 0,05; 2) сколько нужно посеять се-мян, чтобы с вероятностью 0,95 можно было утверждать, что отклонение частости взошедших семян от вероятности не превышает 0,05?
Решение.
Из условия задачи имеем
![]()
1) Искомую вероятность оценим по теореме Бернулли:
![]() .
.
Отсюда
![]() .
.
2) По условию задачи имеем
![]() ,
отсюда
,
отсюда
![]() ,
,
![]() .
.
Пример 2. В хозяйстве для определения средней урожайности зерно-вых на площади 10000 га взято на выборку по одному квадратному метру с каждого гектара. Какое отклонение средней выборочной урожайности по всей площади можно гарантировать с вероятностью, превышающей 0,9, если дисперсия урожайности по каждому гектару не превышает 30 ц ?
Решение.
Применим теорему Чебышева 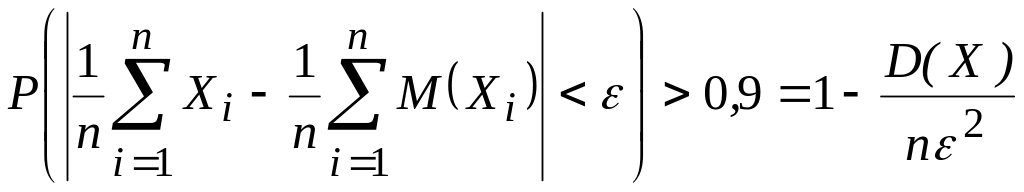 .
.
Отсюда
![]() ,
,
![]() .
.
