4. Непрерывные случайные величины и их характеристики.
Случайная величина называется непрерывной, если ее значения цели-
ком заполняют некоторый конечный или бесконечный интервал числовой
оси.
Пример. Температура Х воздуха, меняющаяся в течение суток от
12,5◦ до 23,4◦ - непрерывная случайная величина.
Для характеристики непрерывной случайной величины Х вводится ее
функция
распределения
,
то есть вероятность того, что значение
величины Х
будет меньше числа х.
Эта функция обладает следующими
свойствами:
1.
.
2.
− неубывающая функция, то есть если
,
то
3.
,
.
4. Вероятность того, что значение Х окажется на заданном отрезке
,
определяется формулой
Производная от функции распределения F(x) называется дифферен-
циальной функцией распределения непрерывной случайной величины Х и
обозначается
,
то есть
.
Поэтому F(x) называют интегральной функцией распределения.
Функция
называется плотностью
распределения случайной ве-
личины Х .
Эта функция обладает следующими свойствами:
Функция - неотрицательна.
.
.
.
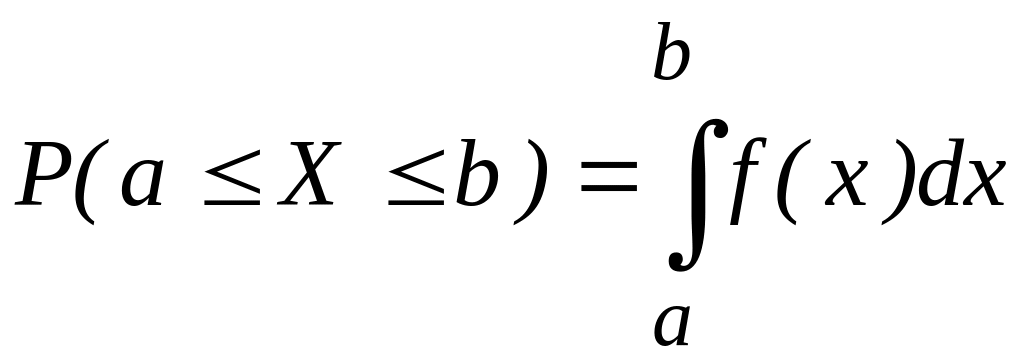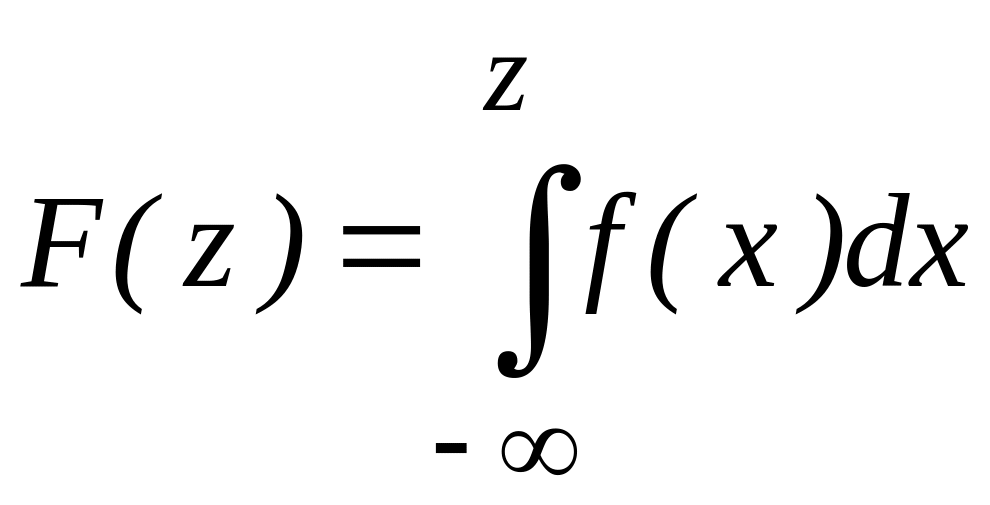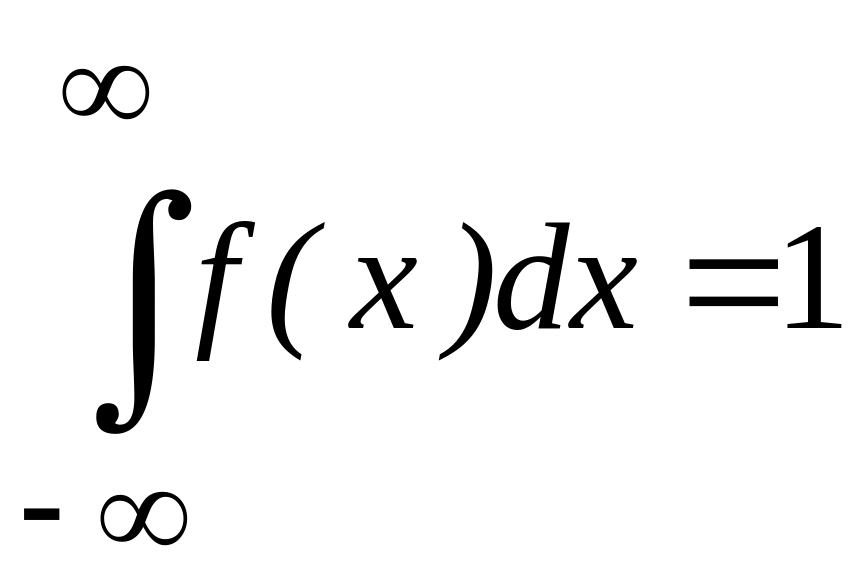Законы распределения непрерывных случайных величин задаются,
как правило, их дифференциальными функциями распределения. На прак-
тике чаще других встречается нормальный закон распределения (закон
Гаусса),
определяемый функцией
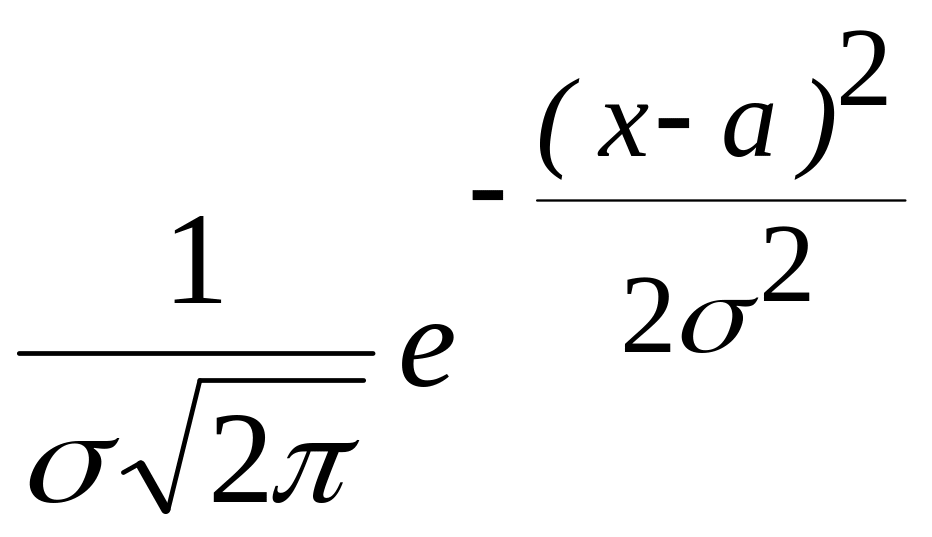, где а
– математическое ожидание,
- среднее квадратическое отклонение
случайной величины.
Математическим ожиданием непрерывной случайной величины Х
на отрезке [a;b] называется среднее ожидаемое значение Х, определяемое
формулой
(4)
Дисперсия
непрерывной
случайной величины Х
на отрезке [a;b]
равна
.
(5)
Среднее квадратическое отклонение
(6)
Пример. Случайная величина Х задана интегральной функцией рас-
пределения
.
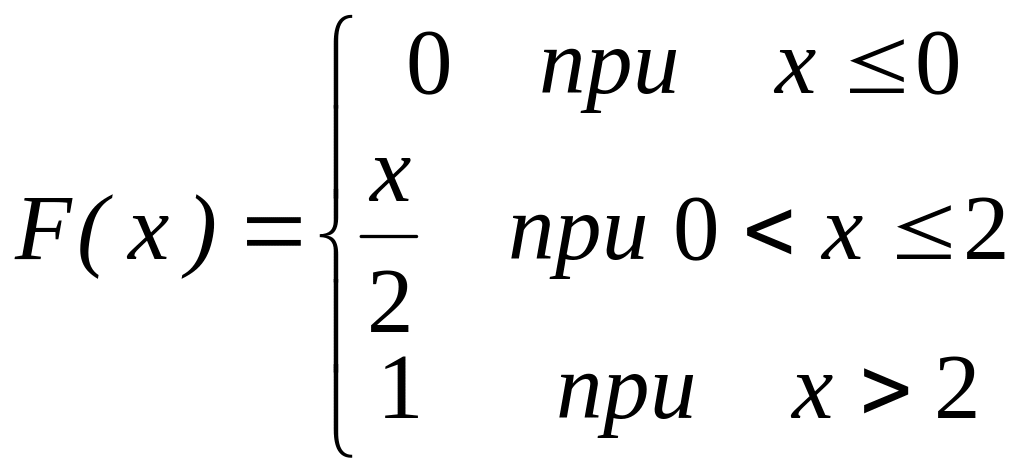Найти: 1) вероятность попадания случайной величины Х в интервал
(0,5; 1,5); 2) дифференциальную функцию распределения ;
3) математическое ожидание М(Х); 4) дисперсию D(X).
Решение. 1). Искомая вероятность равна приращению интегральной
функции на заданном интервале:
.
2). Найдем дифференциальную функцию распределения по
формуле
:
.
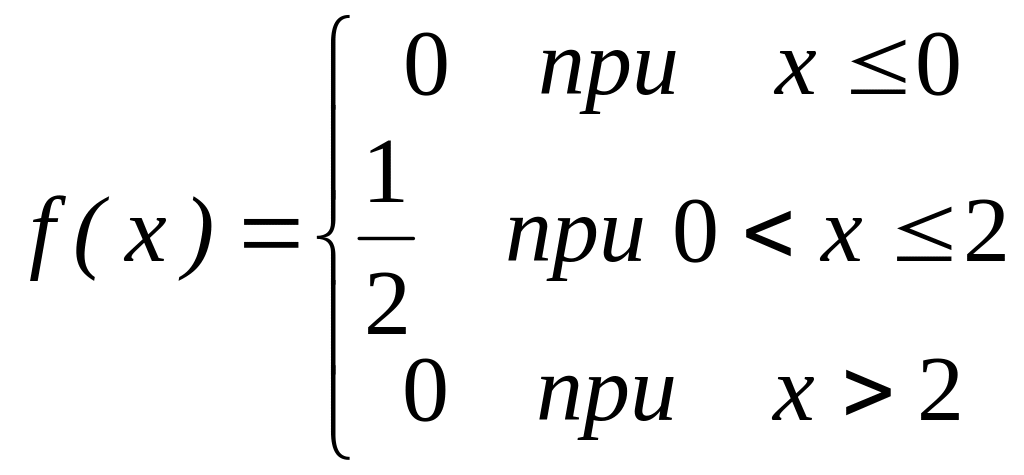3) Математическое ожидание случайной величины Х находим по
формуле (4):
.
4) Дисперсию D(X) определим по формуле (5):
.
Важнейшим из
распределений непрерывной случайной
величины является нормальное
распределение,
задаваемое дифференциальной функ-цией
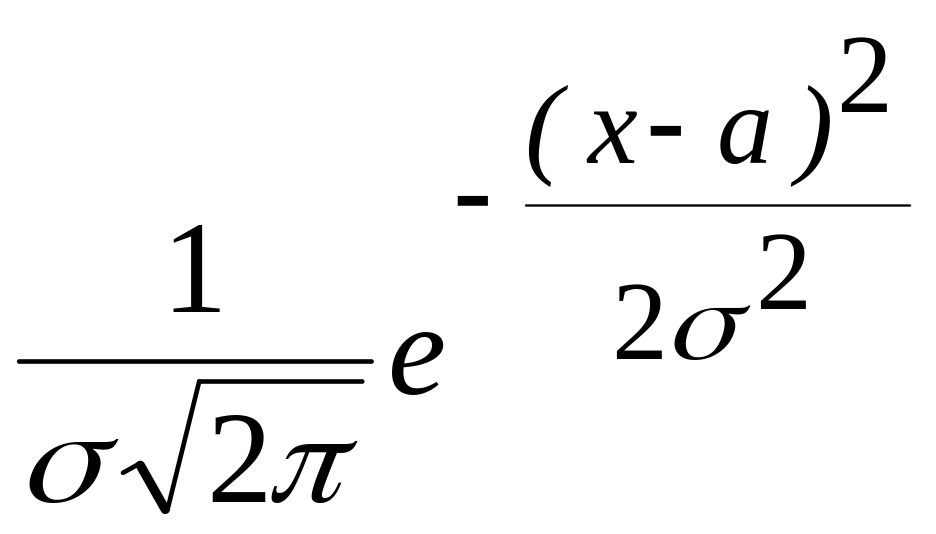, где а
– математическое ожидание,
- среднее квадратическое отклонение
случайной величины.
График функции нормального распределения ( кривая Гаусса) приведен на рис. 2.
Рис. 2
Дифференциальная функция f(x) положительна, имеет максимум
.
Широкое распространение нормального закона распределения объяс-няет теорема Ляпунова, по которой случайная величина Х принимает оп-ределенное значение под воздействием большого числа независимых ма-лых причин, то есть является суммой большого числа независимых случай-ных величин. Закон распределения такой случайной величины близок к нормальному.
Для определения
вероятности того, что случайная величина
Х,
имею-щая нормальное распределение,
принимает значения в интервале
,
применяется формула
.
(7)
Вероятность того, что отклонение нормально распределенной слу-чайной величины Х от ее математического ожидания а не превосходит по-жительного числа ε, вычисляется по формуле
.
(8)
Пример 2. Длина детали представляет собой нормально распреде-ленную случайную величину с математическим ожиданием 40 мм и сред-ним квадратическим отклонением 3 мм. Найти: 1) вероятность того, что длина произвольно взятой детали будет больше 34 мм и и меньше 43 мм; 2) вероятность того, что длина детали отклонится от ее математического ожидания не более чем на 1,5 мм.
Решение. 1) Пусть Х – длина детали. Искомую вероятность найдем по формуле (4), положив в ней а = 40, α = 34, β = 43, σ = 3.
Тогда
.
2) Искомую вероятность найдем по формуле (8):
.
В статистической практике часто используется правило трех сигм
(
),
состоящее в следующем: практически
достоверно, что при испыта-нии абсолютная
величина отклонения нормально
распределенной случай-ной величины Х
от ее математического ожидания
не превзойдет
.
Действительно, из формулы (8) имеем:
.