2. 3. Теорема Пуассона.

При малых значениях вероятности р формула Лапласа дает значи-

тельную погрешность. В этом случае для вычисления вероятности

применяется теорема Пуассона:

Если вероятность р наступления события в каждом испытании пос-

тоянна и близка к нулю, то вероятность наступления этого события

к раз при n испытаниях определяется приближенным равенством

,

где .

Пример. Птицеферма отправила на базу 10000 яиц. Вероятность то-

го, что каждое яйцо повредится в пути, равна 0,0002. Найти вероятность

того, что на базе в отправленной партии яиц окажется три поврежденных

яйца.

Решение. По условию задачи n = 10000; m = 3; р = 0,0002 – мало.

Для вычисления вероятности применим асимптотическую

формулу Пуассона. В нашем случае .

Тогда

.

2. 4. Интегральная теорема Лапласа.

Справедлива следующая теорема, называемая интегральной теоре-

мой Лапласа:

Если вероятность р (0<p<1) наступления события А в каждом испы- тании постоянна, то вероятность того, что событие А появится в n испытаниях от к₁ до к₂ раз вычисляется по приближенной формуле

,

где 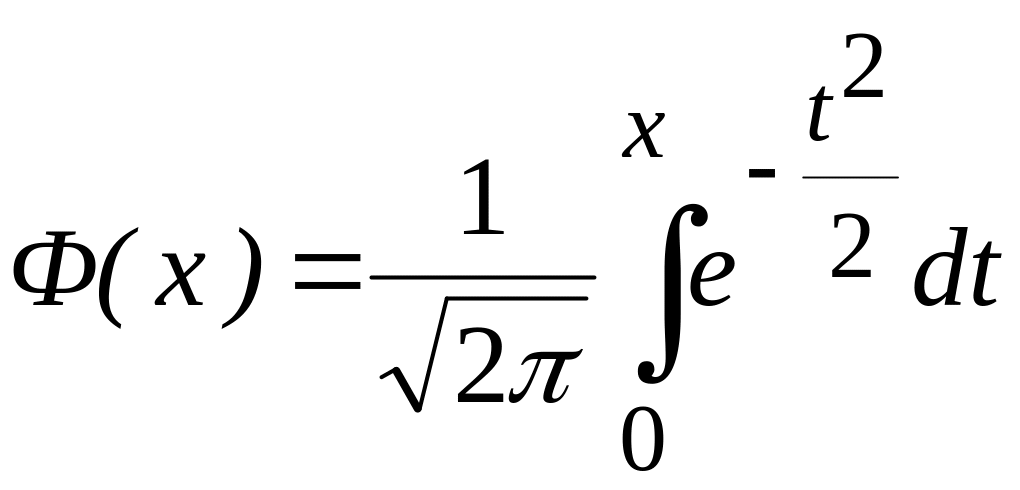− функция Лапласа,

, .

Значения функции Лапласа приводятся в Приложениях, эта функция

нечетная, то есть Ф(− х) = − Ф(х), при х>5 принимается Ф(х) = 0,5.

Пример. Вероятность того, что семя не взойдет, равна 0,2. Найти ве-

роятность того, что среди случайно отобранных 400 семян невсхожих ока-

жется от 70 до 100 семян.

Решение. По условию задачи n = 400; k₁ = 70; k₂ = 100; p = 0,2; q = 0,8.

Находим ; .

Искомая вероятность

.

3. Дискретные случайные величины и их характеристики.

Случайная величина называется дискретной, если она принимает

конечное множество значений или счетное множество значений.

Дискретная случайная величина считается заданной, если известны

вероятности, с которыми она принимает соответствующие числовые значе-

ния.

Пример. Случайная величина Х – число очков от одного до шести, выпадаемых при подбрасывании игральной кости. При этом известны ве-

роятности выпадения различного числа очков при одном подбрасывании,

все они равны . Запишем это в виде следующей таблицы:

Таблица 1

Х	1	2	3	4	5	6
р

Этой таблицей задан закон распределения случайной величины Х.

В общем случае закон распределения случайной величины Х задает-

ся таблицей

Таблица 2

Х			…
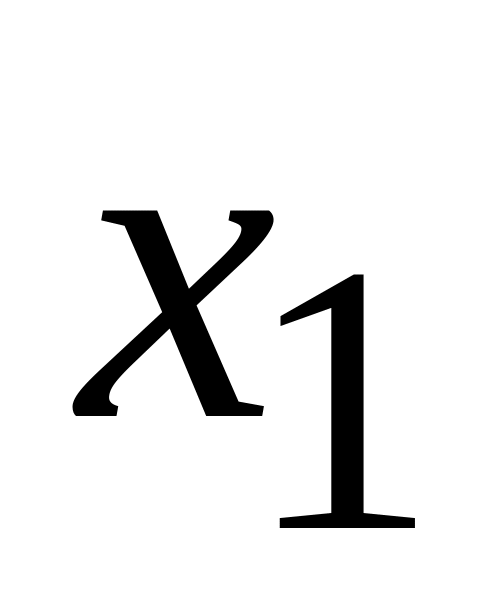
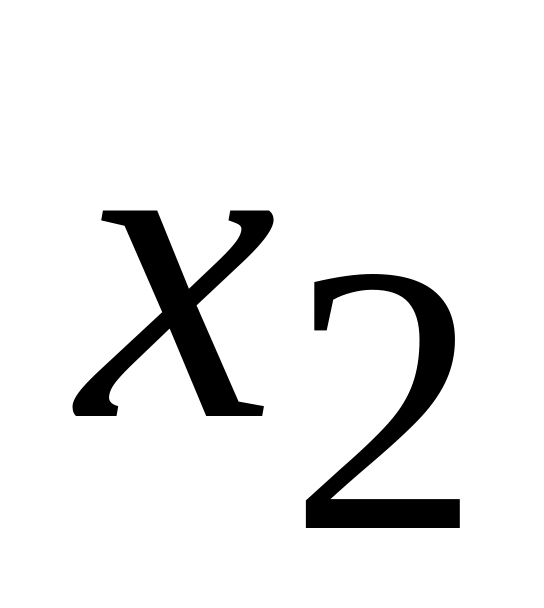
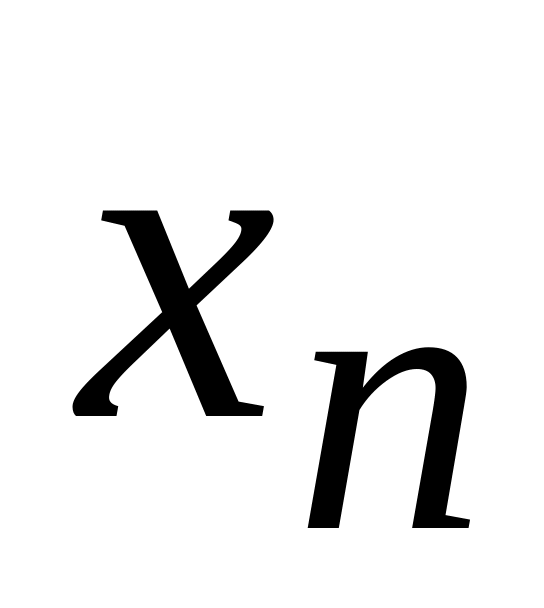
р			…

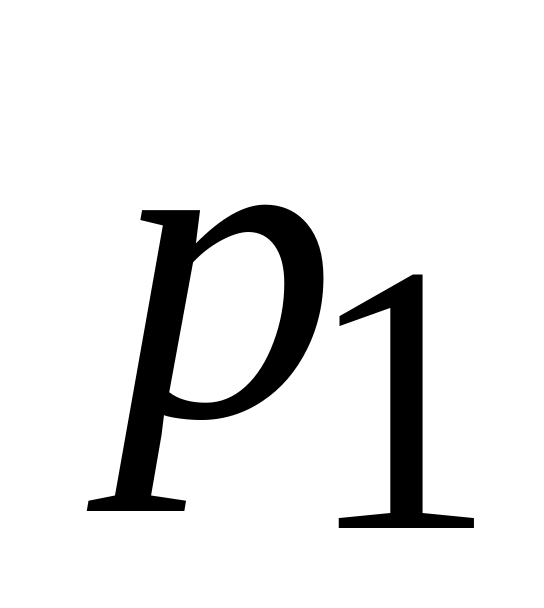
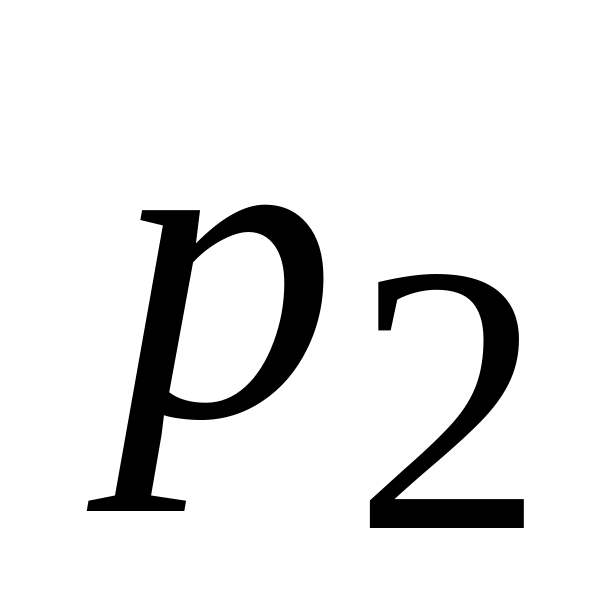
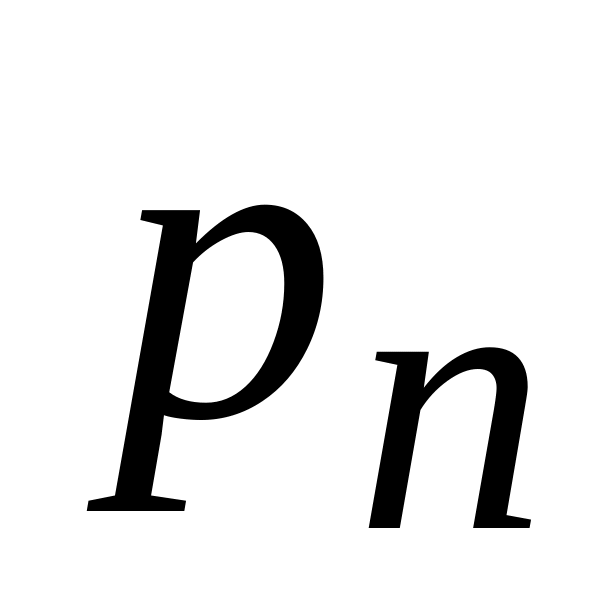
Так как события х₁, х₂, …, х_n образуют полную систему, то .

Математическим ожиданием М(Х) дискретной случайной величины,

заданной приведенной в табл. 2 законом распределения, называется число

М(Х) = . (1)

Дисперсией D(X) дискретной случайной величины называется мате-матическое ожидание квадрата отклонения этой величины от ее математи- ческого ожидания, то есть . (2)

Квадратный корень из дисперсии называется средним квадра- тическим отклонением , то есть

. (3)

Пример. Задан закон распределения дискретной случайной величины Х:

Х 40 42 41 44

р 0,1 0,3 0,2 0,4 .

Найти: 1) математическое ожидание М(Х); 2) дисперсию D(Х); 3) среднее

квадратическое отклонение σ(Х).

Решение. 1) М(Х) =

= 40∙0,1 + 42∙0,3 + 41∙0,2 + 44∙0,4 = 42,4.

2) По формуле (2) имеем:

D(Х) = (40 – 42,4)²∙0,1 + (42 – 42,4)²∙0,3 + (41 – 42,4)²∙0,2 + (44 – 42,4)²∙0,4 =

= 2,04.

Дисперсию D(X) можно вычислить другим способом, исходя из ее

следующего свойства: дисперсия D(X) равна разности между математичес-

ким ожиданием квадрата случайной величины и квадратом ее математи-

ческого ожидания М(Х), то есть .

Для вычисления составим закон распределения величины Х²:

Х² 40² 42² 41² 44²

Р 0,1 0,3 0,2 0,4.

Тогда и

.

3) .