Система автоматизированного моделирования стрелового крана Монография Омск

X X2 X , X

O2

X1

Y1

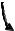
Y

Рис. 2.4. Поворот системы координат на углы Эйлера

Матрица As получена в результате перемножения матриц переноса начала системы координат вдоль каждой из осей системы координат, в которую осуществляется переход [15; 20]:

Матрица Aτ получена в результате перемножения матриц поворота осей координат вокруг каждой из осей системы координат, в которую осуществляется переход [15; 20]:

30

Применение системы однородных координат позволило одной матрицей A (матрицей однородного преобразования) определить преобразование одной локальной системы координат в другую:

ной системе координат (i–1) звена она будет задана вектором [15; 20]

31

где Ai – матрица преобразования систем координат i-го звена в систему координат (i–1) звена.

Любая точка i-го звена, заданная в локальной системе координат этого звена вектором Ri , будет задаваться в инерциальной системе координат вектором [15; 20]:

где Ti - матрица перехода от i-ой локальной системы координат в инерциальную систему координат:

Математическая модель механической подсистемы грузоподъемного крана является системой с нелинейными коэффициентами. Главным упрощением является линеаризация этих коэффициентов, проведенная методом Тейлора. Метод Тейлора позволяет произвести разложение нелинейной функции нескольких переменных по степеням их малых приращений, взятых в окрестностях точки установившегося режима:

q1, q2 , q3 ,. . .– малые приращения переменных, взятые в окрестностях их значений.

При линеаризации уравнений ограничиваются членами первого порядка малости, что приводит к приближенному описанию их линейными дифференциальными уравнениями в малых отклонениях. Для малого отклонения Δf функции f(q1,q2 ,q3,...) будем иметь [15; 20]:

32

Учитывая, что Δf df, Δqj dqj линеаризованные уравнения бу-

дут иметь вид:

В линеаризованном виде векторы характерных точек и векторы скоростей будут иметь вид [15; 20]:

Дифференцирование по формуле (2.2.19) проведем при помощи дифференцирующих матриц [15; 20]:

33

Наиболее распространенным приближенным методом является метод замороженных коэффициентов [21].

Метод замороженных коэффициентов заключается в следующем. Весь рассматриваемый интервал времени работы системы разбивается на участки так, чтобы внутри каждого участка параметры ai изменялись не очень значительно (рис. 2.5).

Для каждого участка времени все коэффициенты дифференциального уравнения считаются постоянными («замороженными») и равными их значениям в начале участка. Внутри каждого участка времени исследуется соответствующее дифференциальное уравнение с постоянными коэффициентами.

ai

Рис. 2.5. Разбиение интервала времени на участки

Решение, полученное методом замороженных коэффициентов, можно уточнить методом последовательных приближений [21].

Рассмотрим систему дифференциальных уравнений с переменными коэффициентами [21]:

Все коэффициенты уравнения (2.2.22) представляются в виде:

где – начало рассматриваемого участка времени.

35

Тогда уравнение (2.2.22) с учетом (2.2.23) имеет вид:

Первое приближение x1 находим по методу замороженных коэффициентов, т.е. решается уравнение:

Остальные решения ищутся как добавки к предыдущим в соответствии с правой частью. Для этого решаются последовательно следующие уравнения с постоянными коэффициентами и с заданной функцией времени в правой части, содержащей найденное предыдущее решение:

a00 ddtnxnk . . . an0xk fk (t ),

где

36

Врезультате получаем уточненное решение дифференциального уравнения с переменными во времени коэффициентами.

Таким образом, предлагается следующая методика автоматизированного построения модели механической подсистемы СГК:

Всоответствии с расчетной схемой СГК задаются следующие параметры звеньев: обобщенные координаты, координаты центров локальных систем координат звеньев, координаты центров масс звеньев, массы звеньев, моменты инерции звеньев, центробежные моменты инерции звеньев, конструктивные параметры звеньев, параметры уп- руго-вязких элементов.

На основе этих данных автоматически строятся уравнения динамики в форме уравнений Лагранжа второго рода с переменными коэффициентами, которые решаются методом замороженных коэффициентов.

2.3.Методика автоматизированного моделирования подсистемы гидропривода стрелового грузоподъемного крана

Несмотря на многообразие схем гидроприводов, количество функциональных элементов гидросистем невелико. К этим элементам относятся: ДВС, гидронасос, гидромотор, гидроцилиндр, гидролиния, разветвление гидролинии, местное сопротивление (дроссель), гидрораспределитель (золотник) [6; 18].

Любую сложную по конфигурации систему гидропривода СГК можно условно расчленить на приведенные выше функциональные элементы, математическое описание которых известно и для которых можно однозначно в рамках рассматриваемой системы определить условия связей между собой.

Математическая модель подсистемы гидропривода составляется при следующих допущениях [11; 17]:

объемный модуль упругости рабочей жидкости в период исследуемого процесса – постоянен;

инерционные свойства потока рабочей жидкости не учитыва-

ются;

волновые процессы в гидроэлементах не учитываются;

37

элементов; p – количество гидроэлементов, составляющих структурную схему гидропривода.

В данной работе предлагается методика составления математических моделей гидроприводов, базирующаяся на представлении схем гидроприводов и их отдельных элементов в виде многомерных динамических объектов, динамические свойства которых характеризуются их матричными передаточными функциями [19].

Fj 1,..., k T [19].

Динамические свойства многомерного объекта полностью определяются его уравнениями движения [8]. Линеаризованная система уравнений движения в векторно-матричной форме имеет вид

где A(s) – квадратная матрица размерности n n; B(s) – прямоугольная матрица размерности n m; C(s) – прямоугольная матрица размерности n k; s – оператор Лапласа.

Линеаризованная математическая модель гидравлического многомерного объекта может рассматриваться как гидравлический многополюсник (ГМП). Таким образом, гидропривод в целом можно рассматривать как результирующий, состоящий из соединенных между собой ГМП. При этом задача математического моделирования сводится к определению результирующих передаточных функций гидропривода. В этом случае модель гидропривода отражает зависимости только между векторами выходных величин и вектором внешних воздействий, исключая векторы, связывающие отдельные ГМП в единую гидросистему.

Математические модели результирующих ГМП разрешены относительно векторов выходных величин [19]:

39