
- •Шкала меры существенности структурных различий по интегральным коэффициентам
- •Определение параметров в генеральной совокупности:
- •2. Определение необходимой численности выборки
- •Определение вероятности, с которой может быть гарантирован результат
- •Обобщающие показатели, характеризующие структурные изменения
- •Выявление факта наличия взаимосвязи между признаками
- •Построение модели регрессии. Оценка адекватности модели
- •Оценка точности прогноза по модели регрессии (слайд 5)
- •Интерпретация результатов построения модели (слайд 7)
- •1. Показатели центра распределения
- •2. Ранговые характеристики (ранговые статистики)
- •3. Показатели дифференциации и концентрации
- •5. Моменты распределения и показатели формы распределения
- •Показатели центра распределения
- •Показатели дифференциации и концентрации
- •Показатели концентрации
- •Показатели вариации
Выявление факта наличия взаимосвязи между признаками
При выявлении факта наличия взаимосвязи между признаками используются как методы основанные на первичных данных (методы 1 и2), так и методы, основанные на группировках (3-5):
Метод параллельных рядов
Поле корреляции
Аналитические группировки (групповая таблица)
Корреляционные таблицы
Простейшим приемом обнаружения связи является сопоставление двух параллельных рядов - ряда значений факторного признака и соответствующих ему значений результативного признака. Значения факторного признака располагают в возрастающем порядке и затем прослеживают направление изменения величины результативного признака. Результативный признак (функцию) в дальнейшем будем обозначать через у, а факторный признак - через х.
Поле корреляции представляет собой графическое изображение первичных данных: по оси абсцисс откладываются значения факторного признака, по оси ординат –результативного. В том случае, если основная часть единиц формирует облако, располагающееся из левого нижнего угла системы координат в правый верхний, можно предположить наличие прямой взаимосвязи между признаками, из левого верхнего угла в правый нижний .- обратной. (СЛАЙД 1, рис 1)
Аналитическая группировка позволяет изучить изменение средних значений результативного признака при изменении факторного признака (СЛАЙД 1). На слайде 1 результат построении аналитической группировки представлен в первой и двух последних графах таблицы. Первая графа – основание группировки – представляет собой группы магазинов по доле покупателей в возрасте от 25 до 40 лет, в двух последних графах представлено число магазинов в каждой группе и средняя цена на реализуемый товар. Соответственно представляется возможным проследит тенденцию в изменении средней цены при росте доли покупателей. Графическое изображение этой зависимости называется эмпирическая линия регрессии и представлено на рис.2 СЛАЙДА 1.
При построении корреляционной таблицы группировка осуществляется одновременно и по факторному и по результативному признаку, а на пересечении строк и столбцов проставляется количество единиц совокупности одновременно имеющих определенные значения факторного и результативного признаков. . На СЛАЙДЕ 1 расположение частот (в осеновном вокруг главной диагонали таблицы) свидетельствует о возможном наличии прямой взаимосвязи между признаками.
Система показателей степени тесноты взаимосвязи (дается краткая характеристика основных показателей) СЛАЙД 2
Показатели степени тесноты связи дают возможность охарактеризовать зависимость вариации результативного признака от вариации признака-фактора. В известной мере они дополняют и развивают уже отмеченные приемы обнаружения связи.
Зная показатели тесноты корреляционной связи, мы можем решать следующие группы вопросов:
1) ответить на вопрос о необходимости изучения данной связи между признаками и целесообразности ее практического применения;
2) сопоставляя показатели тесноты связи для различных ситуаций, можно судить о степени различий в ее проявлении для конкретных условий;
3) и, наконец, сопоставляя показатели тесноты связи результативного признака с различными факторами, можно выявить те факторы, которые в конкретных условиях являются решающими и главным образом воздействуют на формирование величины результативного признака.
К простейшим показателям степени тесноты связи относят коэффициент корреляции знаков, который был предложен немецким ученым Г. Фехнером (1801-1887). Этот показатель основан на оценке степени согласованности направлений отклонений индивидуальных значений факторного и результативного признаков от соответствующих средних. Для его расчета вычисляют средние значения результативного и факторного признаков, а затем проставляют знаки отклонений для всех значений взаимосвязанных пар признаков
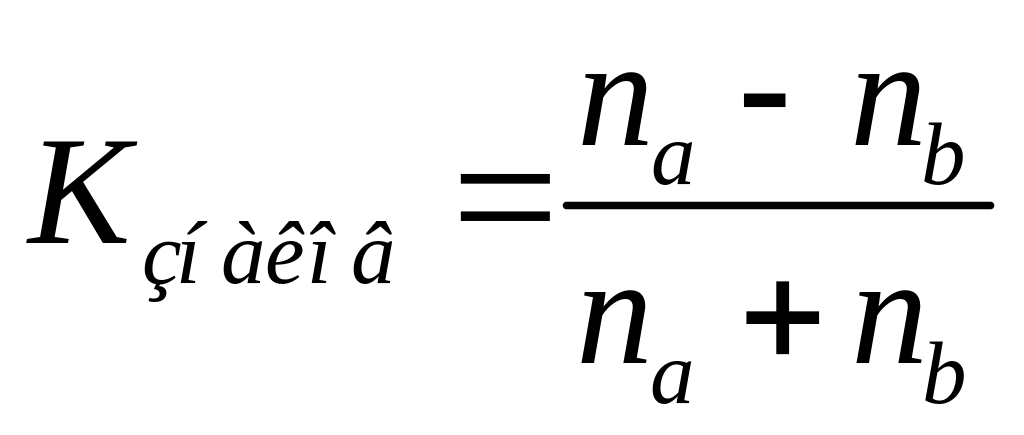 ,
,
![]() – число совпадений знаков отклонений
значений факторного и результативного
признаков от соответствующей средней
– число совпадений знаков отклонений
значений факторного и результативного
признаков от соответствующей средней
![]() - число несовпадений знаков отклонений
значений факторного и результативного
признаков от соответствующей средней
- число несовпадений знаков отклонений
значений факторного и результативного
признаков от соответствующей средней
Как и все коэффициенты корреляции коэффициент корреляции знаков изменяется от -1 до +1. Знак показывает направление взаимосвязи, абсолютная величина – степень тесноты взаимосвязи. Основной недостаток данного показателя: он всегда будет равен нулю при равенстве числа совпадений и несовпадений знаков.
Более совершенным показателем степени тесноты связи является линейный коэффициент корреляции (r)1.
При
расчете этого показателя учитываются
не только знаки отклонений индивидуальных
значений признака от средней, но и сама
величина таких отклонений, т.е.
соответственно для факторного и
результативного признаков определяют
величины
![]() и
и
![]() .
Однако непосредственно сопоставлять
между собой полученные абсолютные
величины нельзя, так как сами признаки
могут быть выражены в разных единицах
(как это имеет место в представленном
примере), а при наличии одних и тех же
единиц измерения средние могут быть
различны по величине. В этой связи
сравнению могут подлежать отклонения,
выраженные в относительных величинах
(их называют нормированными отклонениями).
Так, для факторного признака будем иметь
совокупность величин
.
Однако непосредственно сопоставлять
между собой полученные абсолютные
величины нельзя, так как сами признаки
могут быть выражены в разных единицах
(как это имеет место в представленном
примере), а при наличии одних и тех же
единиц измерения средние могут быть
различны по величине. В этой связи
сравнению могут подлежать отклонения,
выраженные в относительных величинах
(их называют нормированными отклонениями).
Так, для факторного признака будем иметь
совокупность величин
![]() ,
а для результативного
,
а для результативного
![]() .
.
Полученные нормированные отклонения можно сравнивать между собой. Для того чтобы на основе сопоставления рассчитанных нормированных отклонений получить обобщающую характеристику степени тесноты связи между признаками для всей совокупности, рассчитывают среднюю величину произведений нормированных отклонений. Полученная таким образом средняя и будет являться линейным коэффициентом корреляции r.
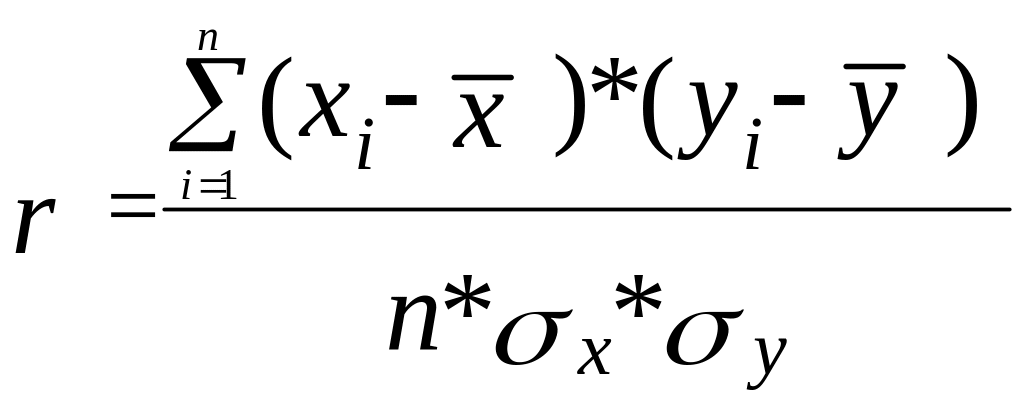
Линейный коэффициент корреляции может принимать любые значения в пределах от -1 до +1. Чем ближе коэффициент корреляции по абсолютной величине к 1, тем теснее связь между признаками. Знак при линейном коэффициенте корреляции указывает на направление связи - прямой зависимости соответствует знак "плюс", а обратной зависимости - знак минус.
Если с увеличением значений факторного признака результативный признак имеет тенденцию к увеличению, то величина коэффициента корреляции будет находиться между 0 и 1. Если же с увеличением значений х результативный признак у имеет тенденцию к снижению, коэффициент корреляции может принимать значения в интервале от 0 до -1.
При оценке степени тесноты связи с помощью коэффициента корреляции она производится, как правило, на основе более или менее ограниченной информации об изучаемом явлении. Возникает вопрос, насколько правомерно наше заключение по выборочным данным в отношении действительного наличия корреляционной связи в той генеральной совокупности, из которой была произведена выборка?
Следовательно возникает необходимость проверки существенности коэффициента корреляции.
1. При большом объеме выборки определяется отношение коэффициента корреляции к его среднеквадратической ошибке
 ,
где
,
где
![]()
Если величина линейного коэффициента
корреляции превышает величину средней
квадратической ошибки более, чем в
![]() раз, то можно говорить о существенности
выборочного коэффициента корреляции,
где
раз, то можно говорить о существенности
выборочного коэффициента корреляции,
где
![]() - уровень значимости 0,01 или 0,05. Если
отношение
- уровень значимости 0,01 или 0,05. Если
отношение
![]() окажется меньше
,
то с вероятностью
окажется меньше
,
то с вероятностью
![]() следует предполагать отсутствие
корреляционной связи в генеральной
совокупности. Сравнение выполняется с
табличным значением t-критерия Лапласа.
следует предполагать отсутствие
корреляционной связи в генеральной
совокупности. Сравнение выполняется с
табличным значением t-критерия Лапласа.
2. При малых объемах выборки используется
тот факт, что величина
![]() при условии r=0, распределена по
закону Стьюдента с (n-2)
степенями свободы.
при условии r=0, распределена по
закону Стьюдента с (n-2)
степенями свободы.
Полученную величину tрасч. сравнивают с табличным значением t-критерия (число степеней свободы равно n - 2). Если рассчитанная величина превосходит табличное значение критерия t, то практически невероятно, что найденное значение обусловлено только случайными совпадениями х и у в выборке из генеральной совокупности, для которой действительное значение коэффициента корреляции равно нулю. Если же вычисленная величина tрасч. меньше, чем в таблице, то полагают, что коэффициент корреляции в генеральной совокупности в действительности равен нулю и соответственно эмпирический коэффициент корреляции существенно не отличается от нуля.
Коэффициент корреляции достаточно
точно оценивает степень тесноты связи
лишь в случае наличия линейной зависимости
между признаками. При наличии же
криволинейной зависимости линейный
коэффициент корреляции недооценивает
степень тесноты связи и даже может быть
равен 0, а потому в таких
случаях рекомендуется использовать в
качестве показателя степени тесноты
связи эмпирическое корреляционное
отношение
![]() .
.
Расчет корреляционного отношения основан на использовании известной теоремы сложения дисперсий.

Значимость рассчитанного корреляционного отношения оценивается с помощью дисперсионного отношения
![]() .
.
Если фактор, положенный в основу
группировки, не оказывает влияния на
вариацию изучаемого признака, то
межгрупповая дисперсия будет отражать
влияние тех же прочих факторов, которые
определяют и вариацию внутри групп, а
потому отношение дисперсий будет близко
к 1 или отличаться от нее в силу наличия
случайных колебаний. В таблицах
F-распределения
указывают предельные значения F-критерия
для различных комбинаций числа степеней
свободы
![]() и
и
![]() ,
которые могут быть превзойдены с
вероятностью 0,05 или 0,01 в силу случайных
обстоятельств.
,
которые могут быть превзойдены с
вероятностью 0,05 или 0,01 в силу случайных
обстоятельств.
Следует отметить, что вычисление корреляционного отношения возможно лишь при наличии достаточно большого числа данных, которые представлены либо в форме корреляционной, либо в форме групповой таблицы. Вычисление корреляционного отношения при большом числе групп и малом числе наблюдений в каждой группе лишается смысла.
Использование линейного коэффициента корреляции и корреляционного отношения при проверке возможности использования линейной функции в качестве формы взаимосвязи
Сопоставление линейного коэффициента корреляции и эмпирического корреляционного отношения имеет смысл только в случае, если эти показатели вычислены для одинаковым образом сгруппированных данных, т.е. при сравнении и коэффициент корреляции, и корреляционное отношение должны быть вычислены либо по данным корреляционной таблицы, либо по первичным данным и групповой таблице, что предпочтительнее.
При проверке возможности использования
линейной функции в качестве формы
уравнения определяют разность квадратов
![]() ,
и если эта разность менее
0,1, то считается возможным применять
линейное уравнение корреляционной
зависимости.
,
и если эта разность менее
0,1, то считается возможным применять
линейное уравнение корреляционной
зависимости.
Для проверки гипотезы о линейной зависимости более эффективно использование величины w2:
![]() ,
,
которая, подчиняется закону F-распределения с числом степеней свободы числителя (k-2) и знаменателя (n-k).
Задаваясь достаточно малым уровнем значимости (например, = 0,05), находим по таблицам F-распределения значение Fтабл при заданной величине и соответствующем числе степеней свободы.
Непараметрические показатели тесноты взаимосвязи. Ранговые коэффициенты корреляции. (СЛАЙДЫ 2 и 3)
Применение линейного коэффициента корреляции для оценки степени тесноты связи между признаками особенно в той части, которая связана с оценкой его существенности, является обоснованным лишь в условиях нормального или близкого к нормальному распределению признаков в изучаемой совокупности.
Кроме того, как видно из приводимых выше формул, для определения величины линейного коэффициента корреляции необходимо знать численные значения факторного и результативного признаков. В некоторых же случаях мы можем встретиться с такими качествами, которые не поддаются выражению числом единиц.
Эти обстоятельства заставляют прибегать к использованию так называемых непараметрических методов, позволяющих измерить интенсивность связи как между количественными признаками, форма распределения которых отличается от нормальной, так и между качественными признаками. В основу непараметрических методов положен принцип нумерации значений статистического ряда. Каждой единице совокупности присваивается порядковый номер в ряду, который будет упорядочен по уровню признака. Таким образом, ряд значений признака ранжируется, а номер каждой отдельной единицы будет ее рангом. (формулы приведены на СЛАЙДЕ 2, пример расчета – на СЛАЙДЕ 3)
Коэффициенты корреляции, основанные на использовании рангов, были предложены К. Спирмэном и М. Кендэлом. Коэффициент корреляции рангов Спирмэна (был использован им в начале XX в.) основан на рассмотрении разности рангов значений факторного и результативного признаков.
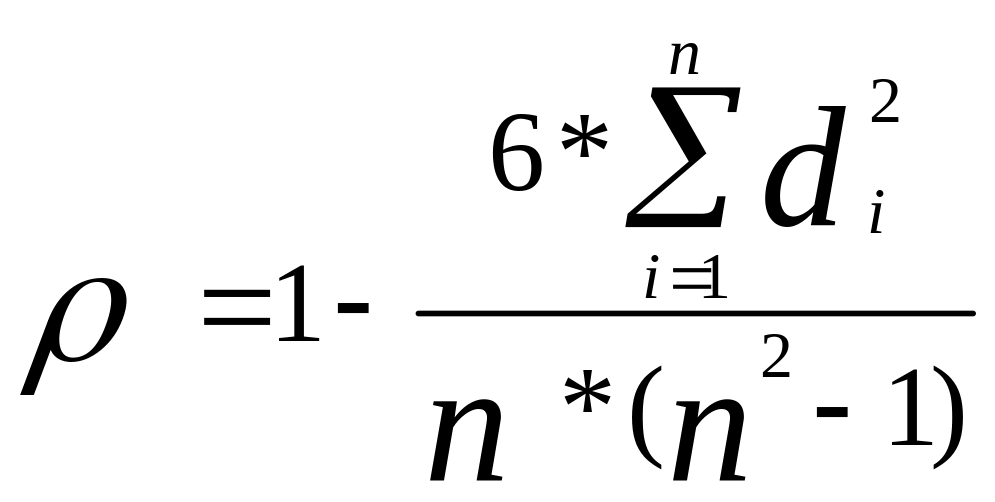
![]() – разность рангов факторного и
результативного признаков
– разность рангов факторного и
результативного признаков
М. Кендэл предложил еще одну меру связи
между переменными х и у
- коэффициент
корреляции рангов Кендэла
-
![]() :
:
![]() ,
,
где P – характеризует соответствие рангов факторного и результативного признаков и определяется как число единиц совокупности ранг которых больше данного (определяется по неупорядоченному ряду рангов).
Q- характеризует несоответствие рангов факторного и результативного признаков и определяется как число единиц совокупности ранг которых меньше данного (определяется по неупорядоченному ряду рангов).
Для вычисления надо упорядочить ряд рангов переменной х, приведя его к ряду натуральных чисел.
САМОСТОЯТЕЛЬНО необходимо изучить показатели степени тесноты взаимосвязи между качественными признаками
