
- •2.Основные числовые мн-ва, примеры. Вещественные числа.
- •3.Ограниченные и неограниченные числовые мн-ва, точные верхние и нижние грани мн-тв; теорема о существовании точной верхней(нижней) грани у ограниченного сверху(снизу) мн-ва.
- •6.Сходящиеся посл-ти: определение предела посл-ти, основные св-ва сходящихся посл-тей. Сходящиеся пос-ти.
- •8.Понятие ф-ции. Область определения, мн-во значений, способы задания. Простейшие элементарные ф-ции. Понятия функции.
- •9.Предел ф-ции в точке: определение предела ф-ции по Каши и по Гейне, эквивалентность двух определений. Предел функций.
- •10.Односторонние пределы. Св-ва ф-ций, имеющих предел: арифметические операции, предельный переход в неравенствах. Понятие одностороннего предела.
- •14.Точки разрыва, их классификация, примеры.
14.Точки разрыва, их классификация, примеры.
Опр.
Если ф-ция f(x)
не обладает в т.а св-вами непрерывности
(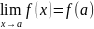 ),
то т.а наз точкой разрыва f(x).Все
точки разрыва делятся на три типа:
–Точка а наз. точкой устранимого разрыва
ф-ции
если она имеет в точке а предел, но этот
предел не равен частному значению ф-ции
в этой точке( либо ф-ции
в точке а не определена т.е.
не
существует).пример f(x)=
),
то т.а наз точкой разрыва f(x).Все
точки разрыва делятся на три типа:
–Точка а наз. точкой устранимого разрыва
ф-ции
если она имеет в точке а предел, но этот
предел не равен частному значению ф-ции
в этой точке( либо ф-ции
в точке а не определена т.е.
не
существует).пример f(x)=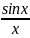 разрыв в т.. х=0
разрыв в т.. х=0
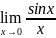 =1
=1
Если а точка устранимого разрыва, то этот разрыв можно устранить, доопределив ф-цию в точке разрыва или изменив значение ф-ции в точке разрыва.
–точка
а наз.точкой разрыва первого рода если
имеет в точке конечные правый и левый
пределы не равные между собой. Пример:
f(x)=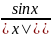 разрыв в т. Х=0
разрыв в т. Х=0
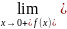 =
=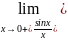 =1-правый
=1-правый
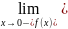 =
=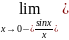 =-1
–левый
=-1
–левый
– точка
а наз. точкой разрыва второго рода ф-ции
если
хотя бы один из односторонних пределов
не существует или равен ∞. Пример:
f(x)=sin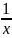 x=0
т.разрыва
x=0
т.разрыва
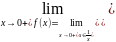 =Sin(+∞)
–не существует.
=Sin(+∞)
–не существует.
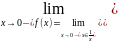 =-Sin(+∞)
–не существует.
=-Sin(+∞)
–не существует.
f(x)=
x=0
т. Разрыва
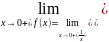 =+∞
=+∞
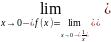 =-∞.
=-∞.
15.Св-ва
ф-ций, непрерывных на отрезке: теорема
о прохождении непрерывной ф-ции через
нуль при смене знаков, теорема о
прохождении непрерывной ф-ции через
любое промежуточное значение.
1.Теорема через любое значение: Пусть
y=
непрерывна [a,b]
и значение на концах отрезка
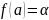 ,
,
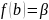 .
Тогда любые числа ν, заключенного между
α и β, существует т.сЄ[a,b]
такая что
.
Тогда любые числа ν, заключенного между
α и β, существует т.сЄ[a,b]
такая что
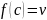 .
.
2.Терорема
через нуль:если ф-ция
непрерывна на отрезке [a,b]
и значения на отрезках
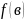 ,
имеет разные значения то внутри [a,b]
существует т.с такая что
,
имеет разные значения то внутри [a,b]
существует т.с такая что

16.Ограниченность
функции, непрерывной на отрезке, первая
теорема Вейерштрасса. Точные грани
функции, вторая теорема Вейерштрасса(о
достижении граней функцией, непрерывной
на отрезке).
. Если
ф-ция y=
непрерывна
на отрезке [a,b]
то эта ф-ция ограничена на этом отрезке.
Ф-ция y=
ограничена сверху(снизу) на множестве
Х если существует число М(м) такое что
для любого хЄХ выполняется х≤М(х≥м).
Ф-ция наз. ограниченной если она
ограниченна и сверху и снизу. 2. Если
ф-ция y=
непрерывна
на отрезке [a,b]
то среди ее значений на этом отрезке
имеются значения равные точкой нижней
гранью м, и точкой верхней гранью М, т.е.
существует т.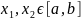 такие
что f(
такие
что f(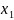 )=
)=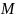 f(
f(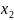 )=m.
)=m.
17.Монотонные
ф-ции, понятие обратной ф-ции, теорема
о существовании и непрерывности обратной
ф-ции. Обратные тригонометрические
ф-ции.
опр.
Ф-ция y=
наз. неубывающей(невозрастающей) на
множестве Х, если для любых двух элементов
этого множества таких что
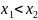 выполняються f(
)≤
f(
)(
f(
)≥
f(
)).
Опр. Ф-ция наз. монотонной если она
является неубывающей или не возрастающей.
Опр. Ф-ция наз. Монотонной если она
является неубывающей или невозрастающей.
Обратные ф-ции: Пусть y=f(x)
определена на[a,b].
Пусть f(a)=α,
f(b)=β,
т.е. область значений [α,β]. Пусть любое
yє[α,β]
отвечает единственное значение xє[a,b]
такое что f(x)=y
тогда говорят что на отрезке [α,β]
определенна ф-ция x=f-1(y)
обратная к ф-ции =f(x).
Пример: =x2
на отрезке [0,2] область значений [0,4] на
[0,4] определена ф-цией x=
выполняються f(
)≤
f(
)(
f(
)≥
f(
)).
Опр. Ф-ция наз. монотонной если она
является неубывающей или не возрастающей.
Опр. Ф-ция наз. Монотонной если она
является неубывающей или невозрастающей.
Обратные ф-ции: Пусть y=f(x)
определена на[a,b].
Пусть f(a)=α,
f(b)=β,
т.е. область значений [α,β]. Пусть любое
yє[α,β]
отвечает единственное значение xє[a,b]
такое что f(x)=y
тогда говорят что на отрезке [α,β]
определенна ф-ция x=f-1(y)
обратная к ф-ции =f(x).
Пример: =x2
на отрезке [0,2] область значений [0,4] на
[0,4] определена ф-цией x=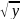 .
Теорема: Пусть ф-ция y=f(x)
возрастает(убывает) на [a,b]
и непрерывна на этом отрезке. Пустьf
(a)=α,
f(b)=β.
Тогда на отрезке [α,β]([β,α])
определена обратная ф-ция для y=f(x)
ф-ция x=f-1(y),
которая возрастает(убывает) и непрерывна
на указанном отрезке. Замечание:
определение обратной ф-ции аналогичным
образом можно дать для любого мн-ва х.
.
Теорема: Пусть ф-ция y=f(x)
возрастает(убывает) на [a,b]
и непрерывна на этом отрезке. Пустьf
(a)=α,
f(b)=β.
Тогда на отрезке [α,β]([β,α])
определена обратная ф-ция для y=f(x)
ф-ция x=f-1(y),
которая возрастает(убывает) и непрерывна
на указанном отрезке. Замечание:
определение обратной ф-ции аналогичным
образом можно дать для любого мн-ва х.
