
- •Основные числовые множества
- •Операции над множествами
- •Свойства операций над множествами
- •Предел последовательности
- •[Править] Некоторые виды последовательностей
- •[Править] Ограниченные и неограниченные последовательности
- •Бесконечно большие и бесконечно малые последовательности
- •[Править] Свойства бесконечно малых последовательностей
- •Свойства числовых последовательностей.
- •Евклидово пространство
- •Поведение функций [править] Сюръективность
- •[Править] Инъективность
- •Предел числовой последовательности
Евклидово пространство
Править
В математике термин евкли́дово простра́нство может обозначать один из двух сходных объектов:
1. Конечномерное вещественное векторное пространство с введённой на нём нормой
где . Также назывется конечномерным гильбертовым пространством
2. Метрическое пространство, которое является конечномерным векторным пространством над полем вещественных чисел с метрикой, введённой по формуле:
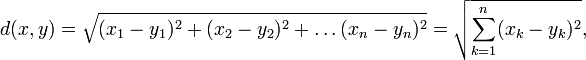
где
и
![]()
Наглядными
примерами евклидовых пространств могут
служить пространства
![]() размерности
n = 1 (вещественная прямая) и
размерности
n = 1 (вещественная прямая) и
![]() размерности
n = 2 (комплексная плоскость или
евклидова плоскость).
размерности
n = 2 (комплексная плоскость или
евклидова плоскость).
5. Введем понятие
окрестности точки. Окрестностью
точки a называется любой интервал,
содержащий эту точку. Например, интервал
(2; 6) - это окрестность точки 3.
Посмотрим
на график на рисунке ниже.
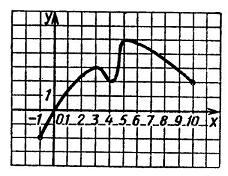 Наиболее
заметными точками области определения
являются точки x, в которых возрастание
сменяется убыванием (точки 3 и 5) или
убывание сменяется возрастанием (точка
4). Эти точки называют соответственно
точками максимума (xmax=3; xmax=5)
и точками минимума (xmin=4).
При
построении графиков функций полезно
сначала найти точки максимума и минимума.
Например, в случае функции синуса точки
вида π/2+2πn - это точки максимума, а точки
вида -π/2+2πn - это точки минимума.
В
дальнейшем изложении будет показано,
как искать
точки максимума и минимума функции,
не прибегая к рисованию графиков.Точки
максимума и минимума функции называют
точками экстремума функции.
Наиболее
заметными точками области определения
являются точки x, в которых возрастание
сменяется убыванием (точки 3 и 5) или
убывание сменяется возрастанием (точка
4). Эти точки называют соответственно
точками максимума (xmax=3; xmax=5)
и точками минимума (xmin=4).
При
построении графиков функций полезно
сначала найти точки максимума и минимума.
Например, в случае функции синуса точки
вида π/2+2πn - это точки максимума, а точки
вида -π/2+2πn - это точки минимума.
В
дальнейшем изложении будет показано,
как искать
точки максимума и минимума функции,
не прибегая к рисованию графиков.Точки
максимума и минимума функции называют
точками экстремума функции.
Окре́стность точки — множество, содержащее данную точку, и близкие (в каком-либо смысле) к ней. В разных разделах математики это понятие определяется по-разному.
Содержание [показать] |
[править] Определения
[править] Математический анализ
Основная статья: ε-окрестность
Пусть ε > 0 произвольное фиксированное число.
Окрестностью точки x0 на числовой прямой (иногда говорят ε-окрестностью) называется множество точек, удаленных от x0 не более чем на ε, т.е. Oε(x0) = {x: | x − x0 | < ε}.
В многомерном случае роль окрестности выполняет открытый ε-шар с центром в точке x0.
В
банаховом
пространстве
![]() окрестностью
с центром в точке x0
называют множество
окрестностью
с центром в точке x0
называют множество
![]() .
.
В
метрическом
пространстве
(M,ρ)
окрестностью с центром в точке y
называют множество
![]() .
.
[править] Общая топология
Пусть задано топологическое пространство
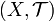 ,
где X
— произвольное множество,
а
,
где X
— произвольное множество,
а
 —
определённая на X
топология.
Множество
—
определённая на X
топология.
Множество
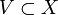 называется
окрестностью точки
называется
окрестностью точки
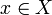 ,
если существует открытое
множество
,
если существует открытое
множество
 такое,
что
такое,
что
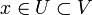 .
.
Аналогично окрестностью множества
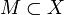 называется
такое множество
,
что существует открытое множество
,
для которого выполнено
называется
такое множество
,
что существует открытое множество
,
для которого выполнено
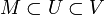 .
.
[править] Замечания

В Викисловаре есть статья «окрестность»
Приведённые выше определения не требуют, чтобы окрестность V была открытым множеством, но лишь чтобы она содержала открытое множество U. Некоторые авторы настаивают на том, что любая окрестность открыта. [1] Тогда окрестностью множества называется любое содержащее его открытое множество. Это не принципиальное для развития дальнейшей топологической теории различие. Однако в каждом случае важно фиксировать терминологию.
Прямо из определения следует, что V является окрестностью множества M тогда и только тогда, когда V есть окрестность любой точки
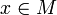 .
.
[править] Пример
Пусть дана вещественная прямая со стандартной топологией. Тогда ( − 1,2) является открытой окрестностью, а [ − 1,2] — замкнутой окрестностью точки 0.
[править] Вариации и обобщения
[править] Проколотая окрестность
Множество
![]() называется
проко́лотой
окре́стностью
(вы́колотой окрестностью) точки
,
если
называется
проко́лотой
окре́стностью
(вы́колотой окрестностью) точки
,
если
![]()
где V — окрестность x.
Строго говоря, проколотая окрестность не является окрестностью в смысле данного выше определения. Проще говоря, проколотой окрестностью точки называется окрестность точки, из которой исключена эта точка.
6. Обозначения
Если задана функция f, которая определена на множестве X и принимает значения в множестве Y, то есть, функция f отображает множество X в Y, то
этот факт коротко записывают в виде
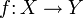 или
или
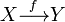 .
.область определения функции f (множество X) обозначается D(f), или
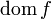 ;
;область значений функции f (множество Y) обозначается R(f) (E(f)), или
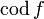 (
(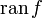 ).
).
Наличие
функциональной зависимости между
элементом
и
элементом
![]()
наиболее часто обозначается как
y = f(x),
![]() или
или
![]() ;
;
реже используется обозначение без скобок y = fx,
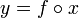 или
y
= xf,
или
y
= xf,а там, где необходимо подчеркнуть двойственность, используются обозначения со скобками: y = (f,x) или y = (x,f);
так же существует и операторное обозначение y = xf, которое можно встретить в общей алгебре.
λx.y в лямбда-исчислении Чёрча.
[править] Функции нескольких аргументов
Определение функции легко обобщить на случай функции многих аргументов.
Если
множество X
представляет собой декартово
произведение
множеств
![]() ,
тогда отображение
оказывается
n-местным
отображением, при этом элементы
упорядоченного набора
,
тогда отображение
оказывается
n-местным
отображением, при этом элементы
упорядоченного набора
![]() называются
аргументами (данной n-местной
функции), каждый из которых пробегает
своё множество:
называются
аргументами (данной n-местной
функции), каждый из которых пробегает
своё множество:
![]() где
где
![]() .
.
В
этом случае y
= f(x)
означает, что
![]() .
.
