4.7.Потоковые методы

4.7.1.Использование колец Гельмгольца и способ параллелепипеда

Сущность метода заключается в том, что в объект вносится в кольца Гельмгольца (рис. 4.9).

R

Х

Рис.4.9. Использование колец Гельмгольца

К кольцам подключен микровеберметр, по показаниям которого при извлечении объекта их колей Гельмгольца в направлении оси Х определяется величина магнитного момента . Данный способ позволяет определить только одну компоненту магнитного момента [15].

В методе параллелепипеда три взаимно ортогональных обмотки расположены на каркасе призматической формы, конструкция которого позволяет открывать одну или несколько граней для помещения внутрь измеряемого объекта без нарушения целостности обмоток. При внесении объекта внутрь параллелепипеда на взаимно ортогональных обмотках появляются ЭДС пропорциональные величинам соответствующих компонент магнитного момента [16].

4.7.2.Общие соотношения для потокового метода

Пусть имеется плоский измерительный контур, расположенный в плоскости (рис.4.10), а вдоль оси перемещается магнитный диполь с моментом

.

Магнитный поток, пронизывающий замкнутый контур с площадью

.

Используя связь индукции магнитного поля с векторным потенциалом в виде и теорему Стокса получим

,

где .

Рис.4.10

Векторный потенциал магнитного диполя имеет вид [17]

,

где .

Подставляя в получим

.

В координатной форме с учетом векторно-скалярного произведения

,

имеем

.

Для исключения зависимости от проинтегрируем в бесконечных пределах

.

После взятия интегралов с учетом

, ,

из получим:

.

Из видно, что если измерительный контур лежит в плоскости , то интегралы по обращаются в ноль, и

.

Пусть мы имеем прямоугольный контур, показанный на рис.4.11 Тогда при интегрировании против часовой стрелки получим

.

Отметим, что для любой другой формы плоского контура, целиком лежащего в плоскости значение контурного интеграла будет ; если путь интегрирования по лежит вне контура , то последний интеграл равен нулю.

Таким образом, принимает вид

.

Рис.4.11

Из непосредственно следует и метод измерения магнитного момента.

В работе [26] получено более общее соотношение. Если след всего тела на плоскости контура с числом витков лежит во внутренней области , то

.

Рис.4.11

4.7.3.Определение магнитного потока через произвольный кусочно-линейный контур

Если контур аппроксимирован прямолинейными литейными отрезками, при этом -начало го отрезка, а -конец го отрезка (рис.4.12), то из имеем

.

Учитывая, что , получим

,

Рис.4.12

где

; ;

;

;

;

;

;

.

.

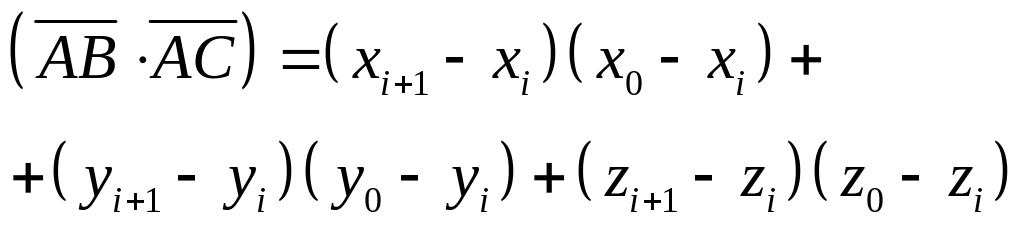Другой способ вычисления магнитного потока через произвольный контур основан на теореме о потокосцеплениях [27]

,

где -потокосцепление контура с источником магнитного поля, - индукция магнитного поля, созданного контуром с током в точке элемента источника (влияние намагниченности тела не учитывается), -магнитный момент элементарного объема .

Если в пределах объема , как намагниченность , так и индукция постоянны, то

.

Еще более простой вид для потокосцепления получаем, если устремить

,

где - магнитный момент дипольного источника, а остальные обозначения те же, что и в .

Если петлевой контур аппроксимирован прямолинейными отрезками, то принимает вид:

,

где

;

;

;

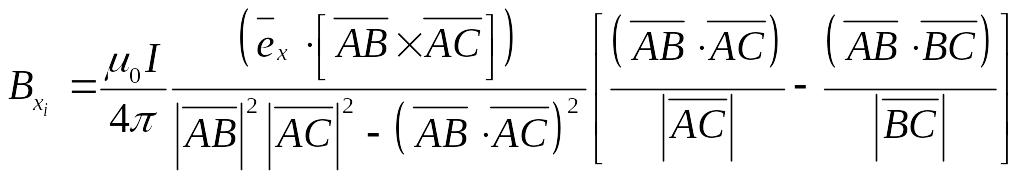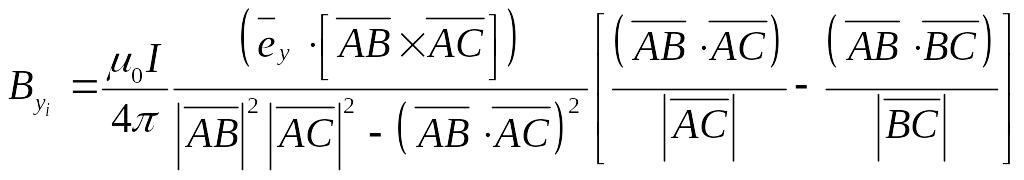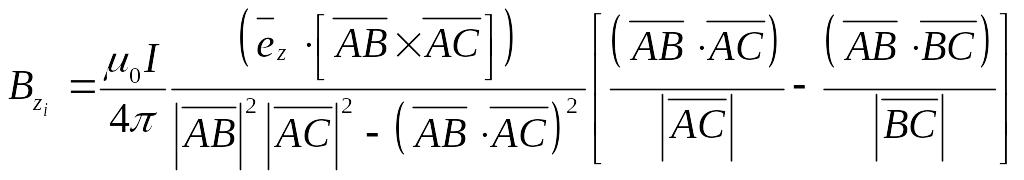Остальные обозначения те же, что и в .