
- •4. Замечательные пределы.
- •2 Замечательный предел.
- •5. Непрерывные функции и их свойства. Точка разрыва функций и их классификация.
- •6. Производная от функции. Дифференцируемость функции. Дифференциал.
- •7 Теорема Ферма.
- •9 Возрастание и убывание функции. Экстремумы функции. Связь с первой и второй производной
- •17 Свойства определённого интеграла.
- •11 Асимптоты графика функции.
- •12 Первообразная и её свойства. Неопределённый интеграл и его свойства. Таблица интегралов.
- •13 Способ подстановки в неопределённом интеграле. Интегрирование по частям в неопределённом интеграле
- •14 Интегрирование выражений, содержащих квадратный трёхчлен.
- •15 Интегрирование рациональных дробей.
- •16 Задача о вычислении площади криволинейной трапеции. Определённый интеграл
- •18 Теорема Барроу. Формула Ньютона-Лейбница.
- •19 Вычисление определённого интеграла подстановкой и по частям.
- •20 Несобственные интегралы.
- •31 Степенные ряды.
16 Задача о вычислении площади криволинейной трапеции. Определённый интеграл
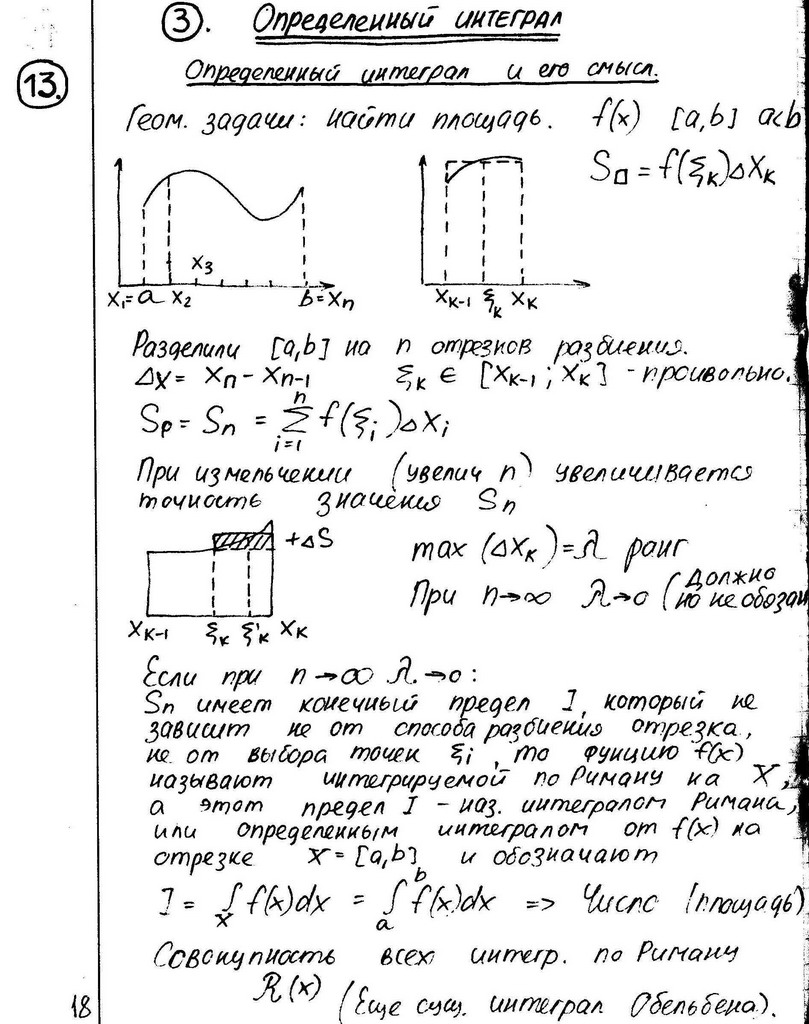
Пусть
на отрезке [a,b]задана
неотриц ф-я у=ф от х.Требуется найти
площадь криволин трапеции,ограниченной
прямой у=ф от х,прямыми х=а,х= b,и
осью абсцисс у=0
Нарисуем
ломаную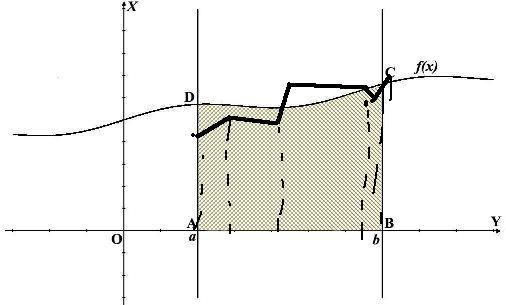
Фигура под ломан сост из трапеций.поскольку ломан наход близко к кривой то можно составить приблизит-е рав-во Sприблизит.равно Sл
Пусть
f(x) определена на [a;b]. Разобьём [a;b]на
части с несколькими произвольными
точками a = x0 < x1 < x2 < xn = b Тогда говорят,
что произведено разбиение R отрезка
[a;b] Далее выберем произв. точку![]() , i = 0, Определённым интегралом от функции
f(x) на отрезке [a;b]называется предел
интегральных сумм ΘR при
, i = 0, Определённым интегралом от функции
f(x) на отрезке [a;b]называется предел
интегральных сумм ΘR при
![]() ,
если он существует независимо от
разбиения R и выбора точек ξi, т.е
,
если он существует независимо от
разбиения R и выбора точек ξi, т.е![]() .
(1) Если существует (1), то функция f(x)
называется интегрируемой на [a;b] –
определение интеграла по Риману.
.
(1) Если существует (1), то функция f(x)
называется интегрируемой на [a;b] –
определение интеграла по Риману.
Пусть
ф от х непрерывна на отвезке а,б . Тогда
на этом отрезке существует неопред
интеграл
![]() и
имеет место формула
и
имеет место формула
![]()
![]()
![]()
18 Теорема Барроу. Формула Ньютона-Лейбница.
Пусть функция у = ƒ(х) интегрируема на отрезке [а; b].
Теорема
37.1. Если функция у = ƒ(х) непрерывна на
отрезке [а; b] и F(x) — какая-либо ее
первообразная на [а; b] (F'(x) = ƒ(х)), то имеет
место формула![]()
Разобьем отрезок [а;b] точками а = x0, x1,..., b = xn (x0 < x1 < ...< хn) на n частичных отрезков [x0;x1], [x1;x2],..., [xn-1;xn], как это показано на рис. 169.
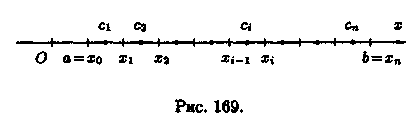
Рассмотрим тождество
![]()
Преобразуем каждую разность в скобках по формуле Лагранжа ƒ(b)-ƒ(а) = ƒ'(с)*(b-а).
Получим![]()
т.
е.![]()
где ci есть некоторая точка интервала (xi-1; xi). Так как функция у = ƒ(х) непрерывна на [а; b], то она интегрируема на [а; b]. Поэтому существует предел интегральной суммы, равный определенному интегралу от ƒ (х) на [а ;b].
Переходя
в равенстве (37.2) к пределу при λ = max ∆xi→0,
получаем![]()
![]()
Равенство
(37.1) называется формулой Ньютона-Лейбница.
Если ввести обозначение F(b)- F(a) = F(x)|ab ,
то формулу Ньютона-Лейбница (37.1) можно
переписать так:![]()
Формула Ньютона-Лейбница дает удобный способ вычисления определенного интеграла. Чтобы вычислить определенный интеграл от непрерывной функции ƒ (х) на отрезке [а; b], надо найти ее первообразную функцию F(x) и взять разность F(b)- F(a) значений этой первообразной на концах отрезка [a;b].
Теорема (Барроу):
Пусть![]() и непрерывна в
и непрерывна в![]() . ТогдаF
дифференцируема в этой точке и её
производная равна
. ТогдаF
дифференцируема в этой точке и её
производная равна![]() .
.
Доказательство:
Приращение
![]()
![]() при
при![]() в силу непрерывности в точке
в силу непрерывности в точке![]() выполняется
выполняется
![]()
Рассмотрим![]() .По
первому утверждению получаем
.По
первому утверждению получаем
![]()
Устремляя
![]() ,
получаем
,
получаем
![]()
Важное следствие
Утверждение:Пустьf
— непрерывна на![]() . Тогда на этом отрезке у неё существует
неопределённый интеграл.
. Тогда на этом отрезке у неё существует
неопределённый интеграл.![]()
В
силу непрерывности функции на отрезке
и теоремы Барроу
![]() — одна из первообразных.
— одна из первообразных.
Значит, неопределённый интеграл существует.
19 Вычисление определённого интеграла подстановкой и по частям.
Замена переменных в определенном интеграле.
Пусть
функция y
= f(x)
определена и непрерывна на отрезке [a;
b].
Множество [a;
b]
является областью значений некоторой
функции x
= g(z),
которая определена на интервале
![]() и имеет на нем непрерывную производную,
причем
и имеет на нем непрерывную производную,
причем
![]() и
и
![]() ,
тогда
,
тогда![]() .
.
Этой
формулой удобно пользоваться в тех
случаях, когда нам требуется вычислить
интеграл![]() , причем неопределенный интеграл
, причем неопределенный интеграл
![]() мы бы искали методом подстановки.
мы бы искали методом подстановки.
Интегрирование по частям в определенном интеграле.
Пусть
на отрезке [a; b] определены и непрерывны
функции u(x) и v(x) вместе со своими
производными первого порядка и функция
![]() – интегрируема, тогда на этом отрезке
интегрируема функция и справедливо
равенство
– интегрируема, тогда на этом отрезке
интегрируема функция и справедливо
равенство![]() .
.
Этой формулой удобно пользоваться в тех случаях, когда нам требуется вычислить интеграл , причем неопределенный интеграл мы бы искали интегрированием по частям.
