
- •1 Вопрос
- •2 Операции над множествами Бинарные операции
- •3 Интуитивное описание
- •Теоретико-множественное определение
- •Свойства
- •2 Вопрос
- •3 Вопрос
- •1.Определение
- •Ограниченные и неограниченные последовательности
- •4 Вопрос
- •1 Первый замечательный предел
- •2 Второй замечательный предел
- •5 Вопрос
- •3 Бесконечно малые
- •6 Вопрос
- •7 Вопрос
- •8 Вопрос
- •9 Вопрос
- •10 Вопрос
- •11 Вопрос
- •12 Вопрос
- •Точки разрыва. Классификация
- •13 Вопрос
- •14 Вопрос
- •15 Вопрос
14 Вопрос
Понятие дифференцируемости, необходимое условие(непрерывность)
1
Функция y=f(x) называется дифференцируемой в некоторой точке x0, если она имеет в этой точке определенную производную, т.е. если предел отношения существует и конечен.
Если функция дифференцируема в каждой точке некоторого отрезка [а; b] или интервала (а; b), то говорят, что она дифференцируема на отрезке [а; b] или соответственно в интервале (а; b).
Справедлива следующая теорема, устанавливающая связь между дифференцируемыми и непрерывными функциями.
2
Теорема. Если функция y=f(x) дифференцируема в некоторой точке x0, то она в этой точке непрерывна.
Таким образом,из дифференцируемости функции следует ее непрерывность.
Доказательство.
Если
![]() ,
то
,
то
![]() ,
,
где α бесконечно малая величина, т.е. величина, стремящаяся к нулю при Δx→0. Но тогда
Δy=f '(x0) Δx+αΔx=> Δy→0 при Δx→0, т.е f(x) – f(x0)→0 при x→x0, а это и означает, что функция f(x) непрерывна в точке x0. Что и требовалось доказать.
Таким образом, в точках разрыва функция не может иметь производной. Обратное утверждение неверно: существуют непрерывные функции, которые в некоторых точках не являются дифференцируемыми (т.е. не имеют в этих точках производной).
Р ассмотрим
на рисунке точки а,
b, c.
ассмотрим
на рисунке точки а,
b, c.
В точке a при Δx→0 отношение не имеет предела (т.к. односторонние пределы различны при Δx→0–0 и Δx→0+0). В точке A графика нет определенной касательной, но есть две различные односторонние касательные с угловыми коэффициентами к1 и к2. Такой тип точек называют угловыми точками.
В
точке b
при Δx→0
отношение
является
знакопостоянной бесконечно большой
величиной
![]() .
Функция имеет бесконечную производную.
В этой точке график имеет вертикальную
касательную. Тип точки – "точка
перегиба" cвертикальной касательной.
.
Функция имеет бесконечную производную.
В этой точке график имеет вертикальную
касательную. Тип точки – "точка
перегиба" cвертикальной касательной.
В точке c односторонние производные являются бесконечно большими величинами разных знаков. В этой точке график имеет две слившиесявертикальные касательные. Тип – "точка возврата" с вертикальной касательной – частный случай угловой точки.
15 Вопрос
Критерий, правила, таблица
1
Применяя общий способ нахождения производной с помощью предела можно получить простейшие формулы дифференцирования. Пусть u=u(x),v=v(x) – две дифференцируемые функции от переменной x.

 (справедлива
для любого конечного числа слагаемых).
(справедлива
для любого конечного числа слагаемых).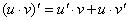 .
.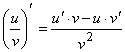 .
.
а)
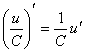 .
.
б)
 .
.
Доказательство формулы 3.
Пусть y = u(x) + v(x). Для значения аргумента x+Δx имеем y(x+Δx)=u(x+Δx) + v(x+Δx).
Тогда
Δy=y(x+Δx) – y(x) = u(x+Δx) + v(x+Δx) – u(x) – v(x) = Δu +Δv.
Следовательно,
![]() .
.
Доказательство формулы 4.
Пусть y=u(x)·v(x). Тогда y(x+Δx)=u(x+Δx)·v(x+Δx), поэтому
Δy=u(x+Δx)·v(x+Δx) – u(x)·v(x).
Заметим, что поскольку каждая из функций u и v дифференцируема в точке x, то они непрерывны в этой точке, а значит u(x+Δx)→u(x), v(x+Δx)→v(x), при Δx→0.
Поэтому можем записать
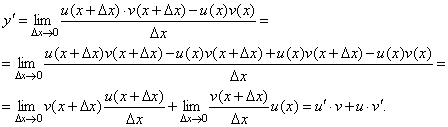
На основании этого свойства можно получить правило дифференцирования произведения любого числа функций.
Пусть, например, y=u·v·w. Тогда,
y ' = u '·(v·w) + u·(v ·w) ' = u '·v·w + u·(v '·w +v·w ') = u '·v·w + u·v '·w + u·v·w '.
Доказательство формулы 5.
Пусть
![]() .
Тогда
.
Тогда

При доказательстве воспользовались тем, что v(x+Δx)→v(x) при Δx→0.
2
 .
.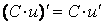 .
..
.
.
а) .
б) .
 .
. .
.
![]() .
.

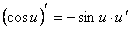 .
. .
. .
. .
.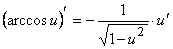 .
. .
. .
. .
.
