
- •1 Вопрос
- •2 Операции над множествами Бинарные операции
- •3 Интуитивное описание
- •Теоретико-множественное определение
- •Свойства
- •2 Вопрос
- •3 Вопрос
- •1.Определение
- •Ограниченные и неограниченные последовательности
- •4 Вопрос
- •1 Первый замечательный предел
- •2 Второй замечательный предел
- •5 Вопрос
- •3 Бесконечно малые
- •6 Вопрос
- •7 Вопрос
- •8 Вопрос
- •9 Вопрос
- •10 Вопрос
- •11 Вопрос
- •12 Вопрос
- •Точки разрыва. Классификация
- •13 Вопрос
- •14 Вопрос
- •15 Вопрос
10 Вопрос
Сравнение бесконечно малых, таблица
11 Вопрос
Бесконечно большие, связь с бесконечно малыми
Теорема 1. Если функция f(x) является бесконечно большой при x→a, то функция 1/f(x) является бесконечно малой при x→a.
Доказательство.
Возьмем произвольное число ε>0
и покажем, что при некотором δ>0
(зависящим от ε) при всех x,
для которых |x
– a|<δ,
выполняется неравенство
![]() ,
а это и будет означать, что 1/f(x)
–
бесконечно малая функция. Действительно,
так как f(x)
– бесконечно большая функция при x→a,
то найдется δ>0
такое, что как только |x
– a|<δ,
так |f(x)|>1/
ε. Но тогда для тех же x
.
,
а это и будет означать, что 1/f(x)
–
бесконечно малая функция. Действительно,
так как f(x)
– бесконечно большая функция при x→a,
то найдется δ>0
такое, что как только |x
– a|<δ,
так |f(x)|>1/
ε. Но тогда для тех же x
.
Примеры.
Ясно, что при x→+∞ функция y=x2+1 является бесконечно большой. Но тогда согласно сформулированной выше теореме функция
 –
бесконечно малая при x→+∞,
т.е.
–
бесконечно малая при x→+∞,
т.е.
 .
.
 .
.
Можно доказать и обратную теорему.
Теорема 2. Если функция f(x) - бесконечно малая при x→a (или x→∞) и не обращается в нуль, то y=1/f(x) является бесконечно большой функцией.
Доказательство теоремы проведите самостоятельно.
Примеры.
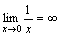 .
.
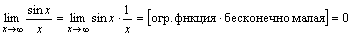 .
.
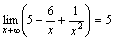 ,
так как функции
,
так как функции
 и
и
 -
бесконечно малые при x→+∞,
то
-
бесконечно малые при x→+∞,
то
 ,
как сумма бесконечно малых функций
есть функция бесконечно малая. Функция
же
,
как сумма бесконечно малых функций
есть функция бесконечно малая. Функция
же
 является
суммой постоянного числа и бесконечно
малой функции. Следовательно, по теореме
1 для бесконечно малых функций получаем
нужное равенство.
является
суммой постоянного числа и бесконечно
малой функции. Следовательно, по теореме
1 для бесконечно малых функций получаем
нужное равенство.
Таким образом, простейшие свойства бесконечно малых и бесконечно больших функций можно записать с помощью следующих условных соотношений: A≠ 0
![]() .
.
12 Вопрос
Односторонние пределы, классификация точек разрыва
1
До сих пор мы рассматривали определение предела функции, когда x→a произвольным образом, т.е. предел функции не зависел от того, как располагалось x по отношению к a, слева или справа от a. Однако, довольно часто можно встретить функции, которые не имеют предела при этом условии, но они имеют предел, если x→a, оставаясь с одной стороны от а, слева или справа (см. рис.). Поэтому вводят понятия односторонних пределов.
Если
f(x)
стремится
к пределу b
при x
стремящемся к некоторому числу a
так, что xпринимает
только значения, меньшие a,
то пишут
![]() и
называют bпределом
функции f(x) в точке a слева.
и
называют bпределом
функции f(x) в точке a слева.
Таким
образом, число b
называется пределом функции y=f(x)
при x→aслева,
если каково бы ни было положительное
число ε, найдется такое число δ (меньшее
a),
что для всех
![]() выполняется
неравенство
выполняется
неравенство
![]() .
.
Аналогично,
если x→a
и принимает значения большие a,
то пишут
![]() и
называют b
пределом функции в точке а
справа. Т.е. число b
называется пределом
функции y=f(x) при x→a справа,
если каково бы ни было положительное
число ε, найдется такое число δ (большее
а),
что для всех
и
называют b
пределом функции в точке а
справа. Т.е. число b
называется пределом
функции y=f(x) при x→a справа,
если каково бы ни было положительное
число ε, найдется такое число δ (большее
а),
что для всех
![]() выполняется
неравенство
.
выполняется
неравенство
.
Заметим, что если пределы слева и справа в точке a для функции f(x) не совпадают, то функция не имеет предела (двустороннего) в точке а.

2
Точки разрыва. Классификация
Е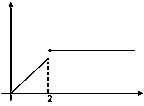
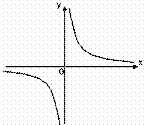 сли
рассмотреть график функции
сли
рассмотреть график функции
![]() в
окрестности точки x=
0 (см. рис. справа), то ясно видно, что он
как бы “разрывается” на отдельные
кривые. Аналогично можно рассмотреть
функцию, изображенную на рисунке слева
в окрестности точки 2. Говорят, что во
всех указанных точках соответствующие
функции становятся разрывными.
в
окрестности точки x=
0 (см. рис. справа), то ясно видно, что он
как бы “разрывается” на отдельные
кривые. Аналогично можно рассмотреть
функцию, изображенную на рисунке слева
в окрестности точки 2. Говорят, что во
всех указанных точках соответствующие
функции становятся разрывными.
Точка
![]() называется
точкой
разрыва функции
y = f(x),
если она принадлежит области определения
функции или её границе и не является
точкой непрерывности.
называется
точкой
разрыва функции
y = f(x),
если она принадлежит области определения
функции или её границе и не является
точкой непрерывности.
В
этом случае говорят, что при x=
x0
функция разрывна. Это может произойти,
если в точке x0
функция не определена или не существует
предел
![]() ,
или если предел существует, но
,
или если предел существует, но
![]() .
.
