Агрегатів на електростанціях

Для гідравлічних турбін таким регулюючим органом служить направляючий апарат, відкриття якого як координата управління позначається .

Навантаження в місцях споживання змінюється безперервно. Найменший період зміни — доба. Зафіксовані через визначений інтервал часу (зазвичай година) або безперервно значення навантаження складають так званий добовий графік навантаження даного споживача або вузла споживання. Добовий графік характеризується максимальним (піковим), мінімальним і середнім навантаженнями. Чим більше відхилення екстремальних навантажень від середньої, тим менше ущільнений графік, тим більший діапазон зміни навантажень агрегатів, регулюючих потужність. З окремих графіків навантаження вузлів (районів) споживання складаються відповідні графіки навантаження ЕЕС, ОЕС і ЄЕС. Зміна навантаження у вузлах споживання має в основному плановий (детермінований) характер, але завжди виникають непланові, випадкові зміни навантаження навіть при найдосконалішому прогнозуванні. Мають місце і аварійні зміни розвиваючої, переданої і реалізованої потужності. Для підтримки системного балансу активної потужності необхідне регулювання частоти обертання агрегатів на відповідних ЕС.

Виробництво, розподіл і реалізація електричної енергії повинні проводитись при мінімальних трудових затратах, тому режим роботи ЕЕС повинен бути в цьому плані оптимальним. На оптимальність режиму ЕЕС істотно впливає розподіл навантажень між джерелами енергії, тобто між окремими парогенераторами, турбоагрегатами ЕС і між ЕС, що входять в ЕЕС, а також потокорозподіл в мережах живлення.

По мірі зростання ЕЕС, створення ОЕС і ЄЕС підвищується стабільність частоти, оскільки частка окремих випадково і дискретно змінюваних споживачів знижується. Проте навіть невелике відхилення частоти призводить до великих абсолютних змін потужності, що порушує оптимальність режиму роботи окремих ЕС. В цих умовах велику роль відіграє регулювання потужності агрегатів окремих ЕС, що забезпечує їх оптимальний режим і потокорозподіл в мережах, де можуть виникати недопустимі перевантаження ліній високої напруги.

Все сказане визначає необхідність автоматичного регулювання частоти і потужності агрегатів для забезпечення стабільності частоти в ЄЕС, ОЕС і ЄЕС, оптимальності і надійності їхньої роботи в різних режимах. З цією метою в окремих ЄЕС, об'єднаннях і Єдиній енергетичній системі країни створюється автоматична система регулювання частоти і потужності (АСРЧ і П), побудована на ієрархічному принципі і є підсистемою АСУ галузі виробництва, розподілу і використання електричної енергії. Для вивчення принципів формування АСРЧ і П необхідно розглянути елементи її реалізації для агрегатів ЕС, ЄЕС, ОЕС і ЄЕС.

3.2 Турбіна як об'єкт регулювання частоти і потужності

Для того щоб з'ясувати особливості турбіни як об'єкту регулювання, необхідно оцінити її здатність нести навантаження при різних значеннях частоти обертання в сталих режимах і визначити поведінку турбіни в перехідному процесі при тих або інших обуреннях. Особливості турбіни можуть бути визначені з основного диференціального рівняння руху ротора агрегату, записаного для моментів на валу агрегату:

(3.1)

де J — момент інерції ротора агрегату; M_T— рушійний момент на валу турбіни; М_Г — момент опору на валу генератора, згідно якому сталий режим має місце при М_Т=М_Г, а перехідні процеси визначаються динамічним моментом М_Д=М_Т—М_Г.

Для оцінки здатності турбіни нести навантаження при різних значеннях частоти обертання звичайно використовуються статичні характеристики турбіни — M_T (ω) і генератора М_Г (ω). Статичні характеристики турбін можуть бути отримані з рівнянь їх потужності по співвідношенню М_Т=Р_Т /ω

Для парової турбіни:

де А_П— числовий коефіцієнт, який залежний від прийнятих одиниць вимірювання; D —часова витрата пари; H_o— тепловий перепад; η_o — тепловий ККД парової турбіни.

Для гідравлічної турбіни:

,

де А_Г - числовий коефіцієнт, який залежить від прийнятих одиниць вимірювання; Q - витрата води; H - діючий тиск;

η - ККД гідротурбіни.

Оскільки момент турбіни залежить від витрати енергоносія, його потенційної енергії і ККД, то звичайно статичні характеристики в координатах M_T, ω для різних значень положення регулюючого органу представляють сімейством кривих, приблизний вигляд яких показано на рис. 3.2

Рисунок 3.2 - Моментні характеристики турбіни M_T (ω) і генератора М_Г(ω).

Статичні характеристики генератора визначаються статичними характеристиками навантаження, розглянутими вище (див. гл. 5). Ці характеристики генератора в координатах M_T, ω для різних значень навантаження при номінальній частоті представляються сімейством кривих, зразковий вид яких також показаний на рис. 3.2.

В сталому режимі роботи агрегату, коли М_Т=М_Г, динамічний момент рівний нулю, рівно нулю і прискорення; агрегат має постійну частоту обертання. На рис. 3.2 точка а відповідає деякому сталому режиму при постійному значенні ω_а.

Якщо навантаження в будь-який момент часу зміниться, наприклад зменшиться, то відбудеться перехід із статичної характеристики М_Г,1 на характеристику М_Г,₂ при незмінній кількості пари, яка подається в турбіну. Виникає динамічний момент М_Д і прискорення. Почнеться перехідний процес (динамічний перехід), в результаті якого наступить новий сталий режим, який відповідає точці b, при якому М_Г,2 стане рівним М_Т,1, а кутова частота обертання збільшиться до значення ω_b· Властивість турбін переходити із одного сталого режиму в інший при подачі незмінної кількості енергоносія називається самовирівнювання або саморегулювання. Однак, при зміні режиму агрегату від холостого ходу до номінального відхилення ω і ККД турбіни будуть значними.

Для збереження частоти обертання на попередньому рівні слід змінити кількість пари, яка подається в турбіну, що призведе до переходу на характеристику М_Т,2 і повернення частоти обертання до значення ω_а · Отже, для підтримки величини ω при змінах навантаження слід автоматично впливати на регулюючі органи турбіни, для відповідної зміни кількості енергоносія. Цю роль виконують автоматичні регулятори частоти обертання (АРЧО), що є невід'ємною частиною парових і гідравлічних турбін.

Для досліджень законів регулювання частоти і потужності звичайно використовується лінійна теорія автоматичного регулювання (див. гл. 6), де розглядаються процеси при малих обуреннях, що виникають в лінійній моделі агрегату. Для отримання такої лінійної моделі в загальному випадку нелінійна залежність М_Т(ω, D) і М_Г (ω) розкладається в ряд Тейлора по приростах координат ω і D і використовується лінійна частина цього розкладу. Лінеаризоване диференціальне рівняння запишеться у вигляді

, (3.2)

де ω_о — кутова частота обертання в початковому режимі; D_о - витрата пари через турбіну в початковому режимі.

В теорії автоматичного регулювання незалежні змінні (координати) і їх прирости виражаються у відносних безрозмірних одиницях. В літературі по регулюванню турбін безрозмірні координати позначаються буквами грецького алфавіту. За базисні звичайно приймаються їх номінальні значення ω_ном , D_ном і координати визначаються як

Вираз (3.2) при безрозмірних координатах має вигляд:

(3. 2а)

Проте права і ліва частини рівняння мають розмірність моменту і для переходу до безрозмірного диференціального рівняння вибирається базисне значення моменту, в якості якого можуть бути прийняті _ном, або D_ном або номінальний момент М_Т,ном. Від прийнятого базисного моменту залежить вид диференціального рівняння руху і відповідної передавальної функції турбіни, як типової ланки . Так, якщо за базисний момент приймається _ном , то диференціальне рівняння для лінійної моделі агрегату записується у вигляді

де - постійна часу інерції агрегату; — коефіцієнт передачі.

Передавальна функція має вигляд:

,

де —зображення відповідних координат.

При використовуванні в якості базисного моменту М_Т,ном лінійне диференціальне рівняння руху парової турбіни можна записати у вигляді

де — постійна часу інерції агрегату, яка чисельно рівна часу розгону агрегату, з, від = 0 до _ном при постійному номінальному моменті; -коефіцієнт самовирівнювання агрегату.

Передавальна функція турбіни

. (3.3)

Як видно з приведених виразів для передавальної функції, турбіна може бути представлена як інерційна ланка першого порядку. Проте часто самовирівнювання турбіни не враховується (коефіцієнт  приймається рівним нулю), турбіна представляється інтегруючою ланкою з диференціальним рівнянням вигляду

і передавальною функцією вигляду

(3.4)

Раніше приведені співвідношення записані в термінах і позначеннях, використовуваних в технічній літературі по конструюванню турбін. В літературі, присвяченій дослідженню електромеханічних перехідних процесів, використовується дещо інша термінологія і позначення. Щоб читач міг успішно орієнтуватися в різних літературних джерелах, ті або інші співвідношення будуть даватися у відповідних термінах і позначеннях.

Наведений приклад лінійного моделювання турбіни як об'єкту регулювання виявляв взаємозв'язок між зміною положення регулюючого органу, як вхідної координати і зміною частоти обертання, як координати виходу. Проте для різних режимів роботи турбоагрегату, його лінійні моделі відрізняються одна від одної, оскільки повинні враховуватися різні чинники, що впливають на перехідні процеси в ньому.

Нижче розглядаються основні режими роботи агрегатів і відповідні лінійні моделі.

Режим холостого ходу. З погляду стійкості системи регулювання частоти обертання агрегату цей режим є найважчим, оскільки відсутній синхронізуючий момент в гeнераторі, сприяючий збереженню стійкості.

При дослідженнях режиму холостого ходу модель агрегату представляється інтегруючою ланкою з постійної часу інерції T_J, що враховує маси роторів турбіни, що обертаються і генератора. Вхідна і вихідна координати залишаються попередніми, ефект самовирівнювання турбіни не враховується, оскільки витрата енергоносія мала. Модель агрегату показана на рис. 3.3.

Режим роботи агрегату (групи агрегатів) на ізольоване навантаження або в автономній ЕЕС. При паралельній роботі групи агрегатів здійснюється заміна їх одним еквівалентним агрегатом. Модель агрегату розділяється на модель генератора і модель турбіни. Інертність мас роторів турбіни, що обертаються і генератора враховується в моделі генератора, яка представлена інтегруючою ланкою з постійною часу інерції T_J. Для врахування регулюючого ефекту навантаження, а іноді, і для врахування ефекту самовирівнювання, в турбіні вказана ланка охоплюється ланкою жорсткого від’ємного зворотного зв'язку з коефіцієнтом передачі, що враховує регулюючий ефект навантаження або регулюючий ефект навантаження і самовирівнювання турбіни .

(p)

(p)

1/T_jp

Рисунок 3.3 - Модель агрегату в режимі холостого ходу

Оскільки вихідною координатою зворотного зв'язку є потужність, то вхідною координатою інтегруючої ланки, теж повинна бути потужність. Зміна вхідної координати дозволяє реалізувати обурення на вході моделі як зміна навантаження генератора . Передавальна функція еквівалентного генератора записується у вигляді

(3.5)

де - зображення приросту кутової частоти обертання; - зображення приросту потужності турбіни; T_J - постійна часу інерції, обчислена з врахуванням переходу на нову вхідну координату.

Модель агрегату в режимі навантаження показана на рис. 3.4. Оскільки при регулюванні агрегату кількість енергоносія при зміні навантаження міняється, виникає необхідність моделювати взаємозв'язок між положенням регулюючого органу і потужністю, що розвивається на валу турбіни, і враховувати інертність енергоносія (пари або води) при зміні положення регулюючого органу, що і здійснюється в моделі турбіни.

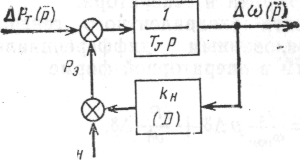
Рисунок 3.4- Модель генератора в режимі автономного навантаження

Для парових турбін без проміжного перегріву в моделі враховується лише інертність парового об'єму в паропроводі від дросельного клапана до входу в циліндр високого тиску (ЦВТ). Турбіна моделюється інерційною ланкою з постійною часу, рівній часу спорожнення паропроводу Т_П. Передавальна функція турбіни записується у вигляді

(3.6)

де —зображення приросту положення дросельного клапана.

Модель парової турбіни без проміжного перегріву показана на рис. 3.5. Модель турбоагрегату складається з моделі турбіни і моделі генератора.

Для парової турбіни з проміжним перегрівом пари в моделі враховується інерційна пара до входу в ЦВТ аналогічно турбіні без проміжногo перегріву. Крім того, враховується значна інерційність об'єму пари в пароперегрівачу.

Пароперегрівач моделюється інерційною ланкою з постійною часу його спорожнення Т_ПП.

Рисунок 3.5 - Модель парової турбіни без проміжного

перегріву пару

В ЦВТ турбін розвивається лише частина потужності турбіни (с=0,15...0,3), решта частини (1—с) розвивається в ЦСТ і ЦНТ.

Оскільки перегрітий пар проходить тільки через ЦСТ і ЦНТ, пароперегрівач має передавальну функцію виду

З врахуванням сказаного, передавальна функція турбіни з проміжним перегрівом записується у вигляді

(3.7)

Іноді вираз в дужках приводить до одного знаменника і моделюють турбіну з проміжним перегрівом двома послідовно включеними ланками

Модель турбіни з проміжним перегрівом показанa на рис. 3.6.

Для гідравлічної турбіни інертність водяного потоку проявляється в так званому «гідравлічному ударі», що відбувається у водопідвідних спорудах і в проточній частині турбіни. Якщо відбувається стрибкоподібна зміна положення направляючого апарату турбіни а у бік закриття, як це, показано на рис. 3.7,а, то в результаті збільшення тиску води у водоводі і збільшення швидкості потоку води потужність, що розвивається турбіною в перехідному процесі, спочатку збільшується, а потім починає зменшуватися до нового встановленого значення, що відповідає новому положенню направляючого апарату.

.

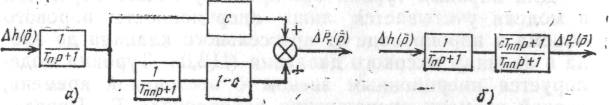
Рисунок 3.6 -Модель парової турбіни з проміжним перегрівом пари: а - перший варіант моделі;

б- другий варіант моделі

Явище гідравлічного удару описується алгебраїчними і диференціальними рівняннями, які зв'язують швидкість потоку води, напір, відкриття направляючого апарату і довжину водоводу. Спільне рішення цих рівнянь дозволяє визначити передавальну функцію гідравлічної турбіни у вигляді

Рисунок 3.7- Модель гідравлічної турбіни з врахуванням гідравлічного удару: а- явище гідравлічного удару; б - модель турбіни

(3.8)

де α_о — відкриття направляючого апарату в початковому режимі; Т_В — постійна часу водоводу, Т_В=Lυ_о/gH_о; H_о, υ_о — напір і швидкість руху води в початковому режимі; L — довжина водоводу; g — прискорення падаючої води.

Модель гідравлічної турбіни з врахуванням гідравлічного удару показана на рис. 3.7,б.

Режим роботи агрегату в потужній ЕЕС. В цьому режимі регулювання потужності агрегату відбувається при постійності частоти, тому модель еквівалентного агрегату повинна відображати зміну потужності еквівалентного генератора під впливом зміни кута вектора ЕРС генератора δ по відношенню до вектора напруги в опорній точці електроенергетичної системи.

Дослідження перехідних процесів звичайно проводиться при роботі еквівалентного агрегату через лінію високої напруги на шини нескінченної потужності - в одномашинній схемі або в двомашинній схемі. При моделюванні використовується лінеаризоване диференціальне рівняння, яке визначає прискорення при зміні потужності,

(3.9)

де T_J,ек — еквівалентна постійна часу інерції мас, що обертаються, в ЕЕС; ∆Р_Т; ∆Р_Т — прирости потужностей еквівалентних турбін і генератора.

Приріст потужності еквівалентного генератора визначається лінеаризованим диференціальним рівнянням, записаним в операторній формі

де перший член правої частини враховує появу потужності, обумовленої асинхронним моментом, а другий - зміну синхронної потужності еквівалентного генератора.

Приріст потужності еквівалентної турбіни визначається з рівняння (3.9), записаного в операторній формі

. (3.10)

Передавальна функція еквівалентного агрегату в даному режимі записується у вигляді

(3.11)

Приведені співвідношення для моделей агрегатів в різних режимах роботи дозволяють проводити дослідження перехідних процесів в АСРЧ і П.