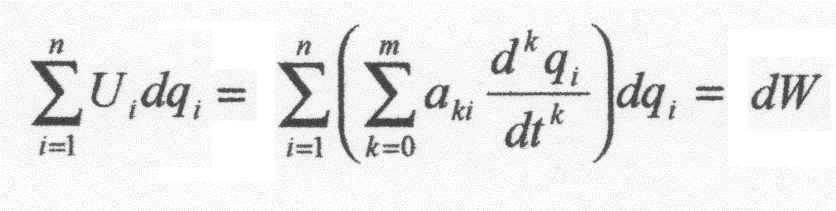- •6. Работа, мощность, энергия
- •7. Кинетическая и потенциальная энергия
- •Формы записи закона сохранения энергии в классической физике
- •Расширенная форма записи закона сохранения энергии
- •9. Закон сохранения импульса.
- •11. Удар абсолютно упругих и неупругих тел
- •12. Момент импульса
- •14. Момент инерции
- •14.1 Теорема Штейнера
- •15. Кинетическая энергия вращения
- •16. Момент импульса. Тензор инерции.
- •17. Свободные оси. Гироскоп
- •18. Деформация твердого тела
- •19. Неинерциальные системы отсчета и силы инерции
Формы записи закона сохранения энергии в классической физике
В популярном справочнике по физике (Б.Яворский и А.Детлаф, 1990) закон сохранения энергии имеет следующую форму записи в виде обобщенного уравнения состояния замкнутой термодинамической системы: W = Wk + Wp + U , (1) где W – полная энергия системы; Wk − кинетическая энергия системы в целом; Wp − потенциальная энергия системы в целом; U – внутренняя энергия системы. Смысл слов “в целом” состоит в том, что значения кинетической энергии и потенциальной энергии во всех формах движения системы просуммированы друг с другом. Закон сохранения энергии можно распространить на незамкнутые системы, если принять во внимание условие приращений. Это условие требует записывать при систематизации физических величин определяющие уравнения, к которым относится и уравнение состояния, не в абсолютных значениях величин, а в их приращениях. На основании уравнения (1) приращение энергии системы с учетом соблюдения принципа причинности можно записать как сумму приращений видов энергии: Σi (dWk)i + Σi (dWp)i + Σi (dU)i = dW . (2) Уравнения (1) и (2) указывают на то, что внутри системы энергия может переходить из одного вида энергии в другой (из кинетической энергии в потенциальную) и наоборот при неизменности внутренней энергии, а также переходить из внутренней энергии в кинетическую и потенциальную энергии и наоборот. Форма записи (1) не учитывает возможность перехода энергии из одной формы движения в другую, то есть не учитывает классификацию энергии по формам и видам. Недостатком формы записи (1) является также ее приемлемость лишь для замкнутой системы. Обратим также внимание на то, что в уравнениях (1) и (2) не отражена энергия диссипации, являющаяся одним из видов любой формы энергии. Так как идеализированные системы, в которых не учитывается явление диссипации, являются консервативными системами, то уравнения (1) и (2) приемлемы лишь для консервативных систем. Более объективной формой записи закона сохранения энергии является уравнение состояния, приведенное, например, у В.Сычёва (1970):
|
( 3 ) |
где dqi − приращение координаты состояния системы. Запись уравнения состояния в форме (3), в отличие от записи в форме (1), учитывает возможность перехода энергии из одной формы в другую внутри системы, но не учитывает возможность перехода из одного вида энергии в другой внутри любой формы движения. Уравнение состояния в форме (3) может быть применено и как уравнение состояния для одной формы движения. Однако напоминаем, что форма записи уравнения состояния (3) противоречит принципу причинности, в ней следует переставить местами левую и правую части.
Расширенная форма записи закона сохранения энергии
В основу построения системы ЭСВП (И.Коган, 2004) положено суммирование как по формам энергии, так и по видам энергии. Для этой цели следует в уравнении (3) расшифровать каждое выражение в круглых скобках с помощью обобщенного уравнения динамики, приведенного на странице, посвященной переходному процессу в системе. И тогда уравнение состояния (3) после учета принципа причинности запишется в такой обобщенной форме:
|
( 4 ) |
где n − число форм движения (форм энергии) в системе; k − порядок производной по времени в уравнении динамики; m − число учитываемых видов энергии в форме энергии; аi − конструктивный параметр i-ой формы движения; Ui = (∂W/∂t)0 − динамическое воздействие на i-ую форму движения из уравнения (3). Закон сохранения энергии в форме записи (4) примечателен тем, что в нем сначала подсчитываются суммы в круглых скобках, то есть суммирование ведется сначала по видам энергии, а уж потом определяется общая сумма, где суммирование ведется по формам энергии. Это как раз и соответствует расположению форм и видов энергообмена на схеме, учитывающей классификацию форм и видов энергии, а также на схеме иерархии уровней систематизации физических величин. Для полного учета всех форм энергии в левую часть уравнения состояния (4) должна быть добавлена сумма приращений энергии, вызванных изменением состояния системы под влиянием разных форм физического поля. Тогда уравнение состояния примет такой обобщенный вид: Σi Ui dqi + Σj Uj dqj = dW , (5 ) где i – число форм движения; j – число форм физического поля. Уравнение (5) является наиболее полной формой записи закона сохранения энергии по сравнению с другими формами его записи в современной физике. Уравнения (4) и (5) отражают не только перенос энергии из системы в среду или из среды в систему, но и перенос энергии из одной формы движения в другую внутри системы, из энергии физического поля в энергию любой формы движения и наоборот. Поэтому эти уравнения и положены в основу закона сохранения энергии, полное название которого − закон сохранения и превращения энергии. Закон сохранения энергии в современной трактовке ничего не говорит о сохранении направления движения, так как энергия является скалярной величиной. Но на странице, посвященной энергии, показано, что энергия является векторной физической величиной. То есть закон сохранения энергии должен учитывать не только количество энергии, но и направление движения. Именно в таком качестве закон сохранения энергии отражает не только вечное существование материи, но и вечное ее движение.