5.5. Временное сигнальное кодирование

Большинство технических приемов кодирования аналоговых источников предназначены для кодирования речи и изображений. При сигнальном кодировании (СК) кодер источника представляет в цифрах временные характеристики сигнала источника. Изучим основные виды СК .

Импульсно-кодовая модуляция (ИКМ). Пусть - реализация сигнала источника, а - отсчет, взятый со скоростью стробирования , где - максимальная частота в спектре . В ИКМ каждый отсчет квантуется в один из уровней, где - число двоичных цифр для представления одного отсчета. Тогда скорость кодирования источника равна бит/с. Квантование математически опишем как , где - квантованное значение , и - ошибка квантования (аддитивный шум). Характеристика вход-выход равномерного квантователя показана на рис. 5.2.

Рис. 5.2. Характеристика вход-выход для равномерного квантователя

Нормируем на интервал возможных изменений , учитываемых при квантовании. Равномерный квантователь оптимален, если ФПВ , , где шаг квантования . Средний квадрат ошибки квантования (см. (5.2) при ), то есть дБ. Видно, что шум квантования уменьшается на 6 дБ на каждый используемый в квантователе бит. Например, -битовый квантователь вызывает мощность шума квантования в дБ.

Для многих источников, таких как речевые, характерно более частое появление сигналов, соответствующих малым по значению уровням, чем большим. Тогда равномерное квантование во всем динамическом диапазоне изменения сигнала не оптимально. Характеристики оптимального неравномерного квантователя обычно получают пропусканием сигнала через нелинейное устройство (компрессор), сжимающее динамический диапазон сигнала. Из-за нелинейности преобразования сигнала в компрессоре сжатие оказывается неравномерным в разных частях динамического диапазона сигнала. Сжатый сигнал поступает в равномерный квантователь. При восстановлении сигнала по квантованным значениям применяют экспандирование – преобразование амплитуды сигнала, обратное сжатию. Комбинированную пару компрессор-экспандер называют компандером.

Пример 5.5.1. Изучим логарифмический компрессор с амплитудной характеристикой вход-выход

где - амплитуда входа, - амплитуда выхода, - параметр, от значения которого зависят свойства характеристики квантователя. В случае квантования нет. Значение дает уменьшение мощности шума квантования относительно равномерного квантования приблизительно на дБ. При этом -битовый квантователь, применяемый вместе с логарифмическим компрессором, дает мощность шума квантования примерно дБ по сравнению с дБ при равномерном квантовании.

Дифференциальная импульсно-кодовая модуляция (ДИКМ). В ИКМ каждый отсчет кодируют независимо от других. У многих источников при стробировании сигнала со скоростью Найквиста или быстрее появляется значительная корреляция между отсчетами. То есть, изменение амплитуды сигнала между последовательными отсчетами в среднем относительно мало. Учет избыточности отсчетов требует более низкой битовой скорости кодирования на выходе источника.

Относительно простые решения получаются при кодировании разности между последовательными отсчетами, а не самих отсчетов. Разность между отсчетами сигнала по модулю обычно меньше значений самих отсчетов. Поэтому для отображения разностного сигнала нужно меньшее число бит. Суть общего подхода – в предсказании текущего значения отсчета на основе предыдущих отсчетов. Пусть - текущий отсчет источника, и - предсказанное значение (оценка) для , . Видно, что является линейной комбинацией отсчетов сигнала , взвешенной по коэффициентам предсказания . Значения определяются минимизацией некоторой функции-ошибки между и , например, - среднеквадратической ошибки путем нахождения математического ожидания . Для стационарного источника это дает систему нормальных уравнений (уравнений Юли-Волкера) относительно :

(5.7)

где - автокорреляционная функция последовательности отсчетов , и . Если заранее неизвестна, ее можно оценить по реализации отсчетов : , . Решение уравнений (5.7) лежит в основе линейного кодирования с предсказанием (см. п. 5.7).

Блок-схема практической системы ДИКМ показана на рис. 5.3 ((а) – кодер ДИКМ, (б) – декодер ДИКМ в приемнике). Предсказатель встроен в цепь обратной связи, охватывающей квантователь. Вход предсказателя обозначен . Он представляет сигнальный отсчет , видоизмененный процессом квантования, а выход квантователя . Разность является входом квантователя, а обозначает его выход. Величина квантованной ошибки предсказания кодируется последовательностью двоичных символов и передается через канал в пункт приема. Квантованная ошибка еще суммируется с предсказанной величиной , чтобы получить . В месте приема (см. рис. 5.3, б) есть такой же предсказатель, как и на передаче. Выход предсказателя суммируется с , чтобы получить . Сигнал служит входным воздействием для предсказателя и образует выходную последовательность. По ней с помощью фильтра НЧ восстанавливают сигнал . Применение обратной связи вокруг квантователя дает то, что ошибка в - это просто ошибка квантования: , и что здесь нет накопления предыдущей ошибки квантования при декодировании. Так как , квантованный отсчет отличается от входа ошибкой квантования независимо от применения предсказателя, и нет накопления ошибок квантования.

В системе ДИКМ (см. рис. 5.3) оценка (предсказанное значение) отсчета сигнала - линейная комбинация предыдущих значений , , то есть . Качество оценки можно улучшить, включая в нее линейно отфильтрованные последние значения квантованной ошибки. То есть, , где - коэффициенты фильтра для квантованной последовательности ошибок . Два ряда коэффициентов и выбирают так, чтобы минимизировать некоторую функцию ошибок, например, - среднеквадратичную ошибку.

Рис. 5.3 (а) Блок-схема кодера ДИКМ; (б) Декодер ДИКМ в приемнике

Пример 5.5.2. Дельта-модуляция (ДМ) - простейшая форма ДИКМ. В ней используется уровневый ( -битовый) квантователь в соединении с фиксированным предсказанием го порядка ( ):

. (5.8)

Так как , то с учетом (5.8) . То есть, оцененное (предсказанное) значение совпадает с предыдущим отсчетом , измененным шумом квантования . Разностное уравнение (5.8) определяет интегратор с входом . Поэтому эквивалентная схема предсказателя го порядка – интегратор с входом, равным квантованному сигналу ошибки. В общем случае интегратор масштабируется размером шага . Блок-схемы кодера и декодера ДМ показаны на рис. 5.4.

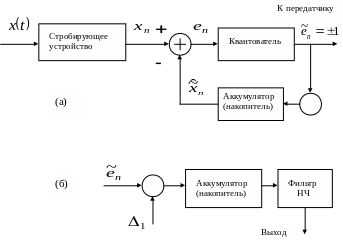
Фильтр НЧ

Рис. 5.4. (а) Блок-схема кодера ДМ; (б) Декодер ДМ в приемнике

Кодер на рис. 5.4, а аппроксимирует сигнал посредством линейно-ступенчатой функции. Для хорошей аппроксимации скорость стробирования должна быть хотя бы в несколько раз больше скорости изменения сигнала , определяемой скоростью Найквиста. При заданной скорости стробирования качество кодера ограничено двумя типами искажений: перегрузкой по наклону и шумом дробления. Первый связан со слишком малым шагом , недостаточным для слежения за сигналом с крутым наклоном. Второй – со слишком большим шагом для сигнала с малым наклоном. Обычно минимизируют сумму средних квадратов обоих искажений.

Адаптивные ИКМ и ДИКМ. Многие реальные источники квазистационарны, так как на их выходах дисперсия и автокорреляционная функция сигнала медленно меняются со временем. Но кодеры ИКМ и ДИКМ проектируют в предположении, что выход источника стационарен. Эффективность и рабочие характеристики таких кодеров могут быть улучшены, если они будут адаптироваться к медленно меняющейся во времени статистике источника. Одно улучшение, уменьшающее динамический диапазон шума квантования, - это использование адаптивного квантователя. Один из простых способов сводится к применению равномерного квантователя, у которого величина шага квантования меняется в соответствии с дисперсией последних сигнальных отсчетов. Краткосрочная текущая оценка дисперсии может быть рассчитана для входной последовательности . При использовании адаптивной ДМ переменный шаг квантования адаптируется к кратковременным характеристикам сигнала источника, то есть размер шага увеличивается, когда сигнал имеет крутой наклон, и уменьшается, когда сигнал имеет относительно малый наклон.

Пример 5.5.3. Алгоритм Джайанта построения адаптивного квантователя при кодировании сигналов речи использует только один предыдущий отсчет сигнала для установки текущего размера шага квантователя: , где - некоторый множитель, зависящий от уровня квантования отсчета , а - размер шага квантования для обработки .

Если выход источника - квазистационарный, то предсказатель тоже можно сделать адаптивным. Коэффициенты такого предсказателя время от времени изменяются, отражая изменение статистики сигнала источника. Линейные уравнения (5.7) для их расчета остаются справедливыми с заменой функции корреляции по ансамблю отсчетов сигнала на краткосрочную оценку автокорреляционной функции отсчета как случайной величины. Найденные можно передать приемнику вместе с ошибкой квантования . В приемнике есть такой же предсказатель, как и в передатчике. Дополнительная передача величин повышает битовую скорость, что нежелательно. Вместо этого приемник может сам вычислять коэффициенты предсказания, используя и , где . Пренебрегая шумом квантования, заменим на . Тогда можно применить для оценки автокорреляционной функции приемника . Решая (5.7), находят текущие значения коэффициентов предсказания. Такой предсказатель приводит к низкой скорости кодирования данных источника.