
- •5. Кодирование аналоговых источников – оптимальное квантование
- •5.1. Преобразование сигнала из непрерывной в цифровую форму
- •5.2. Функция скорость-искажение
- •5.3. Скалярное квантование
- •И, в частности, для среднеквадратических значений искажений, когда , имеем:
- •5.4. Векторное квантование
- •5.5. Временное сигнальное кодирование
- •5.6. Спектральное кодирование сигнала
- •5.7. Модельное кодирование источника
5.3. Скалярное квантование
Кодируя
источник, квантователь
можно оптимизировать. Пусть заданы: 1)
ФПВ
дискретной по времени и непрерывной по
амплитуде последовательности значений
![]() на входе квантователя; 2)
- число уровней квантования,
на входе квантователя; 2)
- число уровней квантования,
![]() .
Для расчета оптимального скалярного
квантователя
введем некоторую функцию
.
Для расчета оптимального скалярного
квантователя
введем некоторую функцию
![]() ошибки квантования
ошибки квантования
![]() ,
где
,
где
![]() - квантованное значение
.
Выходной уровень
- квантованное значение
.
Выходной уровень
![]() ,
,
![]() ,
для амплитуды входного сигнала
из диапазона
,
для амплитуды входного сигнала
из диапазона
![]() (
(![]() и
и
![]() ).
Оптимальные наборы значений
).
Оптимальные наборы значений
![]() и
и
![]() найдем, минимизируя функционал искажения
найдем, минимизируя функционал искажения
 (5.2)
(5.2)
С
учетом (5.2) конкретизируем необходимые
условия:
![]() и
и
![]() ,
минимума искажений:
,
минимума искажений:

И, в частности, для среднеквадратических значений искажений, когда , имеем:
 (5.3)
(5.3)
то
есть,
![]() - среднеарифметическое
- среднеарифметическое
![]() и
и
![]() ,
а
- центроид
области
между
,
а
- центроид
области
между
![]() и
.
Для реалистичных
можно решить (5.3) численно.
и
.
Для реалистичных
можно решить (5.3) численно.
Неравномерный
квантователь
имеет переменный шаг квантования
![]() ,
зависящий от
,
зависящий от
![]() .
Более прост в реализации равномерный
квантователь. У него - постоянный шаг
квантования
.
Более прост в реализации равномерный
квантователь. У него - постоянный шаг
квантования
![]() .
Этот квантователь получается из (5.3),
если
.
Этот квантователь получается из (5.3),
если
![]() .
Его выходные уровни
.
Его выходные уровни
![]() ,
,
![]() ,
для амплитуды входного сигнала
,
для амплитуды входного сигнала
![]() .
На практике может быть
.
На практике может быть
![]() .
При заданной битовой скорости
бит на отсчет (символ) источника искажения
для неравномерного квантователя меньше,
чем у равномерного. Наименьшее значение
искажений
неравномерного квантователя достигается
для гауссовского источника без памяти.
Тогда
.
При заданной битовой скорости
бит на отсчет (символ) источника искажения
для неравномерного квантователя меньше,
чем у равномерного. Наименьшее значение
искажений
неравномерного квантователя достигается
для гауссовского источника без памяти.
Тогда
![]() (см. пример 5.2.1).
(см. пример 5.2.1).
Пример
5.3.1. Оптимальный
уровневый
(![]() )
неравномерный квантователь для
гауссовской амплитуды сигнала с нулевым
средним и единичной дисперсией, согласно
(5.3), описан в табл. 5.2.
)
неравномерный квантователь для
гауссовской амплитуды сигнала с нулевым
средним и единичной дисперсией, согласно
(5.3), описан в табл. 5.2.
Таблица 5.2. Уровни оптимального уровневого неравномерного квантователя
-
Уровень
1 -0,9816 -1,510
2 0,0 -0,4528
3 0,9816 0,4528
4
 1,510
1,510
Вероятности
символов на выходе квантователя:
![]() - для двух внешних уровней и
- для двух внешних уровней и
![]() - для двух внутренних уровней. Тогда
энтропия дискретного источника
- для двух внутренних уровней. Тогда
энтропия дискретного источника
![]() бит/символ.
бит/символ.
Квантователь
превращает непрерывную амплитуду
источника в дискретную. Дискретные
амплитуды трактуем как символы
![]() с вероятностями
с вероятностями
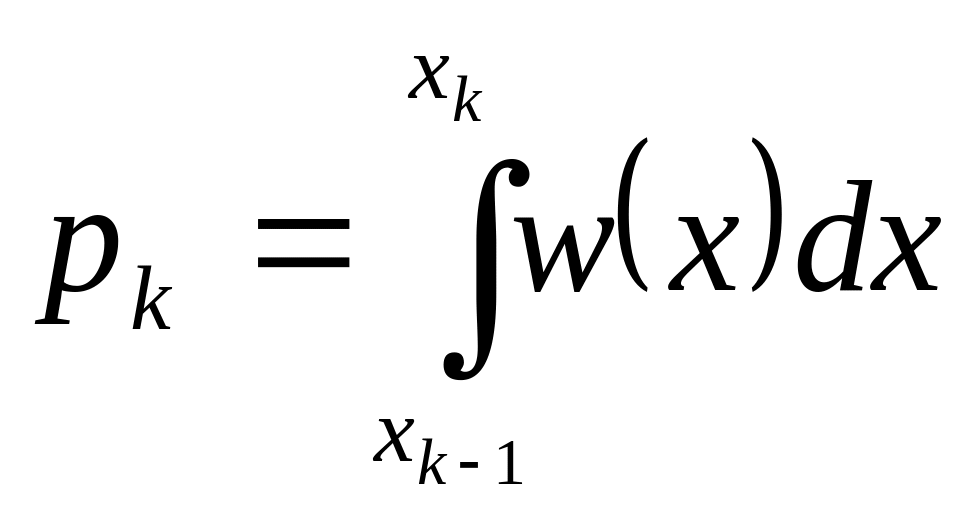 .
Выход квантователя можно подвергнуть
энтропийному кодированию для повышения
эффективности сжатия данных. При
независимых отсчетах амплитуды сигнала
на выходе квантователя получим дискретный
источник без памяти с энтропией
.
Выход квантователя можно подвергнуть
энтропийному кодированию для повышения
эффективности сжатия данных. При
независимых отсчетах амплитуды сигнала
на выходе квантователя получим дискретный
источник без памяти с энтропией
![]() .
.
5.4. Векторное квантование
Изучим
совместное квантование блока символьных
отсчетов или блока сигнальных параметров
- блоковое
(векторное)
квантование.
Его широко применяют для кодирования
речи в цифровых сотовых системах связи
![]() .
Согласно теории искажений
.
Согласно теории искажений
![]() ,
лучшую характеристику можно достичь
векторным, а не скалярным квантованием,
даже если непрерывный источник - без
памяти. Если, кроме того, отсчеты сигнала
или его параметры статистически зависимы,
то эту зависимость можно использовать
посредством совместного квантования
блоков отсчетов или параметров. Так
достигается большая эффективность
(меньшая битовая скорость), чем для
скалярного квантования. Векторное
квантование не ограничивается квантованием
блока сигнальных отсчетов источника.
Его можно использовать для квантования
ряда параметров, извлеченных из данных.
,
лучшую характеристику можно достичь
векторным, а не скалярным квантованием,
даже если непрерывный источник - без
памяти. Если, кроме того, отсчеты сигнала
или его параметры статистически зависимы,
то эту зависимость можно использовать
посредством совместного квантования
блоков отсчетов или параметров. Так
достигается большая эффективность
(меньшая битовая скорость), чем для
скалярного квантования. Векторное
квантование не ограничивается квантованием
блока сигнальных отсчетов источника.
Его можно использовать для квантования
ряда параметров, извлеченных из данных.
Векторное
квантование блоков данных - проблема
распознавания
образов.
Она
включает в себя классификацию этих
блоков через дискретное число категорий
или ячеек, согласно некоторому критерию
точности (например, - среднеквадратичной
погрешности). Пусть на вход квантователя
поступает вектор
![]() блока данных с
вещественными непрерывными амплитудами
компонент (
блока данных с
вещественными непрерывными амплитудами
компонент (![]() )
и известной совместной ФПВ
)
и известной совместной ФПВ
![]() .
Операция квантования описывается
оператором
.
Операция квантования описывается
оператором
![]() :
:
![]() (5.4)
(5.4)
где
![]() - это
-мерный
вектор на выходе квантователя.
Геометрически действие оператора
сводится к следующему. Производится
деление
-мерного
пространства на ячейки. Каждой ячейке
соответствует свое значение вектора
квантования
.
При квантовании каждое значение
- это
-мерный
вектор на выходе квантователя.
Геометрически действие оператора
сводится к следующему. Производится
деление
-мерного
пространства на ячейки. Каждой ячейке
соответствует свое значение вектора
квантования
.
При квантовании каждое значение
![]() заменяется значением
ячейки, куда попал конец вектора
.
Начала всех возможных векторов
и
находятся в начале выбранной системы
координат. Замена
на
ведет к ошибке квантования. За меру
ошибки можно взять искажение (взвешенную
среднеквадратичную ошибку)
заменяется значением
ячейки, куда попал конец вектора
.
Начала всех возможных векторов
и
находятся в начале выбранной системы
координат. Замена
на
ведет к ошибке квантования. За меру
ошибки можно взять искажение (взвешенную
среднеквадратичную ошибку)
![]() ,
где
,
где
![]() - положительно определенная взвешивающая
матрица,
обратная матрице ковариаций входных
данных,
- положительно определенная взвешивающая
матрица,
обратная матрице ковариаций входных
данных,
![]() - символ транспонирования. Среднее по
ряду
входных векторов
искажение
- символ транспонирования. Среднее по
ряду
входных векторов
искажение
![]() ,
где
,
где
![]() ,
,
![]() - вероятность попадания конца вектора
в ячейку
- вероятность попадания конца вектора
в ячейку
![]() ,
и
,
и
![]() .
.
Для квантователя есть условия минимизации среднего искажения . Во-первых, оптимальный квантователь использует выбор по правилу ближайшего соседа:
![]() (5.5)
(5.5)
если,
и только если
![]() .
Во-вторых, каждый выходной вектор
.
Во-вторых, каждый выходной вектор
![]() выбирают
так, чтобы минимизировать среднее
искажение
выбирают
так, чтобы минимизировать среднее
искажение
![]() в ячейке
.
Этот вектор
-
центроид
ячейки
.
в ячейке
.
Этот вектор
-
центроид
ячейки
.
В качестве верхней
границы искажений векторного квантования
можно использовать произведение величин
искажений оптимального скалярного
квантователя, вычисляемых по отдельным
компонентам вектора. Наилучшие
характеристики оптимального векторного
квантователя даются функцией
скорость-искажение
(или обратной к ней функцией
искажение-скорость
![]() ).
Определим функцию
.
Минимально достижимая средняя битовая
скорость, с которой можно передать
векторы
).
Определим функцию
.
Минимально достижимая средняя битовая
скорость, с которой можно передать
векторы
![]() ,
равна
,
равна
![]() бит/отсчет, где
бит/отсчет, где
![]() энтропия квантованного выхода источника,
энтропия квантованного выхода источника,
![]() .
Для заданных значений
.
Для заданных значений
![]() и
(
и
(![]() )
минимально достижимое искажение
)
минимально достижимое искажение
![]() ,
где минимум взят по всем возможным
отображениям
,
где минимум взят по всем возможным
отображениям
![]() и ячейкам квантователя. В пределе получим
искомую функцию искажение-скорость:
и ячейкам квантователя. В пределе получим
искомую функцию искажение-скорость:
![]() (5.6)
(5.6)
Видно, что функцию
искажение-скорость
![]() можно как угодно приблизить к пределу
,
увеличивая размерность
векторов
.
можно как угодно приблизить к пределу
,
увеличивая размерность
векторов
.
На практике ФПВ
![]() данных
может быть неизвестна. Тогда можно
адаптивно выбрать квантованные выходные
векторы, применяя ряд обучающих векторов
данных
может быть неизвестна. Тогда можно
адаптивно выбрать квантованные выходные
векторы, применяя ряд обучающих векторов
![]() числом
числом
![]() .
Итеративный групповой алгоритм (алгоритм
.
Итеративный групповой алгоритм (алгоритм
![]() -средних,
если считать
-средних,
если считать
![]() ),
применяют к обучающим векторам. Алгоритм
итеративно делит
),
применяют к обучающим векторам. Алгоритм
итеративно делит
![]() обучающих векторов на
групп, согласно отмеченным условиям
оптимальности.
обучающих векторов на
групп, согласно отмеченным условиям
оптимальности.
Опишем алгоритм
![]() средних
из
х
шагов
.
На
средних
из
х
шагов
.
На
![]() ом
шаге инициализируют номер итерации:
ом
шаге инициализируют номер итерации:
![]() .
Выбирают ряд выходных векторов
.
Выбирают ряд выходных векторов
![]() ,
,
![]() .
На
.
На
![]() ом
шаге обучающие векторы
ом
шаге обучающие векторы
![]() делят на группы
делят на группы
![]() ,
согласно правилу ближайшего соседа:
,
согласно правилу ближайшего соседа:
![]() ,
если
,
если
![]() для всех
для всех
![]() .
На
.
На
![]() ем
шаге пересчитывают выходные векторы
каждой группы для следующей
ем
шаге пересчитывают выходные векторы
каждой группы для следующей
![]() -ой
итерации. То есть, вычисляют центроиды
-ой
итерации. То есть, вычисляют центроиды
![]() ,
,
для обучающих векторов каждой группы.
Находят результирующее искажение
,
,
для обучающих векторов каждой группы.
Находят результирующее искажение
![]() на
на
![]() -ой
итерации. На
ом
шаге тестирование заканчивают, если
-ой
итерации. На
ом
шаге тестирование заканчивают, если
![]() окажется меньше заданной величины.
Иначе следует идти на
шаг.
окажется меньше заданной величины.
Иначе следует идти на
шаг.
Алгоритм -средних приводит к локальному минимуму искажения для каждой выборки начальных выходных векторов , . Затем можно найти глобальный минимум искажения по всем выборкам.
Пример 5.4.1. Пусть
![]() и
и
![]() - случайные величины с равномерной
совместной ФПВ
- случайные величины с равномерной
совместной ФПВ
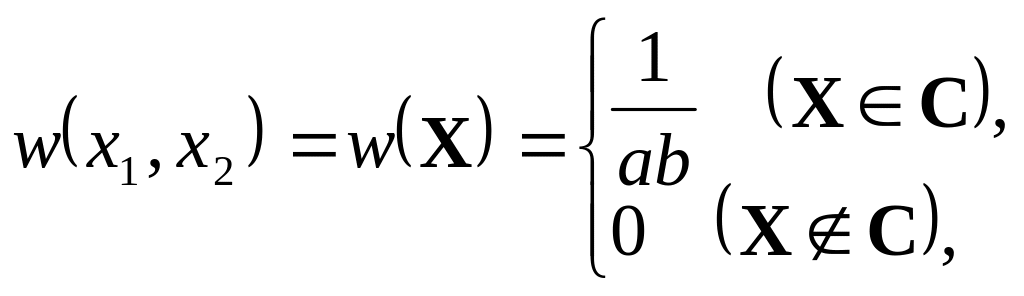
где
![]() - прямоугольная область со сторонами
и
- прямоугольная область со сторонами
и
![]() ,
показанная на рис. 5.1.
Прямоугольник повернут на
,
показанная на рис. 5.1.
Прямоугольник повернут на
![]() относительно горизонтальной оси. На
рис. 5.1 показаны также собственные
плотности вероятности
относительно горизонтальной оси. На
рис. 5.1 показаны также собственные
плотности вероятности
![]() и
и
![]() .
.
Величины
![]() и
и
![]() квантуем раздельно и равномерно с шагом
.
Тогда необходимо иметь
квантуем раздельно и равномерно с шагом
.
Тогда необходимо иметь
![]() уровней квантования и
уровней квантования и
![]() бит для кодирования вектора
бит для кодирования вектора
![]() .
Скалярное квантование обеих компонент
и
эквивалентно векторному квантованию
с числом уровней
.
Скалярное квантование обеих компонент
и
эквивалентно векторному квантованию
с числом уровней
![]() .
Квантование всей области на рис. 5.1, куда
входит область
,
произведем посредством квадратных
ячеек со стороной
.
Так как
.
Квантование всей области на рис. 5.1, куда
входит область
,
произведем посредством квадратных
ячеек со стороной
.
Так как
![]() при
при
![]() ,
то такое квантование нецелесообразно:
приводит к неоправданному увеличению
битовой скорости. Теперь покроем такими
же квадратными ячейками только область
.
Число уровней векторного квантования
(ячеек)
,
то такое квантование нецелесообразно:
приводит к неоправданному увеличению
битовой скорости. Теперь покроем такими
же квадратными ячейками только область
.
Число уровней векторного квантования
(ячеек)
![]() ,
а его скорость
,
а его скорость
![]() .
Разность в битовой скорости скалярного
и векторного квантования
.
Разность в битовой скорости скалярного
и векторного квантования
![]() .
В частности, если
.
В частности, если
![]() ,
то
,
то
![]() бит/вектор, и векторное квантование на
бит/вектор, и векторное квантование на
![]() бит/отсчет лучше, чем скалярное при тех
же искажениях.
бит/отсчет лучше, чем скалярное при тех
же искажениях.



Рис. 5.1. Равномерная ФПВ в двух измерениях
Линейное преобразование (поворот на ) декоррелирует случайные величины и , делая их независимыми. Тогда скалярное и векторное квантование одинаково эффективны. В общем случае линейное преобразование может декоррелировать вектор случайных величин, но не приводит к статистически независимым случайным величинам. Поэтому по своим характеристикам скалярный квантователь не может превзойти векторный.
