5. Кодирование аналоговых источников – оптимальное квантование

5.1. Преобразование сигнала из непрерывной в цифровую форму

В цифровых системах передачи непрерывные сообщения передают дискретными сигналами . Преобразование сигнала из непрерывной в цифровую форму означает его дискретизацию по времени и квантование по уровню. Пусть непрерывный сигнал аналогового источника - реализация случайного стационарного процесса с ограниченной полосой. Выход источника превратим в дискретную последовательность отсчетов, взятых со скоростью Найквиста (см. (2.15)). Квантуем их по уровням. Каждый дискретный уровень амплитуды кодируем последовательностью двоичных символов. Для уровней квантования надо иметь бит/отсчет, если - целая степень , иначе - . Квантование позволяет сжать данные. Энтропийное кодирование повышает эффективность кода, но ведет к искажению формы сигнала и потере точности его отображения. Искажения минимизируют оптимальным квантованием.

Пример 5.1.1. Приведем примеры простых кодов . Слова натурального двоичного кода (НДК) – двоичные номера уровней квантования непрерывного сигнала. НДК просто реализовать, и он удобен для обработки на ЭВМ. Симметричный двоично-числовой код отображает биполярные квантованные отсчеты сигнала. Высший разряд каждого кодового слова информирует о знаке отсчета, а остальные разряды – об абсолютном значении отсчета в НДК. Код Грея связан с НДК: , , , , , где и - кодовое слово НДК и кода Грея, соответственно. По сравнению с НДК код Грея имеет особенности, позволяющие повысить быстродействие кодирующих устройств:

1) любые два кодовых слова соседних уровней квантования различны лишь в одном разряде;

2) вдвое реже смена значений элементов в каждом разряде при переходе от одного кодового слова к другому, чем в НДК.

5.2. Функция скорость-искажение

Возьмем источник без памяти. Он имеет непрерывный амплитудный выход с функцией плотности вероятности (ФПВ) отсчета, квантованный амплитудный алфавит и меру искажения на отсчет , где , , , - полное число отсчетов, - целый параметр, . Для среднеквадратического искажения . Среднее искажение по отсчетам . Его математическое ожидание - . Наименьшая скорость в бит/отсчет для источника без памяти с искажением - функция скорость-искажение (ФСИ),

(5.1)

где - средняя взаимная информация и . Скорость обычно уменьшается с ростом максимума величины допустимых искажений .

Пример 5.2.1. Возьмем гауссовский источник без памяти с ФПВ , математическим ожиданием и дисперсией . Из (5.1) для среднеквадратичной ошибки на символ ( ) в качестве меры искажения

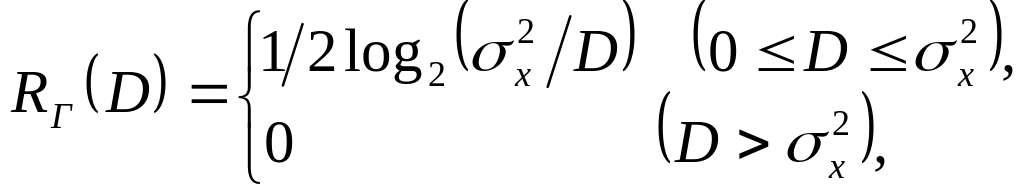
где при никакой информации передавать не надо.

Теорема Шеннона о кодировании источника с заданной мерой искажения. Есть схема кодирования, отображающая выход источника в кодовые слова так, что для любого данного искажения минимальная скорость бит на символ (отсчет) источника достаточна, чтобы восстановить исходный сигнал со средним искажением, как угодно близким к .

Доказательство теоремы ясно: для любого источника дает нижнюю границу скорости источника, возможной для данного уровня искажения. Дадим оценки границ изменения для любого дискретного по времени и непрерывного по амплитуде источника : ( - нижняя граница Шеннона). Для среднеквадратичной ошибки , где - дифференциальная энтропия источника без памяти с непрерывной амплитудой.

Пример 5.2.2. В табл. 5.1 представлены дифференциальная энтропия и сравнение скорости и искажений для х моделей сигнала .

Таблица 5.1. Дифференциальная энтропия и сравнение скорости и искажений для х распространенных моделей сигналов

ФПВ Бит/отсчет дБ

Гауссовское Равномерное Лапласа Гамма