3. Математический аппарат представления информационных объектов и процессов.

Этот аппарат рассматривается в раннем подходе, условно называемом кибернетическим: где всякое целенаправленное поведение рассматривается как управление, на языке и методами управления.

Язык управления – это использование понятия объект, среда, объективная связь, алгоритм, и т.д.

Методы управления – идентификация, планирование, эксперимента исследование операций, адаптация, распознавание и др.

Управление – процесс организации такого целенаправленного воздействия на некоторую часть среды, называемую Объектом Управления, взаимодействующего с этим объектом.

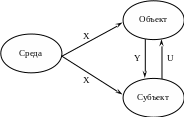
X – воздействие среды.

Y – воздействие объекта.

U – специальное организованное воздействие, которое мы называем управление.

X Y – субъективное воздействие.

Состояние Y объекта влияет на состояние потребностей субъекта.

Потребности:

(1) А = ( , … , ) | - состояние i-ой потребности субъекта, которое выражается неотрицательным числом, характеризующим насущность и актуальность этой потребности.

(2) , где R - множество ресурсов. Это зависимость выражает неизвестную, но существующую связь потребностей с состоянием X среды и поведением U субъекта.

Пусть - решение задачи (2) (то есть оптимальное поведение субъекта при его минимальных потребностях).

Способ решения задачи называют алгоритмом управления:

(3) , где

- потребность,

t – отражает изменение их потребностей из-за жизнедеятельности субъекта, а не только из-за влияния среды,

X – состояние среды

- может быть любой, но скорее всего, эта зависимость будет иметь рекуррентный характер:

(4) , то есть на каждом шаге улучшаем управление

(5) , например, в смысле:

(6) , то есть в смысле снижения уровня всех потребностей.

Сам процесс может реализовываться на осознанном уровне – то есть, осознаётся процесс удовлетворения потребностей – это заставляет декомпозировать алгоритм управления и вводить промежуточную стадию – формулировку цели управления, то есть действовать по 2^ух стадийной схеме:

(

1

7)

2

(8) - это определение цели управления, где – алгоритм синтеза цели по потребностям и состоянию среды.

- цель удобно называть «модель потребного будущего», то есть в процессе выполнения субъект «отчуждает» свои потребности и переводит их на язык состояний объекта:

(9)

Именно это (моделирование, формализация, предписание) позволяет передать процедуру синтеза и реализации управления другому лицу или автомату.

На 2ой стадии определяется и используется возможность формального аппарата синтеза управления:

, где – алгоритм управления.

Структурная схема системы управления (СУ).

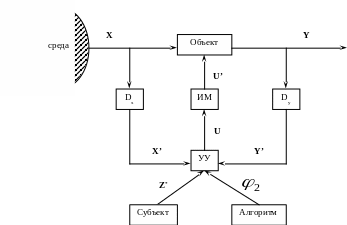
Исходную Y (информацию)

(11) I = <X’, Y’> , образуют результат измерения:

(12) X’ = D_x (X)

Y’ = D_y (Y)

УУ

U – это лишь информация о том, в какое положение должны быть приведены управляемые входы объекта.

U – это результат работы алгоритма:

(13) , т.е. управление в широком смысле определяется четвёркой:

(14)

Для принятия решения о создании ИС – т.е. основы системы управления – надо рассмотреть этапы алгоритмического синтеза.

Предметную область характеризует:

1. Отсутствие математического описания и необходимость его для управления.

2. Стохастичность поведения, вызванная неизбежным обилием всякого рода второстепенных с точки зрения целей управления, процессов.

3. Негативность к управлению, связанная с «независимостью» системы и создаваемого управления.

4. Нестационарность, вызванная её сложностью и проявляющаяся в дрейфе характеристик системы, в изменении её параметров, в эволюции системы во времени.

5. Невоспроизводимость экспериментов, которая проявляется в различной реакции системы на одну и ту же ситуацию или управление в разные t[c]. То есть сложная развивающаяся система всё время как бы перестаёт быть самой собой.

Управление проектированием сложных систем производится посредством использования информационных систем.

Проектирование ИС состоит из следующих этапов:

1. Формулирование целей – их множество и все его

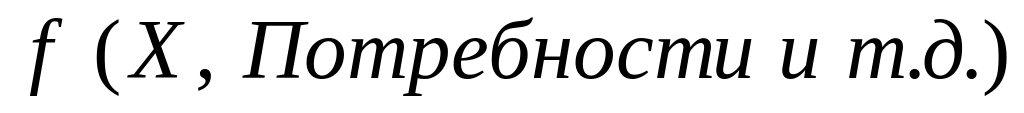
Пусть измеряемые выходы ОУ характеризуют его (ОУ) состояние:

(15) , где – характеристики объекта.

(16) , где – характеристики среды.

Целевые переменные, определяемые субъектом:

Пусть также существует строго определённая и известная связь

(17)

Выделяют 3 вида целей:

• Цель стабилизация (приравнять к эталону) – целевых переменных k₁

(18) , где – требуемый субъекту уровень целевой переменной при состоянии среды и потребностями .

• Цель ограничения («ограничить») требует выполнения неравенства:

(19) , где – верхняя граница изменения целевой переменной , определяемая субъектом в ситуации .

• Цель экстремальности («экстремизировать») – стремится поддержать в экстремальном состоянии 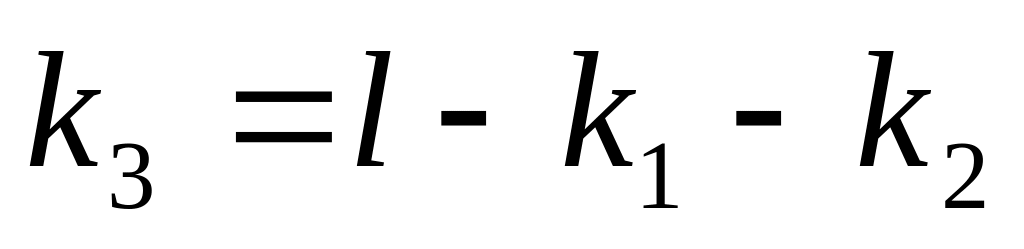целевых переменных:

(20)

Таким образом, цель:

(21) – это набор требований указанного вида и однозначно определяющееся числом (потребность) и (граничные значения потребности). А множество целей определяется путём задания диапазонов изменения параметров:

(22)

2. Определение объекта управления (выделение той части среды субъекта, состояние корой он может изменить и тем самым воздействовать на свои потребности)

Но, выбирая ОУ, надо сделать его min! Но существование ограничение – достижимость в рамках выделенного для этого ресурса!

То есть для любого Х должно найтись управление (где R – ресурс), с помощью которого можно добиться любой допустимой цели

Введём предикат – состояние или условие выполнимости задачи:

(23) , где

- объект управления, количество переменных состояний среды и связей между ними (модель), которые следует отнести к объекту управления.

(24) – это выражение связывает состояние X среды цель и объект .

Введём объём объекта в виде . Тогда задача определения сводится к следующей оптимизационной задаче:

(25) , где

(26)

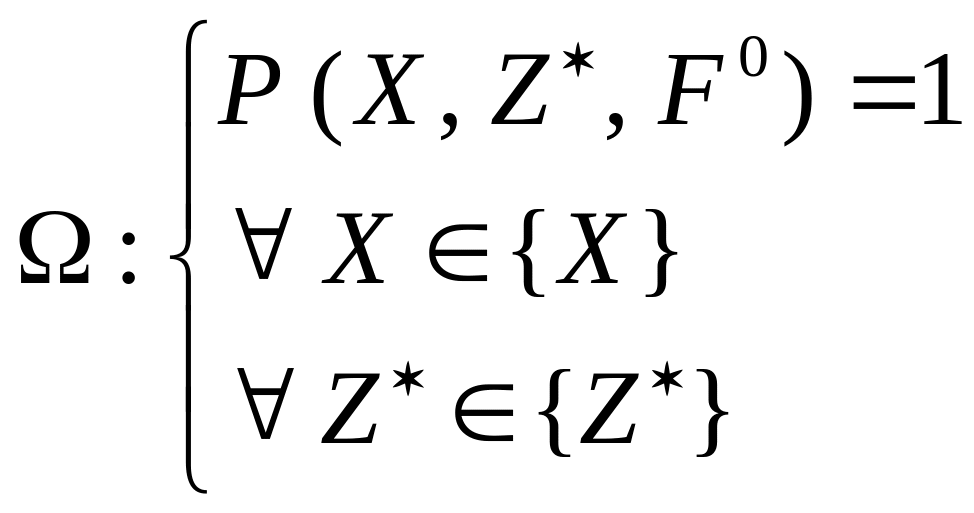
– это множество переменных состояния, целей субъекта и состояния, когда баланс целей и возможностей можно реализовать.

Если (25) не выполняется, то объект

(27)

следует расширить за счёт управления состоянием среды, то есть присоединяя часть среды к объекту:

(

U₁

U₂

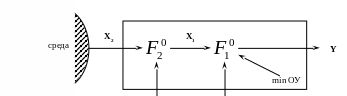28) , где – новое состояние среды.

Теперь

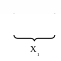( 29)

и новый объект

(30) , где – условное сложение,

управляется в большей мере, чем исходный . Однако ограничения ресурса .

(31)

могут сузить возможность управления.

Можно ввести понятие управляемости объекта:

(32) , где – плотность распределения состояния среды и целей , можно задачу синтеза объекта сформулировать по-другому:

(33)

где

– максимальный допустимый объём объекта, определяемый ресурсом, выделяемым на изучение такого объекта (25) и (33) можно различить только экспертным путём.

измеряется в количестве .

Методы экспертных оценок (ЭО).

Обоснование их объективности предполагает, что индивидуальная ЭО отражает опыт и знания специалиста от объективной действительности.

Неизвестная (описываемая) характеристика исследуемого явления понимается как случайная величина, и что отражением закона распределения этой характеристики является индивидуальная оценка специалиста о достоверности и значимости того или иного события.

Когда такие оценки получены от группы экспертов, предполагается, что истинные значения исследуемой характеристики находится внутри диапазона оценок и что обобщённое коллективное мнение является достоверным.

Последующее этапы управления предметной областью сведены с решением задачи создания её (ПО) модели, которая нужна для синтеза управления . Только с помощью модели объекта можно построить управление , переводящее объект в требуемое (целевое) состояние .

Модель , связывающая входы и с выходами , определяется структурой и параметрами , представима в виде двойки:

3. Структурный синтез модели.

Надо определить структуру , то есть модель объекта с точностью до значений её параметров .

Этап структурного синтеза включает: определение внешней структуры модели, декомпозицию модели, определение внутренней структуры и элементов модели

Синтез внешней ST модели – это содержательное описание её входов X и U, а также выхода Y без цифр внутренней ST объекта. То есть, объект рассматривается как “чёрный ящик” с n + q входами и m выходами, как (n + q) * m – ?.

Для этого производится отбор прецедентов.

Декомпозиция модели заключается в том, чтобы используя априорные сведения о ST объекта, упростить задачу синтеза структуры модели.

Синтез внутренней ST модели сводится к определению ST оператора F модели объекта или её элемента с точностью до её параметра C. Это значит, что параметры становятся переменными модели:

Y = F(X, U, C),

где F – оператор преобразования со структурой ST, параметры которого для удобства внесены в переменные C. Представление в таком виде оператора преобразования модели называют “параметризацией” модели, что эквивалентно заданию его структуры.

Этап 4. Идентификация ? модели. Этот этап связан с определением численных значений параметров C( , …, ) в решении N-ного функционирования объекта, то есть без организации специальных экспериментов с ним. Делается это стандартными приёмами идентификации.

Однако, для выяснения ? выхода объекта Y = f(U) от управляемых входов и, необходимо их (U) предварительно изменять, то есть экспериментировать с объектом.

Но ? объект “не любит” эксперименты, нарушающие его N-ное функционирование. Поэтому эксперимент, который нельзя избежать, следует проводить, минимально возмущая объект, но так при этом, чтобы получить максимальный Y о влиянии варьируемых параметров на выход объекта. Этому служит эр-и.

Планирование эксперимента. Здесь главным является синтез плана эксперимента, позволяющий с минимальной эффективностью определить искомые параметры модели объекта управления.

Для статического объекта этот план U представляет собой набор состояний управляемого входа объекта

,

а для динамического – план-функцию

,

то есть программу изменения во времени входа объекта.

Эксперимент на объекте даёт возможную определённую реакцию объекта на это воздействие.

В статическом случае эта реакция имеет вид

,

а в динамическом

Полученный при этом Y и является исходной для определённых параметров C модели F:

,

Что осуществляется методами идентификации.

План эксперимента ? :

а) структурой S модели F;

б) ресурсом планирования R, ? образуется выделяемыми на эксперимент средствами (временными, материальными, ? и т. п.), а также областью планирования, общей предали изменению входа U объекта в процессе планирования;

в) критерием планирования K, который определяет эффективность плана U. Задаётся он обычно на дисперсионной матрице искомых параметров модели. Синтез оптимального плана осуществляется решением следующей оптимизационной задачи:

- к-й оптимальный план.

6. Синтез управления. На этом этапе принимается решение о том, каково должно быть управление U, чтобы достигнуть заданной цели управления 2-х в. объекта. Это решение опирается на имеющуюся модель F, заданную 2-х, на полученную Y о состоянии среди X и выделенный ресурс управления R, ? представляет собой ограничения, накладываемые на управление U в связи со спецификой объекта и возможностями системы управления.

Ситуация, которая складывается в процессе управления, характеризуется тройкой

.

Достижение целей управления 2-х эквивалентно выполнению условий

,

? с учётом имеющейся модели F можно записать в канонической векторной форме:

,

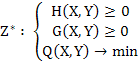где компоненты H, G и Q являются:

.

Реализовать условия (W) можно только соответствующим изменением состояния объекта Y управление. Это означает, что их выполнение возможно только соответствующим выбором управления U, так как состояние среды X изменяется независимо от ?. Эти соображения приводят к следующей экстремальной задаче:

,

решение которой является оптимальным управлением.

Способы решения задач (WW) зависят от структуры F модели объекта. Если объект статический, то есть F дискретна, то получаем задачу математического программирования. Если объект динамический, то решают вариационную задачу.

7. Реализация управления или обработка в объекте оптимального решения , полученного на предыдущем этапе. Реализовав управление, и убедившись, что цель управления не достигнута, приходится возвращаться к одному из предыдущих этапов.

Математический аппарат и модели информационных объектов и процессов.

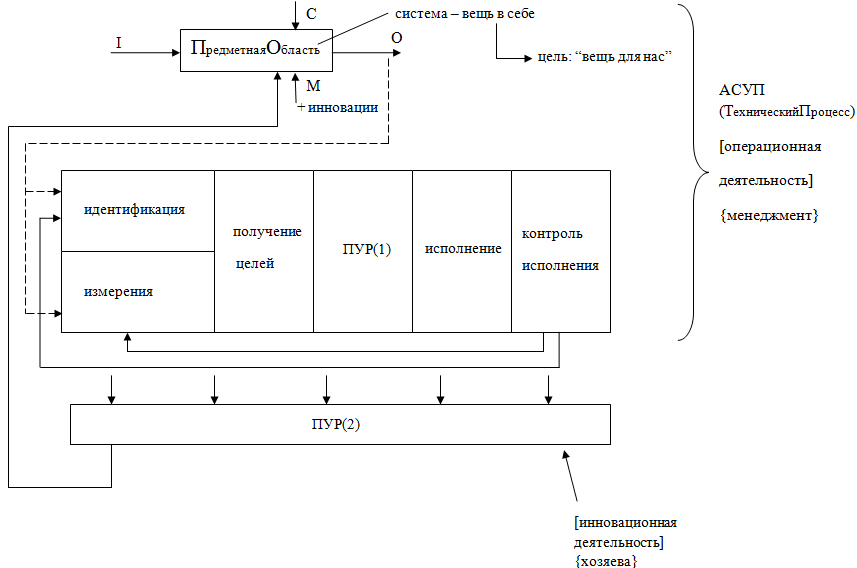
Управление включает в себя:

1. познания (измерения) реальных условий существования системы, а также ограничений (предельные значения параметров, переменных состояния и окружающей среды);

2. выработка целей (то есть отражение объектного оптимизма) функционала управляемой системы;

3. принятие управляемого решения (выработка распоряжения), то есть констатация обязательности устранения расхождения между желаемым оптимумом и реальным значением функционала существования системы;

4. исполнение (практика), то есть реализация исполнительными органами близких к оптимальным условий существования системы;

5. контроль исполнения (обратная связь), то есть познание новых условий существования системы, возникших вследствие управления ими.

Для построения ИС важно определение структуры системы – совокупность связей между элементами системы, ограничивающих их взаимодействие.

Классический подход к изучению взаимосвязей предусматривает рассмотрение их как отражение связей между отдельными подсистемами. Этот подход рассматривается при создании простых объектов предметной области. Реальный объект разбивается на отдельные подсистемы, то есть выбираются исходные данные Д системы, моделируются и ставятся цели Ц, отражающие отдельные стороны процесса моделирования. По сути совокупности исходных данных ставится ель моделирования отдельной стороны функционирования системы. На базе этой цели формируется некая компонента К, а совокупность компонент объединяется в модель М.

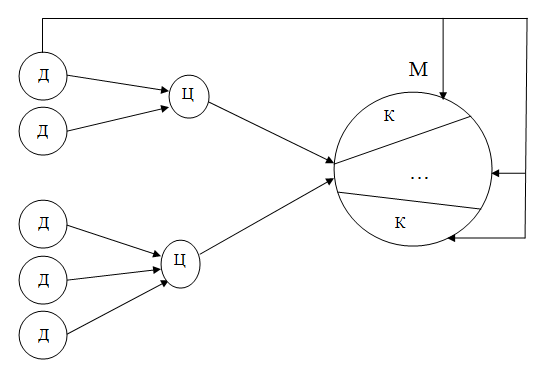
Таким образом, разработка М означает суммирование компонент в единую модель, причём любая из решает свои собственные задачи и изолирована от других частей модели.

Это приемлемо, если возможно разделение и взаимно независимое рассмотрение отдельных сторон функционирования реального объекта.

Этот подход характеризуют 2 отличительные черты:

1. наблюдается движение от частного к общему;

2. не учитывается возникновение нового системного эффекта.

Представим процесс синтеза М на базе системного подхода:

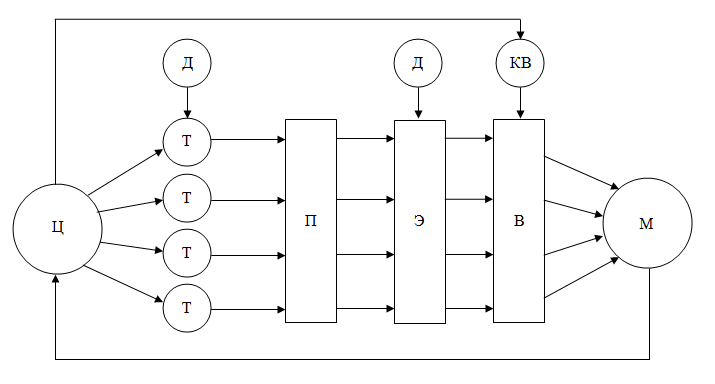
На основе данных Д, которые известны из анализа внешней системы:

1. формируются ограничения, которые накладываются на систему сверху или исходя из возможностей её реализации,

2. определяются цели функционирования,

3. формируются исходные требования Т к системе.

На базе требований формируются некоторые подсистемы П, элементы реализации Э и осуществляется наиболее сложный этап синтеза (выбор В составляющих системы) с применением специальных критериев выбора КВ.

Моделирование в неизменных ситуациях – это означает постоянство во времени свойств модели, окружающей среды и самой системы. В таком режиме остаются неизменными во времени такие данные:

1. первичная чувственная информация;

2. вектор восприятия;

3. сущность объекта.

Так что задача исследования сводится к установлению отношений этих величин.

Поскольку нас здесь интересуют прежде всего формальные, то есть в сущности математические соотношения, которые всегда связывают измеримые величины, то мы должны прежде всего решить вопрос об изменении всех участвующих в отражении величин.

4. Основные элементы теории нечетких объектов; нечеткие множества, системы и семейства нечетких множеств; меры близости нечетких объектов; меры релевантности; отношения релевантности нечетких объектов

Нечеткие множества.

Для начала дадим определение нечеткого множества, чтобы определить тот объект, с которым мы будем работать на протяжении всех лекций.

В математике давно используется понятие множества – совокупности объектов, выделенных по некоторому признаку. Это понятие является базовым в современной математике и потому не определяется строго, формально. Так, если задано некоторое базовое множество X (конечное или бесконечное), то его подмножеством (четким подмнжеством) A называется любое множество, содержащее в себе только элементы множества X (хотя, может быть, и не все его элементы).

Любое подмножество A множества X можно описать его функцией принадлежности A : X {0; 1} m , значение которой для элемента xX равно единице в том случае, если этот элемент принадлежит множеству A, и нулю – в противном случае.

Соответствие между подмножествами множества X и всевозможными функциями принадлежности m : X {0; 1} является взаимно однозначным, то есть, определив некоторое подмножество, мы можем определить его функцию принадлежности, и обратно, задание функции m : X {0; 1} задает и подмножество множества X.

В четком множестве любой элемент может или принадлежать ему, или не принадлежать, поэтому функция принадлежности принимает лишь два возможных значения – ноль или единица.

В нечетком же множестве (точнее, в нечетком подмножестве базового множества X) любой элемент x X может принадлежать множеству с некоторой степенью достовер ности, принимающей значения от нуля (элемент достоверно не принадлежит множеству) до единицы (элемент достоверно принадлежит множеству). Соответственно и функция принадлежности нечеткого множества может принимать любое значение из отрезка [0; 1].

Мы определим понятие нечеткого множества через его функцию принадлежности. Пусть X – некоторое обыкновенное (четкое) множество. В дальнейшем мы будем рассматривать его нечеткие подмножества.

Определение 1. Нечетким множеством A~ в X называется функция m_А~: X [0; 1] , которая каждому из элементов множества X ставит в соответствие степень его принадлежности нечеткому множеству A~ .

Зачем же было введено понятие нечеткого множества? Для того же, для чего вводятся и другие математические объекты – чтобы описывать окружающий нас мир. В действительности большинство понятий, которые используют люди в повседневной жизни, являются нечеткими! Когда сапожник ждет около трех минут после нанесения клея перед склеиванием, когда хозяйка в соответствии с рецептом кладет в суп две щепотки соли, когда менеджер в коммерческой фирме выполняет указание руководства существенно повысить объемы продаж – все они выполняют нечеткие инструкции, сформулированные неформально с помощью разговорного языка. Даже формально четкие понятия, используемые в обыденной жизни, воспринимаются людьми как нечеткие. Например, в рецепте может быть четко указано «две чайные ложки соли», но хозяйка понимает, что блюдо не будет испорчено и если будет положено две с половиной ложки, не говоря уже о том, что чайные ложки, вообще говоря, бывают разной емкости.

Удобным способом математического описания неформальных понятий, подобных упомянутым выше, являются нечеткие множества6.

Язык нечетких множеств имеет существенные преимущества перед языком теории вероятностей в том случае, когда оценки получаются из опроса экспертов. Известно, что люди в большинстве своем неправильно оценивают вероятности (особенно большие и малые). Потому требовать от экспертов – специалистов в конкретных предметных областях, а не математиков, оценок в форме распределения вероятности зачастую невозможно8. Использование же полученных результатов для принятия решений можно квалифицировать как самонадеянное. Описание в форме нечетких множеств гораздо менее требовательно к квалификации экспертов и зачастую гораздо точнее отражает суть дела и имеющуюся у ЛПР информацию.

Конечно, за это удобство приходится платить. Предлагаемые теорией решения, основанные на нечеткой информации, и сами несут на себе печать нечеткости. Они могут рассматриваться лишь как рекомендации для ЛПР, требуя от него выбора одного из предлагаемых вариантов. Тем не менее, даже этот факт можно рассматривать как достоинство теории – он показывает, как увеличение информированности ЛПР сказывается на достоверности и правильности принимаемых решений.

Математическая часть.

Нечёткое (или размытое, расплывчатое, туманное, пушистое) множество — понятие, введённое Лотфи Заде в 1965 г. Л. Заде расширил классическое канторовское понятие множества, допустив, что характеристическая функция (функция принадлежности элемента множеству) может принимать любые значения в интервале [0,1], а не только значения 0 или 1.

Связь с теорией вероятностей.

Теория нечётких множеств в определенном смысле сводится к теории случайных множеств и тем самым к теории вероятностей. Основная идея состоит в том, что значение функции принадлежности можно рассматривать как вероятность накрытия элемента некоторым случайным множеством.

Однако при практическом применении аппарат теории нечётких множеств обычно используется самостоятельно, выступая конкурентом к аппарату теории вероятностей и прикладной статистики.

Нечёткие системы управления.

В настоящее время начинают находить широкое применение так называемые нечеткие системы управления (fuzzy-системы), основанные на нечеткой логике и использующие теорию нечётких множеств. Особенно эффективно применение нечетких систем управления там, где объект управления достаточно сложен для его точного описания и существует дефицит априорной информации о поведении системы. Область применения нечетких систем управления показана на рис.1.

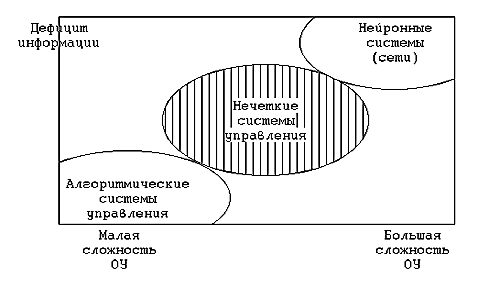
Рис. 1. Сфера применения нечетких систем управления.

Принцип действия нечетких систем управления основан на выполнении нечеткого логического вывода типа < Если А, то Б >. Нечеткие системы имеют базу знаний и зачатки искусственного интеллекта.

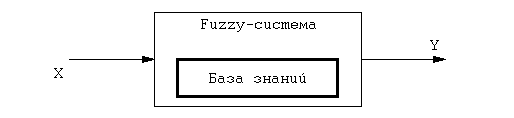
Рис.2. Простейшая одновходовая нечеткая система.

Простейшая система управления, функциональная схема которой показана на рис. 2, реализует один восходящий нечеткий вывод, схему которого можно представить в следующем виде

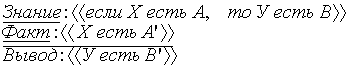
Здесь  - описательная информация - лингвистические переменные, представляемые в виде нечетких множеств 

Недостатками нечетких систем являются:

• отсутствие стандартной методики конструирования нечетких систем;

• невозможность математического анализа нечетких систем существующими методами;

• применение нечеткого подхода по сравнению с вероятностным не приводит к повышению точности вычислений.

Семейства нечётких множеств.

Семейства нечётких множеств – это есть множества, элементами которого являются нечёткие множества.

Если {Ay} - конечное или бесконечное семейство нечетких множеств с функциями принадлежности m(x,y), где _y – параметр семейства.