- •Взаимодействие зарядов. Закон Кулона.
- •Электрическое поле. Напряженность поля.
- •Суперпозиция полей. Поле диполя. Напряженность поля электрического диполя.
- •4. Линии напряженности. Поток вектора напряженности.
- •5.Теорема Гаусса. Независимость потока от поверхности. Доказательство теоремы.
- •6.Напряженность поля для различных конфигураций его источника.
- •2. Поле двух разноименно заряженных плоскостей.
- •7.Работа сил электростатического поля.
- •8.Потенциал
- •9.Связь между напряженностью электрического поля и потенциалом.
- •10.Полярные и неполярные молекулы.
- •11.Диполь в однородном и неоднородном электрических полях.
- •12.Поляризация диэлектриков. Связь поляризации и связанных зарядов.
- •Связь поляризации и связанных зарядов.
- •13. Поляризация и плотность связанных зарядов.
- •14.Описание поля в диэлектриках. Вектор электрического смещения. Диэлектрическая проницаемость.
- •15.Поле внутри плоской пластины.
- •16.Преломление линий электрического смещения.
- •16.Взаимодействие токов.
- •Магнитное поле .Магнитный момент.
- •Поле прямого и кругового токов.
- •Циркуляция вектроа в. Поле соленоида.
- •Сила, действующая на ток в магнитном поле. Сила Ампера для дифференциации силы и элемента длины.
- •Сила Лоренца. Ее действие на движущиеся заряды.
- •Контур с током в магнитном поле. Действие момента сил на контур с током, сила, действующая на контур в неоднородном поле.
- •Работа, совершаемая при перемещении тока в магнитном поле.
- •Магнитное поле в веществе. Намагниченность.
- •Описание поля в магнетиках. Напряженность поля. Магнитная восприимчивость и магнитная проницаемость.
- •Преломление линий магнитной индукции.
- •Классификация магнетиков.
- •Диамагнетизм. Ларморова прецессия.
- •Парамагнетизм.
- •Ферро и антиферромагнетизм. Доменная структура.
- •Явление электромагнитной индукции.
- •Электродвижущая сила индукции.
- •Токи Фуко.
- •Явление самоиндукции.
- •Энергия магнитного поля.
- •Электромагнитное поле. Вихоевое электрическое поле.
- •Ток смещения.
- •Электромагнитное поле. Уравнения Максвелла в интегральной форме.
- •Теория Дурде. Закон Ома. Закон Джоуля-Ленца.
- •Основы квантовой теории твердых тел.
- •Контактная разность потенциалов
Контур с током в магнитном поле. Действие момента сил на контур с током, сила, действующая на контур в неоднородном поле.
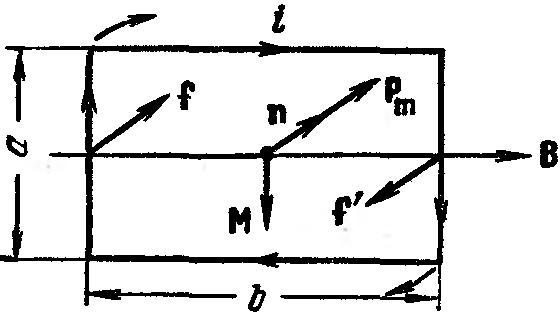
Пусть прямоугольный плоский контур с током помещается в однородном магнитном поле. Если контур ориентирован так, что вектор В параллелен его плоскости (рис. 87), то стороны, имеющие длину b, не будут испытывать действия сил, так как для них в формуле (46.5 df =
Рис. 87. |
Рис. 88. |
М = f b = iBab.
Учитывая, что ab равно площади контура S, а iS есть величина магнитного момента pm, можно написать
M = pm В. (48.1)
Эта формула совпадает по существу с формулой (39.3 ).
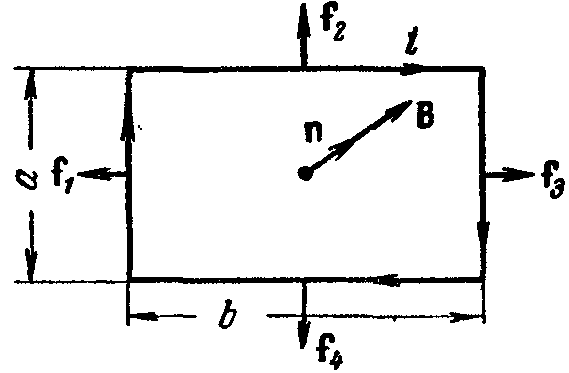
Момент М стремится повернуть контур так, чтобы его магнитный момент рm выстроился по направлению поля В. Такая ориентация контура показана на рис. 88.
В этом случае f1 = f3 = iBa, f2 = f4 = iBb. Направления всех сил лежат в плоскости контура. Видно, что вращательный момент в этом случае не возникает. Поскольку поле однородно, равнодействующая сил равна нулю; силы лишь растягивают контур, но сместить его не могут. Если повернуть контур на 180° (или изменить направление поля на обратное), то направления всех сил изменятся на противоположные, и они будут не растягивать, а сжимать контур.
Рис. 89 |
dM = iB dh b,
где b – длина полоски. Произведение bdh дает площадь полоски dS. Таким образом,
dM = iBdS.
Беря попарно силы, приложенные к противолежащим элементам контура, и суммируя их моменты, получим результирующий момент, действующий на контур:
![]() ,
,
аналогичный формуле (48.1).
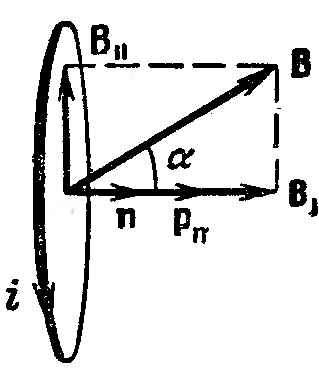
При произвольной ориентации контура (рис. 90) магнитную индукцию В можно разложить на составляющие: B – перпендикулярную и В – параллельную плоскости контура, и рассматривать действие каждой составляющей отдельно. Составляющая B будет обусловливать силы, растягивающие или сжимающие контур.
Составляющая В, величина которой равна В sin ( – угол между pm и В), приведет к возникновению вращательного момента, который можно вычислить по формуле (48.1 M = pm В):
Рис. 90. |
Принимая во внимание взаимную ориентацию векторов М, pm и В, формулу (48.2) можно записать в виде
М = pm В. (48.3)
Для того чтобы угол между векторами pm и В увеличить на d, нужно совершить против сил, действующих на контур в поле, работу
dА = M d = pm B sin d. (48.5)
Поворачиваясь в нервоначальное положение, контур может возвратить затраченную на его поворот работу, совершив ее над какимй-либо телами. Следовательно, работа (48.5) идет на увеличение энергии W, которой обладает контур с током в магнитном поле,
dW = pm B sin d.
Интегрируя, находим, что
W = – pm B cos + const.
Если положить const = 0, формула приобретает вид
W = – pm B cos = – pmВ (48.6)
Отметим, что формула (48.6) аналогична выражению для энергии, которой обладает диполь в электрическом поле.
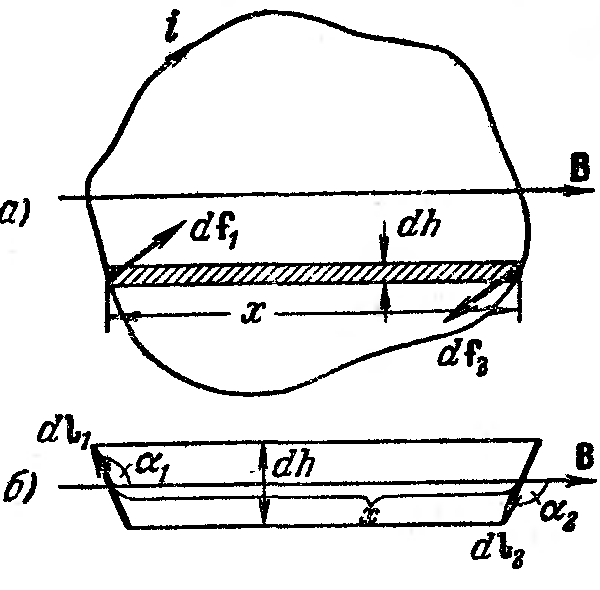
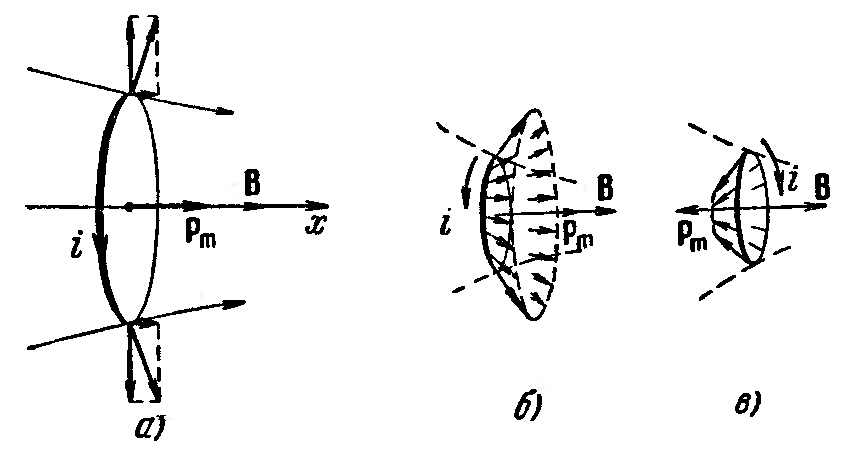
Теперь рассмотрим плоский контур с током в неоднородном магнитном поле. Для простоты будем вначале считать контур круговым. Предположим, что поле изменяется быстрее всего в направлении х, совпадающем с направлением В в том месте, где расположен центр контура, и что магнитный момент контура ориентирован вдоль поля (рис 91,а).
Рис. 91. |
С помощью выражения (48.6) для энергии контура в магнитном поле легко найти количественное выражение для f. Если ориентация магнитного момента по отношению к полю остается неизменной ( = const), то W будет зависеть только от х (через В). Дифференцируя W по х и изменяя у результата знак, получим проекцию силы на ось х
![]()
По предположению в других направлениях поле изменяется слабо, поэтому проекциями силы на другие оси можно пренебречь и считать, что f = fx. Итак,
![]() (48.8)
(48.8)
Согласно полученной нами формуле сила, действующая на контур с током в неоднородном магнитном поле, зависит от ориентации магнитного момента контура относительно направления поля. Если векторы pm и В совпадают по направлению ( = 0), сила положительна, т.е. направлена в сторону возрастания В ( предполагается положительным; в противном случае знак и направление силы изменятся на противоположные, но сила по-прежнему будет втягивать контур в область сильного поля). Если pm и В антипараллельны ( = ), сила отрицательна, т. е. направлена в сторону убывания В.
Этот результат мы уже получили качественно с помощью рис. 91.
Разумеется, кроме силы (48.8) на контур с током в неоднородном магнитном поле будет действовать также вращательный момент (48.3 М = pm В).