С пособы соединения элементов в теории надежности

Существует понятие структурной схемы, из нее необходимо сделать структурно-надежную схему, которая определяет надежность функционирования во времени.

Последовательное соединение (безизбыточная система):

I,II – Полюса

Характеризуется тем, что отказ для любого элемента приводит к отказу системы.

- интенсивность отказов i-шош элемента.

- интенсивность отказа системы

- наработка на отказ системы

- вероятность безотказного функционирования системы, если элементы независимы

- если число восстановительных органов достаточно, т.е. как только отказ появляется, за него сразу «берутся».

Параллельное соединение (избыточная система):

000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000

Горячий резерв.

Дублированная пара

В общем случае:

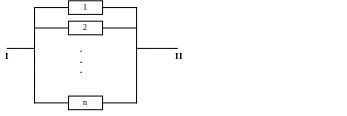
Для дублированной пары:

Q = Q1*Q2 – вероятность отказа

P = 1-Q = 1-(1-P1)(1-P2) – вероятность безотказного функционирования

Kr = (1-(1-Kr1)(1-Kr2)) – коэффициент готовности в случае неограниченных возможностей по восстановлению.

Про и Т нельзя ничего сказать.

Говорим о кратности резервирования. Если n элементов, то (n-1) кратное резервирование.

Скользящий резерв:

Холодный резерв:

Параллельно-Последовательное соединение:

I,II,III – фрагменты с чисто параллельными элементами

-безотказное функционирование фрагмента I

Qi = 1 – Pi, i = 1,2,3 – Вероятность отказа i-ого звена

i=4,5

i=6,7,8

Переходим к структуре:

Pc = PI PII PIII – Вероятность безотказного функционирования системы

Последовательно-параллельная структура

II

Перейдем к структуре:

- вероятность безотказной работы всей системы

Пример схемы, не сводящейся к 4ем классическим соединениями.

Схема «мостик» -структурно-сложная схема.

Попытаемся перейти к последовательно-параллельной схеме:

Однако здесь присутствуют зависимые элементы!!!

Это не классическое паралелльное соединение. В классике все элементы независимы.

Мажоритарная схема:

* - решающий орган для цветов. Его можно убрать.

Мажоритарная система:

! Но на выходе – сигнал по принципу 2 из 3х.(результат совпадает)

Это тоже не сводится к классическому параллельному соединению.

Нужны свои методы расчета.

Рассмотрим:

Структура аппаратно-программного комплекса (апк)

Будем оценивать надежность по структурному критерию.

Классические структуры:

1. Возьмем МКМД (Много команд много данных). Несколько вариантов машин работают автономно.

2. Далее идет конвейерный принцип.

- Конвейерная структура многопрофильной системы

3. Векторная структура

4. Кольцо

5. Звезда

6. Двумерная решетка

7. Рекуррентные структура (по Ушакову)

В надежности в качестве модели исследуется графовая модель.

Существует понятие ориентированных и не ориентированных графов

1. Односвязный ориентированный граф = конвейер

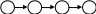
2. Неориентированный граф = вектор

3. Полносвязный ориентированный граф (каждый с каждым)

Нарисуем двумерную решетку в графовой модели:

1

Это многосвязный граф. Т.о. теория графов (графовые модели) является заменой структурных представлений.

Если рассмотреть сети, то их нельзя просто взять графовой моделью!

Любую структуру можно представить графом.

Рассмотрим матрицу связности:

Т.е. сети нельзя оценить показателем надежности – используют 2х мерную матрицу связности.

Для 2х точек сети можно построить грфовую модель, а для всей сети – сложно.

Для иерархической среды также будем рассматривать графовую модель:

Н апример, дерево:

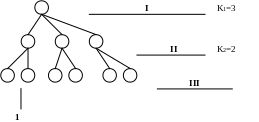
Здесь существуют определенные уровни иерархии. Уровни иерархии бывают изотропные и не изотропные.

Чтобы система была изотропная, показатели надежности должны быть одинаковые у элементов одного уровня.

У каждого уровня существует коэффициент ветвления.

Чтобы система была изотропная, коэффициенты ветвления должны быть одинаковы на каждом уровне (у элементов).

Система 1 представляется двухполюсным графом. Структура может быть от односвязного до полносвязного.

Если такая структура односвязная, то говорят, что это дерево.

Чтобы система была изотропная, структура всех ветвей должна быть одинаковая. Во всех остальных ситуациях система не изотропная.

Звезда так представляется (частный случай изотропной иерархической структуры).

Это не классическая структура. Иерархические структуры в случае введения в них информационной избыточности к двухполюсникам не сводятся.

Рассмотрим: