22. Линейные преобразования. Свойства.

Ортогональные операторы

Линейный оператор называется ортогональным, если

Для того чтобы оператор был ортогональным, необходимо и достаточно, чтобы его матрица в ортонормированном базисе была ортогональной.

Ортогональные операторы и только они сохраняют длину вектора, т. е.

Сопряженные операторы

Оператор называется сопряженным линейному оператору , если

Оператор также является линейным оператором. Если f в некотором ортогональном базисе имеет матрицу A, то в этом базисе оператор имеет матрицу .

Свойства сопряженных операторов: (f - невырожденный).

Самосопряженные операторы

Линейный оператор называется самосопряженным (симметрическим), если

Для самосопряженного оператора

Оператор является самосопряженным тогда и только тогда, когда его матрица в некотором ортонормированном базисе симметрическая.

Свойства самосопряженных операторов: 1) самосопряженный оператор имеет только действительные собственные числа; 2) всякий самосопряженный оператор является оператором простой структуры; 3) для всякого самосопряженного оператора существует ортонормированный базис, состоящий из собственных векторов этого оператора.

23. Нахождение матрицы линейного преобразования.

Пусть в n- мерном линейном пространстве с базисом , ,…, задано линейное преобразование А. Тогда векторы А ,А ,…,А - также векторы этого пространства и их можно представить в виде линейной комбинации векторов базиса:

A = a₁₁ + a₂₁ +…+ a_n1

A = a₁₂ + a₂₂ +…+ a_n2

……………………………….

A = a_n1 + a_n2 +…+ a_nn

Тогда матрица А = называется матрицей линейного преобразования А.

Если в пространстве L взять вектор , то A Î L.

, где

……………………………..

Эти равенства можно назвать линейным преобразованием в базисе , ,…, .

В матричном виде:

, А× ,

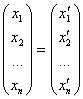24. Ранг и дефект линейного преобразования.

Пусть A — матрица размера над полем C (или R). Пусть T — линейное преобразование, соответствующее A в стандартном базисе; это значит, что T(x) = Ax. Ранг матрицы A — это размерность области значений преобразования T.

Ядро оператора: - множество, обозначаемое Ker f:

Область значений (образ) оператора - множество, обозначаемое Im f:

Множества Ker f и Im f являются подпространствами пространства V.

Ранг оператора (обозначение: dim Im f) - ранг матрицы A линейного оператора f,

dim Im f = rank A.

Дефектом оператора называют dim Ker f,

dim Im f + dim Ker f = n.

2 5. Определение, геометрическая интерпретация и формы записи комплексного числа.

Комплексным числом z будем называть упорядоченную пару действительных чисел x, y записанную в форме z = x + iy, где i- новый объект ("мнимая единица"), для которого при вычислениях полагаем i2 = -1.

Первая компонента комплексного числа z, действительное число x, называется действительной частью числа z, это обозначается так: x = Re z; вторая компонента, действительное число y, называется мнимой частью числа z: xy = Im z.

Геометрически комплексное число z = x + iy изображается как точка с координатами ( x, y) на плоскости. Плоскость, на которой изображаются комплексные числа, называется комплексной плоскостью С.

Тригонометрическая форма комплексного числа. Запись комплексного числа в виде z = x + iy называется алгебраической формой комплексного числа. Изобразим число z как точку на плоскости с декартовыми координатами x, y. Если теперь перейти к полярным координатам , то , поэтому . Угол называется аргументом комплексного числа z и обозначается : . Аргумент комплексного числа определён неоднозначно (с точностью до слагаемых, кратных ): если, например, , то значения , равные и т.д. тоже будут соответствовать числу z; значение аргумента, удовлетворяющее условиям , называют главным; для обозначения всех значений аргумента комплексного числа z применяется символ : .

Показательная форма комплексного числа. Ряд Маклорена для функции сходится к функции при любом действительном х. Формально запишем это разложение для :

Степени числа i: i 2 = -1; i 3 = i 2 i = - i ; i 4 = i 2 i 2 = 1 ; i 5 = i 4 i = i ; i 6 = i 2 = -1; далее значения степеней повторяются (для отрицательных степеней это тоже справедливо: i -1 = - i ; i - 2 = -1; i - 3 = i ; i -4 = 1 ; и т.д.). Поэтому . В круглых скобках стоят ряды для и , которые сходятся для любого действительного ; поэтому получаем . Эта формула называется формулой Эйлера. Теперь любое комплексное число можно представить как ; эта форма записи называется показательной.

26. Операции над комплексными числами.

Два комплексных числа z1 = x1 + iy1 и z2 = x2 + iy2 равны тогда и только тогда, когда равны их действительные и мнимые части: .

Множество комплексных чисел неупорядочено, т.е. для комплексных чисел не вводятся отношения "больше" или "меньше".

Суммой двух комплексных чисел z1 = x1 + iy1 и z2 = x2 + iy2 называется комплексное число z, определяемое соотношением z =(x1 + x2) + (y1 + y2) i, т.е. Re(z1 + z2) = Re z1 + Re z2, Im(z1 + z2) = Im z1 + Im z2.

Это означает, что геометрически комплексные числа складываются как векторы на плоскости, покоординатно.

Произведением двух комплексных чисел z1 = x1 + iy1 и z2 = x2 + iy2 называется комплексное число z, определяемое соотношением z = (x1x2 - y1y2) + (x1y2 + x2y1) i, т.е.

Re(z1 z2) = Re z1 Re z2 – Im z1 Im z2; Im(z1 z2) = Re z1 Im z2 + Im z1 Re z2.

Для нахождения частного комплексных чисел домножим числитель и знаменатель на число, сопряжённое знаменателю: .
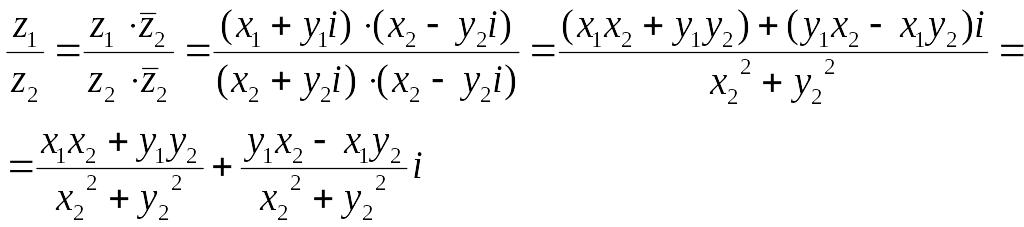